- 在這篇文章內,向量與标量分別用粗體與斜體顯示。例如,位置向量通常用
 表示;而其大小則用
表示;而其大小則用  來表示。四維矢量用加有標號的斜體顯示。例如,
來表示。四維矢量用加有標號的斜體顯示。例如, 或
或 。為了避免歧意,四維矢量的斜體與標號之間不會有括號。例如,
。為了避免歧意,四維矢量的斜體與標號之間不會有括號。例如, 表示
表示 平方;而
平方;而 是
是 的第二個分量。
的第二個分量。
在相對論裏,四維向量(four-vector)是實值四維向量空間裏的矢量。這四維向量空間稱為閔考斯基時空。四維向量的分量分別為在某個時間點與三維空間點的四個數量。在閔考斯基時空內的任何一點,都代表一個「事件」,可以用四維向量表示。從任意慣性參考系觀察某事件所獲得的四維向量,通過勞侖茲變換,可以變換為從其它慣性參考系觀察該事件所獲得的四維向量。
本文章只思考在狹義相對論範圍內的四維向量,儘管四維向量的概念延伸至廣義相對論。在本文章內寫出的一些結果,必須加以修改,才能在廣義相對論範圍內成立。
數學性質[编辑]
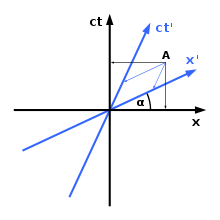 在閔考斯基時空裡,不同慣性參考系的座標軸
在閔考斯基時空裡,不同慣性參考系的座標軸
在閔考斯基時空內的任何一點,都可以用四維向量(一組標準基底的四個坐標)  來表示;其中,上標
來表示;其中,上標  標記時空的維數次序。稱這四維向量為「坐標四維向量」,又稱「四維坐標」,定義為
標記時空的維數次序。稱這四維向量為「坐標四維向量」,又稱「四維坐標」,定義為
 ;
;
其中, 是光速,
是光速, 是時間,
是時間, 是位置的三維直角坐標。
是位置的三維直角坐標。
為了確使每一個坐標的單位都是長度單位,定義  。
。
「四維位移」定義為兩個事件之間的矢量差。在時空圖裏,四維位移可以用從第一個事件指到第二個事件的箭矢來表示。當矢量的尾部是坐標系的原點時,位移就是位置。四維位移  表示為
表示為
 。
。
帶有上標的四維向量  稱為反變矢量,其分量標記為
稱為反變矢量,其分量標記為
 。
。
假若,標號是下標,則稱四維向量  為協變矢量。其分量標記為
為協變矢量。其分量標記為
 。
。
在這裡,閔考斯基度規  被設定為
被設定為
 。
。
採用愛因斯坦求和約定,則四維向量的協變坐標和反變坐標之間的關係為
 。
。
閔考斯基度規與它的「共軛度規張量」  相等:
相等:
 。
。
勞侖茲變換[编辑]
給予兩個慣性參考系  、
、  ;相對於參考系
;相對於參考系  ,參考系
,參考系  以速度
以速度  移動。對於這兩個參考系,相關的「勞侖茲變換矩陣」
移動。對於這兩個參考系,相關的「勞侖茲變換矩陣」  是
是
 ;
;
其中, 是勞侖茲因子,
是勞侖茲因子, 是「貝塔因子」。
是「貝塔因子」。
對於這兩個參考系  、
、  ,假設一個事件的四維坐標分別為
,假設一個事件的四維坐標分別為  、
、  。那麼,這兩個四維坐標之間的關係為
。那麼,這兩個四維坐標之間的關係為
 、
、 ;
;
其中, 是
是  的反矩阵,
的反矩阵,
 。
。
將這兩個四維坐標之間的關係式合併為一,則可得到
 。
。
因此,可以找到勞侖茲變換矩陣的一個特性:
 ;
;
其中, 是克羅內克函數。
是克羅內克函數。
另外一個很有用的特性為
 ;
;
給定一個事件在某慣性參考系的四維坐標,通過勞侖茲變換,就可計算出這事件在另外一個慣性參考系的四維坐標。這是個很有用的物理性質。當研究物理現象時,所涉及的四維向量,最好都能夠具有這有用的性質。這樣,可以使得數學分析更加精緻犀利。以方程式表示,對於兩個參考系  、
、  ,具有這種有用性質的四維向量
,具有這種有用性質的四維向量  、
、 滿足
滿足
 、
、 。
。
在計算這四維向量對於時間的導數時,若能選擇固有時為時間變數,則求得的四維向量仍舊具有這有用的性質。因為,固有時乃是個不變量;改變慣性參考系不會改變不變量。
假設一個物體運動於閔考斯基時空。在「實驗室參考系」裡,物體運動的速度隨著時間改變。對於每瞬時刻,選擇與物體同樣運動的慣性參考系,稱為「瞬間共動參考系」(momentarily comoving reference frame)。在這瞬間共動參考系裡,物體的速度為零,因此,這參考系也是物體的「瞬間靜止參考系」。隨著物體不斷地改變運動速度與方向,新的慣性參考系也會不斷地改換為瞬間共動參考系。[1]:41-42隨著這些不斷改換的瞬間同行坐標系所測得的時間即為固有時,標記為  。這就好像給物體掛戴一隻手錶,隨著物體的運動,手錶也會做同樣的運動,而手錶所紀錄的時間就是固有時。
。這就好像給物體掛戴一隻手錶,隨著物體的運動,手錶也會做同樣的運動,而手錶所紀錄的時間就是固有時。
這物體的運動可以用一條世界線  來描述。由於時間膨脹,發生於物體的兩個本地事件的微小固有時間隔
來描述。由於時間膨脹,發生於物體的兩個本地事件的微小固有時間隔  與從別的慣性參考系
與從別的慣性參考系  所觀測到的微小時間間隔
所觀測到的微小時間間隔  的關係為
的關係為
 。
。
所以,固有時  對於其它時間
對於其它時間  的導數為
的導數為
 。
。
閔考斯基內積[编辑]
在閔考斯基空間裡,兩個四維向量  與
與  的內積,稱為閔考斯基內積,以方程式表示為:
的內積,稱為閔考斯基內積,以方程式表示為:
 。
。
由於這內積並不具正定性,即

可能會是負數;而歐幾里得內積一定不是負數。
許多學者喜歡使用相反正負號的  :
:
 。
。
這樣, 與
與  的內積改變為
的內積改變為
 。
。
其它相聯的量值也會因而改變正負號,但這不會改變系統的物理性質。
從參考系  改換至另一參考系
改換至另一參考系  ,
, 與
與  的內積為
的內積為
 。
。
所以,在閔考斯基時空內,兩個四維向量的內積是個不變量:[1]:44-46
 。
。
四維向量可以分類為類時,類空,或類光(零矢量):
- 類時矢量:
 ,
,
- 類空矢量:
 ,
,
- 類光矢量:
 。
。
動力學實例[编辑]
四維速度[编辑]
設想一個物體運動於閔考斯基時空,則其世界線的任意事件  的四維速度
的四維速度  定義為[1]:46-48
定義為[1]:46-48
 ;
;
其中, 是三維速度,或經典速度矢量。
是三維速度,或經典速度矢量。
 的空間部分與經典速度
的空間部分與經典速度  的關係為
的關係為
 。
。
四維速度與自己的內積等於光速平方,是一個不變量:
 。
。
在物體的瞬間共動參考系裡,物體的速度為零,因此,四維速度為
 ,
,
其方向與瞬間共動參考系的第零個基底向量  同向;
同向;
其中, 表示從瞬間共動參考系觀察得到的數據。
表示從瞬間共動參考系觀察得到的數據。
四維加速度[编辑]
四維加速度  定義為 [1]:46-48
定義為 [1]:46-48
 。
。
經過一番運算,可以得到勞侖茲因子對於時間的導數:
 ;
;
其中, 是經典加速度。
是經典加速度。
所以,四維加速度  可以表示為
可以表示為
 。
。
由於  是個常數,四維加速度與四維速度相互正交;也就是說,四維速度與四維加速度的閔考斯基內積等於零:
是個常數,四維加速度與四維速度相互正交;也就是說,四維速度與四維加速度的閔考斯基內積等於零:
 。
。
對於每一條世界線,這計算結果都成立。
注意到在瞬間共動參考系裡,  只有時間分量不等於零,所以,
只有時間分量不等於零,所以,  為的時間分量為零:
為的時間分量為零:
 。
。
四維動量[编辑]
一個靜止質量為  的粒子的四維動量
的粒子的四維動量  定義為
定義為
 。
。
經典動量  定義為
定義為
 ;
;
其中, 是相對論性質量。
是相對論性質量。
所以, 的空間部分等於經典動量
的空間部分等於經典動量  :
:
 。
。
四維力[编辑]
作用於粒子的四維力定義為粒子的四維動量對於固有時的導數:
 。
。
提出四維動量內的靜止質量因子,即可發覺四維力就是靜止質量乘以四維加速度:
 。
。
因此,四維力可以表示為
 。
。
經典力  定義為
定義為
 。
。
所以, 的空間部分等於
的空間部分等於  :
:
 。
。
物理內涵[编辑]
在四維向量的表述裏,存在著許多能量與物質之間的關係。從這些特別關係,可以顯示出這表述的功能與精緻。
質能方程式[编辑]
假設,在微小時間間隔  ,一個運動於時空的粒子,感受到作用力
,一個運動於時空的粒子,感受到作用力  的施加,而這粒子的微小位移為
的施加,而這粒子的微小位移為  。那麼,作用力
。那麼,作用力  對於這粒子所做的微小機械功
對於這粒子所做的微小機械功  為
為
 。
。
因此,這粒子的動能的改變  為
為
 。
。
粒子的動能  對於時間的導數為
對於時間的導數為
 。
。
將前面經典力和經典速度的公式帶入,可以得到
 。
。
這公式的反微分為
 。
。
當粒子靜止時,動能等於零。所以,
 。
。
這公式的右手邊第二個項目就是靜止能量  。動能
。動能  加上靜止能量
加上靜止能量  等於總能量
等於總能量  :
:
 。
。
再加簡化,以相對論性質量  表示:
表示:
 。
。
這方程式稱為質能方程式。
能量-動量關係式[编辑]
使用質能方程式  ,四維動量可以表示為
,四維動量可以表示為
 。
。
四維動量與自己的內積為
 。
。
改以四維速度來計算內積:
 。
。
所以,能量-動量關係式為
 。
。
電磁學實例[编辑]
四維電流密度[编辑]
在電磁學裏,四維電流密度  是一個四維向量,定義為
是一個四維向量,定義為
 ;
;
其中, 是電荷密度,
是電荷密度, 是三維電流密度。
是三維電流密度。
在瞬間共動參考系所觀測到的電荷密度,稱為固有電荷密度  。四維電流密度與四維速度的關係為
。四維電流密度與四維速度的關係為
 。
。
電荷守恆定律能以三維矢量表示為
 。
。
這定律也能以四維電流密度表示為
 。
。
從這方程式,可以推論四維電流密度的四維散度等於零。
電磁四維勢[编辑]
電磁四維勢是由電勢  與矢量勢
與矢量勢  共同形成的,定義為
共同形成的,定義為
 。
。
黎曼-索末菲方程式表示電磁四維勢與四維電流密度之間的關係[2]:
 ;
;
其中, 是磁常數,
是磁常數, 是達朗貝爾算符,又稱為四維拉普拉斯算符。
是達朗貝爾算符,又稱為四維拉普拉斯算符。
四維頻率和四維波矢量[编辑]
一個平面電磁波的四維頻率  定義為
定義為
 ;
;
其中, 是電磁波的頻率,
是電磁波的頻率, 是朝著電磁波傳播方向的單位矢量。
是朝著電磁波傳播方向的單位矢量。
四維頻率與自己的內積永遠等於零:
 。
。
一個近單色光的波包的波動性質可以用四維波矢量  來描述:
來描述:
 。
。
其中, 是三維波矢量。
是三維波矢量。
四維波矢量與四維頻率之間的關係為
 。
。
參考文獻[编辑]
|
|---|
| | | | 基礎概念 | |
|---|
| | 现象 | |
|---|
| | 時空 | |
|---|
| | 運動學 | |
|---|
| | 動力學 | |
|---|
| | 歷史背景 | |
|---|
| | 科學家 | |
|---|
| | 相關理論方法 | |
|---|
|














































































































































