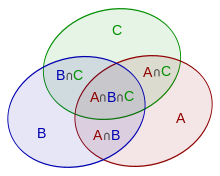
三個集的情況 容斥原理 (inclusion-exclusion principle)又称排容原理 ,在組合數學 裏,其說明若
A
1
{\displaystyle A_{1}}
A
n
{\displaystyle A_{n}}
有限集 ,則
|
⋃
i
=
1
n
A
i
|
=
∑
i
=
1
n
|
A
i
|
−
∑
1
≤
i
<
j
≤
n
|
A
i
∩
A
j
|
+
∑
1
≤
i
<
j
<
k
≤
n
|
A
i
∩
A
j
∩
A
k
|
−
⋯
+
(
−
1
)
n
−
1
|
A
1
∩
⋯
∩
A
n
|
.
{\displaystyle {\begin{aligned}\left|\bigcup _{i=1}^{n}A_{i}\right|={}&\sum _{i=1}^{n}|A_{i}|-\sum _{1\leq i<j\leq n}|A_{i}\cap A_{j}|+\sum _{1\leq i<j<k\leq n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.\end{aligned}}}
其中
|
A
|
{\displaystyle |A|}
A
{\displaystyle A}
基數 。例如在兩個集的情況時,我們可以通過將
|
A
|
{\displaystyle |A|}
|
B
|
{\displaystyle |B|}
交集 的基數,而得到其并集 的基數。
两个集合的容斥原理 [ 编辑 ] n(A∪B)=n(A)+n(B) -n(A∩B)
三个集合的容斥原理 [ 编辑 ] |A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|
n个集合的容斥原理 [ 编辑 ] 要计算几个集合并集的大小,我们要先将所有单个集合 的大小计算出来,然后减去所有两个集合相交 的部分,再加回所有三个集合相交 的部分,再减去所有四个集合相交 的部分,依此类推,一直计算到所有集合相交 的部分。
最终得到公式:
|
⋃
i
=
1
n
A
i
|
=
∑
i
=
1
n
|
A
i
|
−
∑
1
≤
i
<
j
≤
n
|
A
i
∩
A
j
|
+
∑
1
≤
i
<
j
<
k
≤
n
|
A
i
∩
A
j
∩
A
k
|
−
⋯
+
(
−
1
)
n
−
1
|
A
1
∩
⋯
∩
A
n
|
.
{\displaystyle {\begin{aligned}\left|\bigcup _{i=1}^{n}A_{i}\right|={}&\sum _{i=1}^{n}|A_{i}|-\sum _{1\leq i<j\leq n}|A_{i}\cap A_{j}|+\sum _{1\leq i<j<k\leq n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.\end{aligned}}}
又可写成
|
⋃
i
=
1
n
A
i
|
=
∑
k
=
1
n
(
−
1
)
k
+
1
(
∑
1
≤
i
1
<
⋯
<
i
k
≤
n
|
A
i
1
∩
⋯
∩
A
i
k
|
)
{\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leq i_{1}<\cdots <i_{k}\leq n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)}
或
|
⋃
i
=
1
n
A
i
|
=
∑
∅
≠
J
⊆
{
1
,
2
,
…
,
n
}
(
−
1
)
|
J
|
−
1
|
⋂
j
∈
J
A
j
|
.
{\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}}(-1)^{|J|-1}{\Biggl |}\bigcap _{j\in J}A_{j}{\Biggr |}.}
概率论中的容斥原理 [ 编辑 ] 在概率论 中,对于概率空间
(
Ω
,
F
,
P
)
{\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}
A 1 ,……,A n n = 2时容斥原理的公式为:
P
(
A
1
∪
A
2
)
=
P
(
A
1
)
+
P
(
A
2
)
−
P
(
A
1
∩
A
2
)
,
{\displaystyle \mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),}
当n = 3时,公式为:
P
(
A
1
∪
A
2
∪
A
3
)
=
P
(
A
1
)
+
P
(
A
2
)
+
P
(
A
3
)
−
P
(
A
1
∩
A
2
)
−
P
(
A
1
∩
A
3
)
−
P
(
A
2
∩
A
3
)
+
P
(
A
1
∩
A
2
∩
A
3
)
{\displaystyle \mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})}
一般地:
P
(
⋃
i
=
1
n
A
i
)
=
∑
i
=
1
n
P
(
A
i
)
−
∑
i
,
j
:
i
<
j
P
(
A
i
∩
A
j
)
+
∑
i
,
j
,
k
:
i
<
j
<
k
P
(
A
i
∩
A
j
∩
A
k
)
−
⋯
+
(
−
1
)
n
−
1
P
(
⋂
i
=
1
n
A
i
)
,
{\displaystyle \mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{i=1}^{n}\mathbb {P} (A_{i})-\sum _{i,j\,:\,i<j}\mathbb {P} (A_{i}\cap A_{j})+\sum _{i,j,k\,:\,i<j<k}\mathbb {P} (A_{i}\cap A_{j}\cap A_{k})-\ \cdots \ +(-1)^{n-1}\,\mathbb {P} {\biggl (}\bigcap _{i=1}^{n}A_{i}{\biggr )},}
也可以写成:
P
(
⋃
i
=
1
n
A
i
)
=
∑
k
=
1
n
(
−
1
)
k
−
1
∑
I
⊂
{
1
,
…
,
n
}
|
I
|
=
k
P
(
A
I
)
,
{\displaystyle \mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}(-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,n\} \atop \scriptstyle |I|=k}\mathbb {P} (A_{I}),}
对于一般的测度空间 (S ,Σ ,μ )和有限测度的可测 子集A 1 ,……,An ,上面的恒等式也成立,如果把概率测度
P
{\displaystyle \mathbb {P} }
μ 。
特殊情况 [ 编辑 ] 如果在容斥原理的概率形式中,交集AI 的概率只与I 中元素的个数有关,也就是说,对于{1, ..., n }中的每一个k ,都存在一个ak ,使得:
a
k
=
P
(
A
I
)
{\displaystyle a_{k}=\mathbb {P} (A_{I})}
I
⊂
{
1
,
…
,
n
}
(
|
I
|
=
k
)
,
{\displaystyle I\subset \{1,\ldots ,n\}\,\,(|I|=k),}
则以上的公式可以简化为:
P
(
⋃
i
=
1
n
A
i
)
=
∑
k
=
1
n
(
−
1
)
k
−
1
(
n
k
)
a
k
{\displaystyle \mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}}
这是由于二项式系数
(
n
k
)
{\displaystyle \scriptstyle {\binom {n}{k}}}
类似地,如果对有限集合A 1 ,……,An 的并集的元素个数感兴趣,且对于{1, ..., n }中的每一个k ,交集
A
I
:=
⋂
i
∈
I
A
i
{\displaystyle A_{I}:=\bigcap _{i\in I}A_{i}}
的元素个数都相同,例如ak = |AI |,与{1, ..., n }的k 元素子集I 无关,则:
|
⋃
i
=
1
n
A
i
|
=
∑
k
=
1
n
(
−
1
)
k
−
1
(
n
k
)
a
k
.
{\displaystyle {\biggl |}\bigcup _{i=1}^{n}A_{i}{\biggr |}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}\,.}
在一般的测度空间(S ,Σ ,μ )和有限测度的可测子集A 1 ,……,An 的情况中,也可以进行类似的简化。
容斥原理的证明 [ 编辑 ] 欲证明容斥原理,我们首先要验证以下的关于指示函数 的等式:
1
∪
i
=
1
n
A
i
=
∑
k
=
1
n
(
−
1
)
k
−
1
∑
I
⊂
{
1
,
…
,
n
}
|
I
|
=
k
1
A
I
(
∗
)
{\displaystyle 1_{\cup _{i=1}^{n}A_{i}}=\sum _{k=1}^{n}(-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,n\} \atop \scriptstyle |I|=k}1_{A_{I}}\qquad (*)}
至少有两种方法来证明这个等式:
第一种方法 我们只需证明对于A 1 ,……,An 的并集中的每一个x ,等式都成立。假设x 正好属于m 个集合(1 ≤ m ≤ n ),不妨设它们为A 1 ,……,Am 。则x 处的等式化为:
1
=
∑
k
=
1
m
(
−
1
)
k
−
1
∑
I
⊂
{
1
,
…
,
m
}
|
I
|
=
k
1.
{\displaystyle 1=\sum _{k=1}^{m}(-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,m\} \atop \scriptstyle |I|=k}1.}
m 元素集合中的k 元素子集的个数,是二项式系数
(
m
k
)
{\displaystyle \textstyle {\binom {m}{k}}}
1
=
(
m
0
)
{\displaystyle \textstyle 1={\binom {m}{0}}}
(
m
0
)
=
∑
k
=
1
m
(
−
1
)
k
−
1
(
m
k
)
.
{\displaystyle {\binom {m}{0}}=\sum _{k=1}^{m}(-1)^{k-1}{\binom {m}{k}}.}
把所有的项移到等式的左端,我们便得到(1 – 1)m x 成立。
第二种方法 设A 表示集合A 1 ,……,An 的并集。于是:
0
=
(
1
A
−
1
A
1
)
(
1
A
−
1
A
2
)
⋯
(
1
A
−
1
A
n
)
,
{\displaystyle 0=(1_{A}-1_{A_{1}})(1_{A}-1_{A_{2}})\cdots (1_{A}-1_{A_{n}})\,,}
这是因为对于不在A 内的x ,两边都等于零,而如果x 属于其中一个集合,例如Am ,则对应的第m 个因子为零。把右端的乘积展开来,便可得到等式(*)。
归纳法证明 [ 编辑 ] 设:S1 = n (A1 )+n (A2 )+n (A3 ) +…...+n (An )
S2 = n(A1 ∩A2 )+ n(A1 ∩A3 ) …...+ n(A1 ∩An )+ n(A2 ∩A3 )+ …...+n(An-1 ∩An)
S3 = n(A1 ∩A2 ∩A3 )+ ……+ n(An-2 ∩An-1 ∩An)……
Sn =n(A1 ∩A2 ∩A3 ∩……∩An )
求证:A=n(A1 ∪A2 ∪A3 ∪A4 ……∪An )= S1 -S2 + S3 +……+(-1)n-1 Sn
证明:当n=2时,A=n(A1 ∪A2 )=n(A1 )+n(A2 ) -n(A1 ∩ A2 )= S1 -S2
假设:当n=k(k>=2)时,A=n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak )= S1 -S2 + S3 +……+(-1)k-1 Sk 等式成立。
当n=k+1时,
A= n( (A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) ∪Ak+1 )
= n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak )+n(Ak+1 )-n((A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) ∩Ak+1 )
= n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) +n(Ak+1 )-n((A1 ∩Ak+1 ) ∪(A2 ∩Ak+1 ) ∪(A3 ∩Ak+1 ) ∪ …∪(Ak ∩Ak+1 ))
∵ 当n=k时,等式成立
∴A= n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) +n(Ak+1 )-(n (A1 ∩Ak+1 )+ n (A2 ∩Ak+1 )+ ……+n(Ak ∩Ak+1 )-n(A1 ∩A2 ∩Ak+1 )-n(A1 A3 ∩Ak+1 ) -……- n(Ak-1 ∩Ak ∩Ak+1 )+ ……+(-1)k .n(A1 ∩A2 ∩A3 ∩∪……∩Ak+1 )
= S1 -S2 + S3 +……+(-1)k-1 Sk +n(Ak+1 )-(n (A1 ∩Ak+1 )+ n (A2 ∩Ak+1 )+ ……+n(Ak ∩Ak+1 )-n(A1 ∩A2 ∩Ak+1 )-n(A1 ∩A3 ∩Ak+1 ) -……- n(Ak-1 ∩Ak ∩Ak+1 )+ ……+(-1)k .n(A1 ∩A2 ∩A3 ∩∪……∩Ak+1 )
= S1 -S2 + S3 +……+(-1)k Sk+1
综上所述,当n>=2时,n (A1 ∪A2 ∪A3 ∪A4 ……∪An )
= n (A1 )+n (A2 )+n (A3 ) ……+ n (An )-n(A1 ∩A2 )- n(A1 ∩A3 ) ……- n(A1 ∩An )- n(A2 ∩A3 )- ……-n(An-1 ∩An)+n(A1 ∩A2 ∩A3 )+ n(A1 ∩A2 ∩A3 )+ ……+ n(An-2 ∩An-1 ∩An)- ……+……+(-1)n-1 .n(A1 ∩A2 ∩A3 ∩……∩An )[1]
其它形式 [ 编辑 ] 有时容斥原理用以下的形式来表述:如果
g
(
A
)
=
∑
S
:
S
⊆
A
f
(
S
)
{\displaystyle g(A)=\sum _{S\,:\,S\subseteq A}f(S)}
那么:
f
(
A
)
=
∑
S
:
S
⊆
A
(
−
1
)
|
A
|
−
|
S
|
g
(
S
)
{\displaystyle f(A)=\sum _{S\,:\,S\subseteq A}(-1)^{\left|A\right|-\left|S\right|}g(S)}
在这种形式中可以看出,它是A 的所有子集的偏序集合 的指标代数 的莫比乌斯反演公式 。
在许多情况下,容斥原理都可以给出精确的公式(特别是用埃拉托斯特尼筛法 计算素数 的个数时),但是用处不大,这是因为它里面含有的项太多。即使每一个单独的项都可以准确地估计,误差累积起来仍然意味着容斥原理不能直接应用。在数论 中,这个困难由维戈·布朗 解决。开始时进展很慢,但他的想法逐渐被其他数学家所应用,于是便产生了许多各种各样的筛法 。这些方法是尝试找出被“筛选”的集合的上界,而不是一个确切的公式。
容斥原理的一个著名的应用,是计算一个有限集合的所有乱序 排列的数目。一个集合A 的错排 ,是从A 到A 的没有不动点的双射 。通过容斥原理,我们可以证明,如果A 含有n 个元素,则乱序排列的数目为[n ! / e ],其中[x ]表示最接近x 的整数。
这也称为n 的子阶乘 ,记为!n 。可以推出,如果所有的双射都有相同的概率,则当n 增大时,一个随机双射是错排的概率迅速趋近于1/e 。
交集的计算 [ 编辑 ] 容斥原理与德·摩根定理 结合起来,也可以用于计算集合的交集中元素的数目。设
A
¯
k
{\displaystyle \scriptstyle {\overline {A}}_{k}}
A k A 的补集 ,使得对于每一个k ,都有
A
k
⊆
A
{\displaystyle \scriptstyle A_{k}\,\subseteq \,A}
⋂
i
=
1
n
A
i
=
⋃
i
=
1
n
A
¯
i
¯
{\displaystyle \bigcap _{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A}}_{i}}}}
这样便把计算交集的问题化为计算并集的问题。
拓展阅读 [ 编辑 ] 参考文献 [ 编辑 ] 本條目含有来自PlanetMath 《principle of inclusion-exclusion 》的內容,版权遵守知识共享协议:署名-相同方式共享 协议 。