摩尔型有限状态机
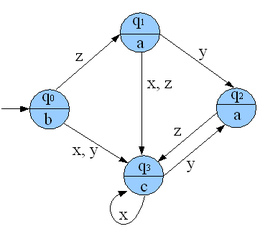
在计算理论中,摩尔型有限状态机(英語:Moore machine)是指输出只由当前的状态所确定的有限状态自动机。摩尔型有限状态机的状态图对每个状态包含一个输出信号,相对于米利型有限状态机,它映射机器中的“转移”到输出。
摩尔型有限状态机的名字来自它的提出者,写了《Gedanken-experiments on Sequential Machines》的状态机先驱愛德華·F·摩爾。[1]
運作機制[编辑]
多数数字电子系统被设计为时序系统。时序系统是受限制形式的摩尔型有限状态机,它的状态只在全局时钟信号改变的时候改变。当前状态典型的存储在触发器中,而全局时钟信号连接到触发器的“时钟”输入上。时序系统是解决亚稳定性问题的一种方法。典型的摩尔型有限状态机包括组合逻辑链来把当前状态解码为输出(lambda)。当前状态一旦改变,这种改变通过这些链传播,几乎立即导致输出改变(或不改变)。有确保在这些变化在沿着链传播这段短暂时期在输出上不出现glitch的技术,但是设计出的大多数系统都忽略在短暂的转移时间的冒险。输出接着停留同样不确定(LED保持点亮,电力保持连接到电机等等),直到摩尔机再次改变状态。
摩尔型有限状态机的输出只与有限状态自动机的当前状态有关,与输入信号的当前值无关。摩尔型有限状态机在时钟脉冲的有效边沿后的有限个门延后,输出达到稳定值。即使在一个时钟周期内输入信号发生变化,输出也会在一个完整的时钟周期内保持稳定值而不变。输入对输出的影响要到下一个时钟周期才能反映出来。摩尔型有限状态机最重要的特点就是将输入与输出信号隔离开来。
形式定义[编辑]
摩尔机形式定义为6-元组{ S, S0, Σ, Λ, T, G },构成如下:
- 状态的有限集合(S)
- 开始状态(也叫做初始状态)S0,它是S的元素
- 叫做输入字母表的有限集合(Σ)
- 叫做输出字母表的有限集合(Λ)
- 映射状态和输入到下一个状态的转移函数(T : S × Σ → S)
- 输出函数(G : S → Λ)映射每个状态到输出字母表
在摩尔机中的状态的数目大于等于在对应的Mealy机中状态的数目。
参见[编辑]
引用[编辑]
註釋[编辑]
- ^ Moore, Edward F. Gedanken-experiments on Sequential Machines. Automata Studies,Annals of Mathematical Studies (Princeton, N.J.: Princeton University Press). 1956, (34): 129–153.
參考文獻[编辑]
- Moore E. F. Gedanken-experiments on Sequential Machines. Automata Studies, Annals of Mathematical Studies, 34, 129–153. Princeton University Press, Princeton, N.J.(1956)。
- Karatsuba A. A. Solution of one problem from the theory of finite automata. Usp. Mat. Nauk, 15:3, 157–159(1960)。
- Karacuba A. A. Experimente mit Automaten (German) Elektron. Informationsverarb. Kybernetik, 11, 611–612(1975)。
- Karatsuba A. A. List of research works (页面存档备份,存于互联网档案馆)
| |||||||||||||||||
