梯形公式

線性函數（紅色）會作用估算函數$f(x)$ （藍色）。

在數學裏，梯形公式是用作估算定積分

$\int_{a}^{b} f(x)\,dx.$

梯形公式會把函數圖像$f(x)$當作成梯形並估算它的面積。以下就是估算所用的公式

$\int_{a}^{b} f(x)\, dx \approx (b-a)\frac{f(a) + f(b)}{2}.$

梯形公式

每一區間相同

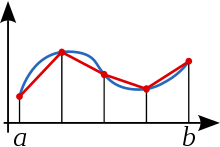梯形公式的示意圖（長度相同的區間）。

為了計算出更加準確的定積分，可以把積分的區間$[a, b]$分成$N$份，當中$N$趨向無限，分割出的每一個區間長度必定要是一樣的，然後就可以應用梯形公式：

$\int_a^b f(x)\,dx \approx \frac{b-a}{N} \left[ {f(a) + f(b) \over 2} + \sum_{k=1}^{N-1} f \left( a+k \frac{b-a}{N} \right) \right].$

亦可以寫成：

$\int_a^b f(x)\,dx \approx \frac{b-a}{2N} \left(f(x_0) + 2f(x_1) + 2f(x_2)+\cdots+2f(x_{N-1}) + f(x_N) \right)$

當中

$x_k=a+k \frac{b-a}{N},\text{ for }k=0, 1, \dots, N$

當區間的長度並不相同時，這一條公式便不能使用。

每一區間並不相同

梯形公式的示意圖（長度不相同的區間）

給予$x_1,\ldots,x_N$以及$y_1,\ldots,y_N$，定積分就可以估算成

$\int_a^b f(x)\,dx \approx \frac{1}{2} \sum_{i=2}^{N} (x_i-x_{i-1})(y_i+y_{i-1})$,

當中

$y_i=f(x_i)$.

誤差分析

應用梯形公式的誤差值是真值數字與運用梯形公式結果的差異：

$\text{error} = \int_a^b f(x)\,dx - \frac{b-a}{N} \left[ {f(a) + f(b) \over 2} + \sum_{k=1}^{N-1} f \left( a+k \frac{b-a}{N} \right) \right]$

如果a 至 b 中存在一個實數ξ，那麼

$\text{error} = -\frac{(b-a)^3}{12N^2} f''(\xi)$

如果被積函數是一個凸函數（亦即有一個正值二階導數），那麼誤差會是一個負數，也代表梯形公式的估算值高估了真實數字。這可以利用一個幾何圖形代去表達：梯形不但覆蓋曲線下的面積更超越其範圍。同樣地，如果被積函數是一個凹函數，梯形公式就會低估其真實數字因為曲線下部份面積沒有被計算在內。如果被積函數中有拐點。它的錯誤是比較難去估計。

一般而言有數種方法可以去分析誤差，例如是：傅利葉級數。

在N → ∞的情況下，趨向性的估計誤差是：

$\text{error} = -\frac{(b-a)^2}{12N^2} \big[ f'(b)-f'(a) \big] + O(N^{-3}).$