正圖形列表
| 正多邊形(二維) | |
|---|---|
| 凸 | 星形 |
 {5} |
 {5/2} |
| 正多面體(三維) | |
| 凸 | 星形 |
 {5,3} |
 {5/2,5} |
| 正鑲嵌圖(二維) | |
| 平面 | 雙曲 |
 {4,4} |
 {5,4} |
| 正多胞體(四維) | |
| 凸 | 星形 |
 {5,3,3} |
 {5/2,5,3} |
| 正堆砌體(三維) | |
| 平面 | 雙曲 |
 {4,3,4} |
 {5,3,4} |
此頁面列出了所有的歐幾里得空間、雙曲空間和球形空間的正圖形或正多胞形。施萊夫利符號可以描述每一個正圖形或正多胞形,他被廣泛使用如下面的每一個緊湊的參考名稱。
正圖形或正多胞形可由其維度分類,也可以分成凸、非凸(星形、扭歪、複合或凹)和無窮等形式。非凸形式(或凹形式)使用與凸形式相同的頂點,但面(或邊)有相交。無限的形式則是在一較低維的歐幾里得空間中密鋪(鑲嵌或堆砌)。
無限的形式可以擴展到密鋪雙曲空間。雙曲空間是和正常的空間有相同的規模,但平行線在一定的距離內會分岔得越來越遠。這使得頂點值可以存在負角度的缺陷,例如製作一個由個正三角形組成的頂點,它們可以被平放。它不能在普通平面上完成的,但可以在一個雙曲平面上構造。
概觀[编辑]
請注意,平面密鋪和雙曲密鋪的維數比預期多一維。這是因為它們是有限多胞形在不同維度的類比:凸正n胞形可以看作(n−1)維球面空間的鑲嵌。因此,歐幾里德平面的三個正鑲嵌圖(正三角形鑲嵌、正方形鑲嵌和正六邊形鑲嵌)列在第三維度而不是第二維下。
| 有限[註 1] | 平面[註 2] | 雙曲[註 3] | 複合[註 4] | 抽象 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 維度 | 凸 | 非凸 | 密鋪 | |||||||||||||||
| 星形 | 扭歪 | 凸 | 星形 | 扭歪 | 緊湊 | 仿緊 | 非緊 | |||||||||||
| 凸 | 星形 | 凸 | 凸 | 星形 | ||||||||||||||
| -1[註 5] | 0 | 0 | 0 | 0 | 0[註 6] | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1[註 7] | |||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||
| 1 | 1 | 0 | 0 | 1[註 8] | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||
| 2 | ∞ | ∞ | ∞ | 1 | 1 | 1 | 0 | 0 | 0 | ∞ | ∞ | ∞ | ||||||
| 3 | 5 | 4 | ? | 3 | 3 | ∞ | ∞ | ∞ | ∞ | 5 | 0 | ∞ | ||||||
| 4 | 6 | 10 | ? | 1 | ? | 4 | 0 | 11 | ∞ | 26 | 20 | ∞ | ||||||
| 5 | 3 | 0 | ? | 3 | ? | 5 | 4 | 2 | 186[1] | 0 | 0 | ∞ | ||||||
| 6 | 3 | 0 | ? | 1 | ? | 0 | 0 | 5 | 66[1] | 0 | 0 | ∞ | ||||||
| 7 | 3 | 0 | ? | 1 | ? | 0 | 0 | 0 | 36[1] | 3 | 0 | ∞ | ||||||
| 8 | 3 | 0 | ? | 1 | ? | 0 | 0 | 0 | 13[1] | 6 | 0 | ∞ | ||||||
| 9 | 3 | 0 | ? | 1 | ? | 0 | 0 | 0 | 10[1] | 0 | 0 | ∞ | ||||||
| 10 | 3 | 0 | ? | 1 | ? | 0 | 0 | 0 | 8[1] | 0 | 0 | ∞ | ||||||
| 11 | 3 | 0 | ? | 1 | ? | 0 | 0 | 0 | 4[1] | 0 | 0 | ∞ | ||||||
| 12+ | 3 | 0 | ? | 1 | ? | 0 | 0 | 0 | [2] | ≤2[註 9] | 0 | ∞ | ||||||
| ||||||||||||||||||
零維或以下的正圖形[编辑]

在維數為零的空間能存在的多胞形只有點[3],無法有其他幾何或拓樸組合,而维數比零更低則是在抽象理論中的虛無多胞形(英語:Null polytope)代表一種空集合,在抽象理論中被看作是一種負一維的多胞形[4],但其是一種抽象多胞形。然而,在數學上,零維空間是按以下的不等價定義之一,維數為零的拓撲空間:按覆蓋維數的概念,一個拓撲空間是零維空間,若空間的任何開覆蓋,都有一個加細,使得空間內每一點,都在這個加細的恰好一個開集內;或者按小歸納維數的概念,一個拓撲空間是零維空間,若空間有一個由閉開集組成的基。這兩個概念對可分可度量化空間為等價[5][6]。而負一維空間僅是在抽象理論表示一個比零維多胞形更低維度的一個元詞。
依據正圖形的定義,一個多胞形必須要具備嚴格的標記可遞特性,對於該幾何體內所有同維度的元素(如:點、線、面)都完全具有相同的性質,並且每一個元素皆為一個正圖形,而零維多胞形的元素僅有{F−1, F0}、負一維多胞形的元素僅有{F−1},幾何上所有零維多胞形都是正多胞形,一般地,n維正圖形被定義為有正維面[(n − 1)-表面]和正頂點圖,這兩個條件已經能充分地保證所有面、所有頂點都是相似的,但這一定義並不適用於抽象多胞形,而負一維的多胞形的僅有一種抽象多胞形。
另外,正零邊形也可以視為零維或以下的正圖形,或看做是虛無多胞形(英語:Null polytope)。
一維正圖形[编辑]

|
考克斯特記號終結點代表一個鏡射面,周圍有環的節點表示其不位於一個平面。 ditel, { }, |
在維數為一的一維空間裡存在的多胞形是由兩個端點包圍住的一個封閉一維空間,即線段。在定義上,這個一維多胞形(或稱1-多胞形)在施萊夫利符號中以: { } 表示[8][9],而在考克斯特記號中則以一個有環的節點:![]() 表示[7]。諾曼·約翰遜將之稱為ditel,並在施萊夫利符號中以{ }表示[10]。依據正圖形的定義,一個多胞形必須要具備嚴格的標記可遞特性,對於該幾何體內所有同維度的元素(如:點、線、面)都完全具有相同的性質,並且每一個元素皆為一個正圖形,而一維多胞形的旗包含{F−1, F0, F1}、其元素僅有{F−1, A, B, AB},其中,A、B為線段兩端點,由於幾何上所有零維多胞形都是正多胞形,因此所有的線段都會符合標記可遞特以及所有同維度的元素(如:點、線、面)都完全具有相同的性質,並且每一個元素皆為一個正圖形,因此在幾何上所有的一維多胞形都是正多胞形。
表示[7]。諾曼·約翰遜將之稱為ditel,並在施萊夫利符號中以{ }表示[10]。依據正圖形的定義,一個多胞形必須要具備嚴格的標記可遞特性,對於該幾何體內所有同維度的元素(如:點、線、面)都完全具有相同的性質,並且每一個元素皆為一個正圖形,而一維多胞形的旗包含{F−1, F0, F1}、其元素僅有{F−1, A, B, AB},其中,A、B為線段兩端點,由於幾何上所有零維多胞形都是正多胞形,因此所有的線段都會符合標記可遞特以及所有同維度的元素(如:點、線、面)都完全具有相同的性質,並且每一個元素皆為一個正圖形,因此在幾何上所有的一維多胞形都是正多胞形。
雖然線段做為一個多胞形是微不足道的,但它似乎是多邊形和其他更高維度圖形形成邊緣所需的一個元素[11]。在一維以及以下(包括一維、零維、負一維)空間中的多胞形都是正多胞形,包含了一維的線段、零維的點和負一維的抽象虛無多胞形都是組成多邊形和其他更高維度圖形的重要元素之一,比如一維的線段組成多邊形的邊、零維的點組成多邊形的頂點以及代表集合子集中空集合的抽象虛無多胞形都是多邊形的組成元素(子集),依據正圖形定義,若這些低為度不存在正圖形,則也不會有正多邊形和其他更高維度的正圖形。
在柱體的定義裡,線段(一維)可以被看做是點(零維)的柱體,在施萊夫利符號中以{ }×{p}表示,而在考克斯特記號中則以笛卡兒積的形式![]()
![]()
![]()
![]()
![]() 表示一個線段和多邊形[12]。
表示一個線段和多邊形[12]。
二維正多邊形[编辑]
二維凸正多邊形[编辑]
| 名稱 | 正三角形 (2-單體) |
正方形 (2-正軸形) (2-立方形) |
正五邊形 | 正六邊形 | 正七邊形 | 正八邊形 | |
|---|---|---|---|---|---|---|---|
| 施萊夫利符號 | {3} | {4} | {5} | {6} | {7} | {8} | |
| 考克斯特符号 | |||||||
| 圖像 | 
|

|

|

|

|

| |
| 名稱 | 正九邊形 | 正十邊形 | 正十一邊形 | 正十二邊形 | 正十三邊形 | 正十四邊形 | |
| 施萊夫利 | {9} | {10} | {11} | {12} | {13} | {14} | |
| 考克—迪肯 | |||||||
| 圖像 | 
|

|

|

|

|

| |
| 名稱 | 正十五邊形 | 正十六邊形 | 正十七邊形 | 正十八邊形 | 正十九邊形 | 正二十邊形 | ...正n邊形 |
| 施萊夫利 | {15} | {16} | {17} | {18} | {19} | {20} | {n} |
| 考克—迪肯 | |||||||
| 圖像 | 
|

|

|

|

|

|
- 邊數較大的正多邊形
| 名稱 | 二百五十七邊形 | 正65537邊形 | 一百萬邊形 |
|---|---|---|---|
| 可作圖? | 可作圖[13][14] | 可作圖[15][16] | 不可 |
| 施萊夫利符號 | {257}[17] | {65537}[18] | {1000000}[19] |
| 考克斯特符号 | |||
| 圖像 | 
|

|
 [20][註 10] [20][註 10]
|
退化 (圓形)[编辑]
| 名稱 | 正零邊形 | 正一邊形 | 正二邊形 |
|---|---|---|---|
| 施萊夫利符號 | {1}[21] | {2}[22] | |
| 考克斯特符号 | |||
| 圖像 | 
|

|
星形正多邊形[编辑]
| 名稱 | 五角星 | 七角星 | 八角星 | 九角星 | 十角星 | ...n角星 | ||
|---|---|---|---|---|---|---|---|---|
| 施萊夫利符號 | {5/2}[23] | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | {p/q} |
| 考克斯特符号 | ||||||||
| 圖像 | 
|

|

|

|

|

|

|
|
扭歪正多邊形[编辑]
| 扭歪六邊形 | 扭歪八邊形 | 扭歪十邊形 | ||
| D3d, [2+,6] | D4d, [2+,8] | D5d, [2+,10] | ||
|---|---|---|---|---|
| {3}#{ } | {4}#{ } | {5}#{ } | {5/2}#{ } | {5/3}#{ } |
|

|

|
|

|
三維正圖形[编辑]
三維凸正多面體[编辑]
| 名稱 | 施萊夫利符號 {p,q} |
考克斯特符号 |
圖像 (透視圖) |
圖像 (立體圖) |
圖像 (球面投影) |
面 {p} |
邊 | 頂點 {q} |
對稱群 | 對偶 |
|---|---|---|---|---|---|---|---|---|---|---|
| 正四面體 (3-單體) (三角錐) |
{3,3} | 
|

|

|
4 {3} |
6 | 4 {3} |
Td | (自身對偶) | |
| 正方體 (3-立方形) (正六面體) (四角柱) |
{4,3} | 
|

|

|
6 {4} |
12 | 8 {3} |
Oh | 正八面體 | |
| 正八面體 (3-正軸體) (正三角反棱柱) |
{3,4} | 
|

|

|
8 {3} |
12 | 6 {4} |
Oh | 立方體 | |
| 正十二面體 | {5,3} | 
|

|

|
12 {5} |
30 | 20 {3} |
Ih | 正二十面體 | |
| 正二十面體 | {3,5} | 
|

|

|
20 {3} |
30 | 12 {5} |
Ih | 正十二面體 |
退化 (球面)[编辑]
在球面幾何學中,多面形 {2,n} 和多邊形二面體 {n,2} 以及一面體 {1,1} 也可以被視為是一種正多面體(正球面鑲嵌)。
他們包括:
| 名稱 | 施萊夫利 {p,q} |
考克斯特 記號 |
圖像 (球面) |
面 {p} |
邊 | 頂點 {q} |
對稱性 | 對偶 |
|---|---|---|---|---|---|---|---|---|
| 一邊形一面體 | {1,1} | 
|
1 {1} |
0 | 1 {1} |
C1 (*1) |
自身對偶 | |
| 一邊形二面體 | {1,2} | 
|
2 {1} |
1 | 1 {2} |
C1v (*22) |
一面形 | |
| 一面形 | {2,1} | 
|
1 {2} |
1 | 2 {1} |
C1v (*22) |
一邊形二面體 | |
| 二邊形二面體 二面形 |
{2,2} | 
|
2 {2} |
2 | 2 {2} |
D2h (*222) |
自身對偶 | |
| 三面形 | {2,3} | 
|
3 {2} |
3 | 2 {3} |
D3h (*322) |
三角形二面體 | |
| 三角形二面體 | {3,2} | 
|
2 {3} |
3 | 3 {2} |
D3h (*322) |
三面形 | |
| 六面形 | {2,6} | 
|
6 {2} |
6 | 2 {6} |
D6h (*622) |
六邊形二面體 | |
| 六邊形二面體 | {6,2} | 
|
2 {6} |
6 | 6 {2} |
D6h (*622) |
六面形 |
星形正多面體[编辑]
| 名稱 | 半透明 圖像 |
立體 圖像 |
球面鑲嵌 圖像 |
星狀圖 | 施萊夫利 {p,q} 考克斯特 |
面 {p} |
邊 | 頂點 {q} 頂點圖 |
χ | 密度 | 對稱姓 | 對偶 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 小星形十二面體 | 
|

|

|

|
{5/2,5} |
12 {5/2} |
30 | 12 {5} |
−6 | 3 | Ih [5,3] (*532) |
大十二面體 |
| 大十二面體 | 
|

|

|

|
{5,5/2} |
12 {5} |
30 | 12 {5/2} |
−6 | 3 | Ih [5,3] (*532) |
小星形十二面體 |
| 大星形十二面體 | 
|

|

|

|
{5/2,3} |
12 {5/2} |
30 | 20 {3} |
2 | 7 | Ih [5,3] (*532) |
大二十面體 |
| 大二十面體 | 
|

|
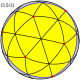
|

|
{3,5/2} |
20 {3} |
30 | 12 {5/2} |
2 | 7 | Ih [5,3] (*532) |
大星形十二面體 |
扭歪正多面體[编辑]
考克斯特在他的論文《三維和四維空間的正扭歪多面體極其類似物》[24]中列出了較多的一系列扭歪多面體,其中有四種是正圖形。

|

|

|

|
| {4, 6 | 3} | {6, 4 | 3} | {4, 8 | 3} | {8, 4 | 3} |
|---|
四維正圖形[编辑]
四維凸正多胞體[编辑]
在四維空間中存在6種凸正圖形。
| 名稱 |
施萊夫利 {p,q,r} |
考克斯特 |
胞 {p,q} |
面 {p} |
邊 {r} |
頂點 {q,r} |
對偶 {r,q,p} |
|---|---|---|---|---|---|---|---|
| 正五胞體 (四維單純形) |
{3,3,3} | 5 {3,3} |
10 {3} |
10 {3} |
5 {3,3} |
自身對偶 | |
| 正八胞體 (四維超方形) (超立方體) |
{4,3,3} | 8 {4,3} |
24 {4} |
32 {3} |
16 {3,3} |
正十六胞體 | |
| 正十六胞體 (四維正軸體) |
{3,3,4} | 16 {3,3} |
32 {3} |
24 {4} |
8 {3,4} |
超立方體 | |
| 正二十四胞體 | {3,4,3} | 24 {3,4} |
96 {3} |
96 {3} |
24 {4,3} |
自身對偶 | |
| 正一百二十胞體 (四維類五邊形體) |
{5,3,3} | 120 {5,3} |
720 {5} |
1200 {3} |
600 {3,3} |
正六百胞體 | |
| 正六百胞體 (四維類二十面體體 |
{3,3,5} | 600 {3,3} |
1200 {3} |
720 {5} |
120 {3,5} |
正一百二十胞體 |
| 正五胞體 | 超立方體 | 正十六胞體 | 正二十四胞體 | 正一百二十胞體 | 正六百胞體 |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
| 線架圖 (皮特里多邊形) 歪斜正投影圖 | |||||

|

|

|

|

|

|
| 不透明正投影圖 | |||||
 被正四面體包覆 (以頂點與胞為中心) |
 被立方體包覆 (以胞為中心) |
 被立方體包覆 (以胞為中心) |
 被截半立方體包覆 (以胞為中心) |
 被倒角十二面體包覆 (以胞為中心) |
 被五角化截半二十面體包覆 (以頂點為中心) |
| 施萊蓋爾線框 (透視投影) | |||||
 (以胞為中心) |
 (以胞為中心) |
 (以胞為中心) |
 (以胞為中心) |
 (以胞為中心) |
 (以頂點為中心) |
| 球極平面投影線框 (超球面堆砌) | |||||

|

|

|

|

|

|
退化 (超球面)[编辑]
| 施萊夫利 {2,p,q} |
考克斯特符号 |
胞 {2,p}π/q |
面 {2}π/p,π/q |
邊 | 頂點 | 頂點圖 {p,q} |
對稱性 | 對偶多胞形 |
|---|---|---|---|---|---|---|---|---|
| {2,3,3} | 4 {2,3}π/3 
|
6 {2}π/3,π/3 |
4 | 2 | {3,3}
|
[2,3,3] | {3,3,2} | |
| {2,4,3} | 6 {2,4}π/3 
|
12 {2}π/4,π/3 |
8 | 2 | {4,3}
|
[2,4,3] | {3,4,2} | |
| {2,3,4} | 8 {2,3}π/4 
|
12 {2}π/3,π/4 |
6 | 2 | {3,4}
|
[2,4,3] | {4,3,2} | |
| {2,5,3} | 12 {2,5}π/3 
|
30 {2}π/5,π/3 |
20 | 2 | {5,3}
|
[2,5,3] | {3,5,2} | |
| {2,3,5} | 20 {2,3}π/5 
|
30 {2}π/3,π/5 |
12 | 2 | {3,5}
|
[2,5,3] | {5,3,2} |
扭歪多胞體[编辑]
四維的扭歪多胞體是一些位於五維或以上的扭歪圖形。
五維正圖形[编辑]
五維凸正多胞體[编辑]
| 名稱 | 施萊夫利 {p,q,r,s} 考克斯特 |
維面 {p,q,r} |
胞 {p,q} |
面 {p} |
邊 | 頂點 | 面圖 {s} |
邊圖 {r,s} |
頂點圖 {q,r,s} |
|---|---|---|---|---|---|---|---|---|---|
| 五維正六胞體 | {3,3,3,3} |
6 {3,3,3} |
15 {3,3} |
20 {3} |
15 | 6 | {3} | {3,3} | {3,3,3} |
| 五維超正方體 | {4,3,3,3} |
10 {4,3,3} |
40 {4,3} |
80 {4} |
80 | 32 | {3} | {3,3} | {3,3,3} |
| 五維正三十二胞體 | {3,3,3,4} |
32 {3,3,3} |
80 {3,3} |
80 {3} |
40 | 10 | {4} | {3,4} | {3,3,4} |
 五維正六胞體 |
 五維超正方體 |
 五維正三十二胞體 |
六維正圖形[编辑]
六維凸正多胞體[编辑]
| 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 胞 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|
| 六維正七胞體 | {3,3,3,3,3} | 7 | 21 | 35 | 35 | 21 | 7 | 0 |
| 六維超立方體 | {4,3,3,3,3} | 64 | 192 | 240 | 160 | 60 | 12 | 0 |
| 六維正六十四胞體 | {3,3,3,3,4} | 12 | 60 | 160 | 240 | 192 | 64 | 0 |
 六維正七胞體 |
 六維超立方體 |
 六維正六十四胞體 |
七維正圖形[编辑]
七維凸正多胞體[编辑]
| 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 胞 | 維峰 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|---|
| 七維正八胞體 | {3,3,3,3,3,3} | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 2 |
| 七維超立方體 | {4,3,3,3,3,3} | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 2 |
| 七維正一百二十八胞體 | {3,3,3,3,3,4} | 14 | 84 | 280 | 560 | 672 | 448 | 128 | 2 |
 七維正八胞體 |
 七維超立方體 |
 七維正一百二十八胞體 |
七維以上正圖形[编辑]
n維凸正多胞體[编辑]
從五維開始,凸正多胞體都只有三種[25]。
| 名稱 | 施萊夫利 符號 {p1,...,pn−1} |
考克斯特 記號 |
k維胞 / 面 | 維面 | 頂點圖 | 對偶 |
|---|---|---|---|---|---|---|
| n維單體 | {3n−1} | {3n−2} | {3n−2} | 自身對偶 | ||
| n維超立方體 | {4,3n−2} | {4,3n−3} | {3n−2} | n維正軸體 | ||
| n維正軸體 | {3n−2,4} | {3n−2} | {3n−3,4} | n維超立方體 |
八維[编辑]
| 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 胞 | 4維胞 | 維峰 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|---|---|
| 八維單體 | {3,3,3,3,3,3,3} | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 0 |
| 八維超立方體 | {4,3,3,3,3,3,3} | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 0 |
| 八維正軸體 | {3,3,3,3,3,3,4} | 16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | 0 |
 八維單體 |
 八維超立方體 |
 八維正軸體 |
九維[编辑]
| 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 胞 | 4維胞 | 5維胞 | 維峰 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 九維單體 | {38} | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 2 |
| 九維超立方體 | {4,37} | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 2 |
| 九維正軸體 | {37,4} | 18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | 2 |
 九維單體 |
 九維超立方體 |
 九維正軸體 |
十維[编辑]
| 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 胞 | 4維胞 | 5維胞 | 6維胞 | 維峰 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 十維單體 | {39} | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 0 |
| 十維超立方體 | {4,38} | 1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | 0 |
| 十維正軸體 | {38,4} | 20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | 0 |
 十維單體 |
 十維超立方體 |
 十維正軸體 |
十一維[编辑]
| 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 胞 | 4維胞 | 5維胞 | 6維胞 | 7維胞 | 維峰 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 十一維單體 | {310} | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 2 |
| 十一維超立方體 | {4,39} | 2048 | 11264 | 28160 | 42240 | 42240 | 29568 | 14784 | 5280 | 1320 | 220 | 22 | 2 |
| 十一維正軸體 | {39,4} | 22 | 220 | 1320 | 5280 | 14784 | 29568 | 42240 | 42240 | 28160 | 11264 | 2048 | 2 |
 十一維單體 |
 十一維超立方體 |
 十一維正軸體 |
十二維[编辑]
| 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 胞 | 4維胞 | 5維胞 | 6維胞 | 7維胞 | 8維胞 | 維峰 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 十二維單體 | {311} | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 | 78 | 13 | 0 |
| 十二維超立方體 | {4,310} | 4096 | 24576 | 67584 | 112640 | 126720 | 101376 | 59136 | 25344 | 7920 | 1760 | 264 | 24 | 0 |
| 十二維正軸體 | {310,4} | 24 | 264 | 1760 | 7920 | 25344 | 59136 | 101376 | 126720 | 112640 | 67584 | 24576 | 4096 | 0 |
 十二維單體 |
 十二正軸體 |
更高維度[编辑]
| 種類 | 維度 | 名稱 | 施萊夫利 | 頂點 | 邊 | 面 | 維峰 | 維脊 | 維面 | χ |
|---|---|---|---|---|---|---|---|---|---|---|
| 单纯形 | 13 | 十三維單體 | {312} | 14 | 91 | 364 | 364 | 91 | 14 | 2 |
| 14 | 十四維單體 | {313} | 15 | 105 | 455 | 455 | 105 | 15 | 0 | |
| 15 | 十五維單體 | {314} | 16 | 120 | 560 | 560 | 120 | 16 | 2 | |
| 16 | 十六維單體 | {315} | 17 | 136 | 680 | 680 | 136 | 17 | 0 | |
| 17 | 十七維單體 | {316} | 18 | 153 | 816 | 816 | 153 | 18 | 2 | |
| 18 | 十八維單體 | {317} | 19 | 171 | 969 | 969 | 171 | 19 | 0 | |
| 19 | 十九維單體 | {318} | 20 | 190 | 1140 | 1140 | 190 | 20 | 2 | |
| 20 | 二十維單體 | {319} | 21 | 210 | 1330 | 1330 | 210 | 21 | 0 | |
| 超方形 | 13 | 十三維超立方體 | {4,311} | 8192 | 53248 | 159744 | 2288 | 312 | 26 | 2 |
| 14 | 十四維超立方體 | {4,312} | 16384 | 114688 | 372736 | 2912 | 364 | 28 | 0 | |
| 15 | 十五維超立方體 | {4,313} | 32768 | 245760 | 860160 | 3640 | 420 | 30 | 2 | |
| 16 | 十六維超立方體 | {4,314} | 65536 | 524288 | 1966080 | 4480 | 480 | 32 | 0 | |
| 17 | 十七維超立方體 | {4,315} | 131072 | 1114112 | 4456448 | 5440 | 544 | 34 | 2 | |
| 18 | 十八維超立方體 | {4,316} | 262144 | 2359296 | 10027008 | 6528 | 612 | 36 | 0 | |
| 19 | 十九維超立方體 | {4,317} | 524288 | 4980736 | 22413312 | 7752 | 684 | 38 | 2 | |
| 20 | 二十維超立方體 | {4,318} | 1048576 | 10485760 | 49807360 | 9120 | 760 | 40 | 0 | |
| 正轴形 | 13 | 十三維正軸體 | {311,4} | 26 | 312 | 2288 | 159744 | 53248 | 8192 | 2 |
| 14 | 十四維正軸體 | {312,4} | 28 | 364 | 2912 | 372736 | 114688 | 16384 | 0 | |
| 15 | 十五維正軸體 | {313,4} | 30 | 420 | 3640 | 860160 | 245760 | 32768 | 2 | |
| 16 | 十六維正軸體 | {314,4} | 32 | 480 | 4480 | 1966080 | 524288 | 65536 | 0 | |
| 17 | 十七維正軸體 | {315,4} | 34 | 544 | 5440 | 4456448 | 1114112 | 131072 | 2 | |
| 18 | 十八維正軸體 | {316,4} | 36 | 612 | 6528 | 10027008 | 2359296 | 262144 | 0 | |
| 19 | 十九維正軸體 | {317,4} | 38 | 684 | 7752 | 22413312 | 4980736 | 524288 | 2 | |
| 20 | 二十維正軸體 | {318,4} | 40 | 760 | 9120 | 49807360 | 10485760 | 1048576 | 0 |
n維正非凸多胞形[编辑]
從五維開始就都不存在任何非凸多胞形。
正無窮多胞形[编辑]
一維[编辑]
密鋪[编辑]
對應的歐幾里得密鋪只有一種,密鋪於一維歐幾里得空間,即直線,即正無限邊形。其施萊夫利符號以{∞}表示、考克斯特符号以![]()
![]()
![]() 表示。
表示。
該鑲嵌是由一維正圖形「線段」(即二維二邊形)完成一維歐幾里得空間的密鋪。
雙曲密鋪[编辑]
對應的雙曲密鋪只有一種,即由一維正圖形「線段」完成一維羅氏空間(即二維雙曲線)的密鋪,類似於無限邊形,稱為超無限邊形,但又因為它是發散的,因此又稱為偽多邊形。在施萊夫利符號以{iπ/λ}表示、考克斯特符号以![]()
![]()
![]() 表示。
表示。
二維[编辑]
平面正鑲嵌圖[编辑]
| 名稱 | 正方形鑲嵌 | 正三角形鑲嵌 | 正六邊形鑲嵌 |
|---|---|---|---|
| 對稱群 | p4m, [4,4], (*442) | p6m, [6,3], (*632) | |
| 施萊夫利 {p,q} | {4,4} | {3,6} | {6,3} |
| 考克斯特記號 | |||
| 圖像 | 
|

|

|
雙曲凸正鑲嵌圖[编辑]
| 雙曲正鑲嵌圖 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 球面 (退化/柏拉圖)/平面/雙曲面 (龐加萊圓盤: 緊湊/仿緊湊/非緊湊) 鑲嵌圖與其施萊夫利符號 | |||||||||||
| p \ q | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ∞ | ... | iπ/λ |
| 2 |  {2,2} |
 {2,3} |
 {2,4} |
 {2,5} |
 {2,6} |
 {2,7} |
 {2,8} |
{2,∞} |
 {2,iπ/λ} | ||
| 3 |  {3,2} |
 (正四面體) {3,3} |
 (正八面體) {3,4} |
 (正二十面體) {3,5} |
 (三角鑲嵌) {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} |
 {3,iπ/λ} | ||
| 4 |  {4,2} |
 (立方體) {4,3} |
 (方形鑲嵌) {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8} |
 {4,∞} |
 {4,iπ/λ} | ||
| 5 |  {5,2} |
 (十二面體) {5,3} |
 {5,4} |
 {5,5} |
 {5,6} |
 {5,7} |
 {5,8} |
 {5,∞} |
 {5,iπ/λ} | ||
| 6 |  {6,2} |
 (六角鑲嵌) {6,3} |
 {6,4} |
 {6,5} |
 {6,6} |
 {6,7} |
 {6,8} |
 {6,∞} |
 {6,iπ/λ} | ||
| 7 | {7,2} |
 {7,3} |
 {7,4} |
 {7,5} |
 {7,6} |
 {7,7} |
 {7,8} |
 {7,∞} |
{7,iπ/λ} | ||
| 8 | {8,2} |
 {8,3} |
 {8,4} |
 {8,5} |
 {8,6} |
 {8,7} |
 {8,8} |
 {8,∞} |
{8,iπ/λ} | ||
| ⋮ | |||||||||||
| ∞ |  {∞,2} |
 {∞,3} |
 {∞,4} |
 {∞,5} |
 {∞,6} |
 {∞,7} |
 {∞,8} |
 {∞,∞} |
 {∞,iπ/λ} | ||
| ⋮ | |||||||||||
| iπ/λ |  {iπ/λ,2} |
 {iπ/λ,3} |
 {iπ/λ,4} |
 {iπ/λ,5} |
 {iπ/λ,6} |
{iπ/λ,7} |
{iπ/λ,8} |
 {iπ/λ,∞} |
 {iπ/λ,iπ/λ} | ||
雙曲星形正鑲嵌圖[编辑]
| 名稱 | 施萊夫利符號 | 考克斯特符號 | 圖像 | 面的種類 {p} |
頂點圖 {q} |
密度 | 對稱 | 對偶 |
|---|---|---|---|---|---|---|---|---|
| 七階七角星鑲嵌 | {7/2,7} | 
|
{7/2} |
{7} |
3 | *732 [7,3] |
二分之七階七邊形鑲嵌 | |
| 二分之七階七邊形鑲嵌 | {7,7/2} | 
|
{7} |
{7/2} |
3 | *732 [7,3] |
七階七角星鑲嵌 | |
| 九階九角星鑲嵌 | {9/2,9} | 
|
{9/2} |
{9} |
3 | *932 [9,3] |
二分之九階九邊形鑲嵌 | |
| 二分之九階九邊形鑲嵌 | {9,9/2} | 
|
{9} |
{9/2} |
3 | *932 [9,3] |
九階九角星鑲嵌 | |
| 十一階十一角星鑲嵌 | {11/2,11} | 
|
{11/2} |
{11} |
3 | *11.3.2 [11,3] |
二分之十一階十一邊形鑲嵌 | |
| 二分之十一階十一邊形鑲嵌 | {11,11/2} | 
|
{11} |
{11/2} |
3 | *11.3.2 [11,3] |
十一階十一角星鑲嵌 | |
| p階p角星鑲嵌 | {p/2,p} | {p/2} | {p} | 3 | *p32 [p,3] |
二分之p階p邊形鑲嵌 | ||
| 二分之p階p邊形鑲嵌 | {p,p/2} | {p} | {p/2} | 3 | *p32 [p,3] |
p階p角星鑲嵌 | ||
| ... | ||||||||
| 無限階無限角星鑲嵌[註 11] | {∞/2,∞} | 
|
{∞/2} | {∞} | 3 | *∞.3.2 [∞,3] |
二分之無限階無限邊形鑲嵌[註 11] | |
| 二分之無限階無限邊形鑲嵌[註 11] | {∞,∞/2} | 
|
{∞} | {∞/2} | 3 | *∞.3.2 [∞,3] |
無限階無限角星鑲嵌[註 11] | |
三維[编辑]

三維空間中只有一種正堆砌體,即立方體堆砌{4, 3, 4}:[7]
| 名稱 | 施萊夫利 {p,q,r} |
考克斯特 |
胞 {p,q} |
面 {p} |
邊圖 {r} |
頂點圖 {q,r} |
χ | 對偶 |
|---|---|---|---|---|---|---|---|---|
| 立方體堆砌 | {4,3,4} | {4,3} | {4} | {4} | {3,4} | 0 | 自身對偶 |
四維[编辑]
| 名稱 | 施萊夫利 {p,q,r,s} |
維面 {p,q,r} |
胞 {p,q} |
面 {p} |
面圖 {s} |
邊圖 {r,s} |
頂點圖 {q,r,s} |
對偶 |
|---|---|---|---|---|---|---|---|---|
| 超立方體堆砌 | {4,3,3,4} | {4,3,3} | {4,3} | {4} | {4} | {3,4} | {3,3,4} | 自身對偶 |
| 正十六胞體堆砌 | {3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,4,3,3} |
| 正二十四胞體堆砌 | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {4,3,3} | {3,3,4,3} |
 超立方體堆砌 |
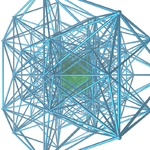 正十六胞體堆砌 |
 正二十四胞體堆砌 |
五維[编辑]
五維空間的正堆砌僅有五維超立方體堆砌{4,3,3,3,4}[26]
| 名稱 | 施萊夫利 {p,q,r,s,t} |
考克斯特 |
維面 {p,q,r,s} |
維脊 {p,q,r} |
胞 {p,q} |
面 {p} |
邊圖 {t} |
頂點圖 {s,t} |
對偶 |
|---|---|---|---|---|---|---|---|---|---|
| 五維超立方體堆砌 | {4,3,3,3,4} | {4,3,3,3} | {4,3,3} | {4,3} | {4} | {4} | {3,4} | 自身對偶 |
六維以上[编辑]
| δn | 維度 | 名稱 | 施萊夫利 | 考克斯特 | |||
|---|---|---|---|---|---|---|---|
| 原位 {∞}n (2m色, m<n) |
正 {4,3n-1,4} (1色、n色) |
網格 {4,3n-4,31,1} (2色) | |||||
| δ6 | 五維(退化六維) | 五維超立方體堆砌 | {∞}5 {4,33,4} {4,32,31,1} |
||||
| δ7 | 六維(退化七維) | 六維超立方體堆砌 | {∞}6 {4,34,4} {4,33,31,1} |
||||
| δ8 | 七維(退化八維) | 七維超立方體堆砌 | {∞}7 {4,35,4} {4,34,31,1} |
||||
| δ9 | 八維(退化九維) | 八維超立方體堆砌 | {∞}8 {4,36,4} {4,35,31,1} |
||||
| δn | n-1維(退化n維) | n-1維超立方體堆砌 | {∞}n {4,3n-3,4} {4,3n-4,31,1} |
... | |||
雙曲[编辑]
六維或以上的維度皆不存在緊空間與仿緊空間的雙曲堆砌。不過,任何的{p,q,r,s,...}形式(其中p,q,r,s,...是大於二的自然數或無限大)以上並不包括n維空間的非緊鑲嵌。
非緊鑲嵌[编辑]
| 維 | 總數 | 群 | ||||
|---|---|---|---|---|---|---|
| 三維(退化四維) | ∞ | [3,3,7] ... [∞,∞,∞]: [4,3[3]] ... [∞,∞[3]]: | ||||
| 四維(退化五維) | 186 | ...[3[3,3,3]]: |
||||
| 五維(退化六維) | 66 | |||||
| 六維(退化七維) | 36 | [31,1,1,1,1,1]: | ||||
| 七維(退化八維) | 13 |
[3,3,3[6]]: |
[4,3,3,33,1]: |
[4,3,3,32,2]: | ||
| 八維(退化九維) | 10 |
[3,3[3+4],3]: |
[32,1,32,32,1]: |
[33,1,33,4]: [33,1,3,3,31,1]: |
[33,3,2]: [32,2,4]: | |
| 九維(退化十維) | 8 | [3,3[8],3]: [3,3[3+5],3]: |
[32,1,33,32,1]: |
[35,3,1]: [33,1,34,4]: |
[34,4,1]: | |
| 十維(退化十一維) | 4 | [32,1,34,32,1]: |
[32,1,36,4]: [32,1,35,31,1]: |
[37,2,1]: | ||
複合正圖形[编辑]
二維複合正多邊形[编辑]
 2{2} |
3{2} |
 4{2} |
5{2} |
 6{2} |
7{2} |
 8{2} |
9{2} |
 10{2} |
 11{2} |
 12{2} |
 13{2} |
 14{2} |
 15{2} | |
2{3} |
 3{3} |
 4{3} |
 5{3} |
6{3} |
 7{3} |
 8{3} |
 9{3} |
 10{3} |
 2{4} |
 3{4} |
 4{4} |
 5{4} |
 6{4} |
 7{4} |
2{5} |
 3{5} |
 4{5} |
 5{5} |
 6{5} |
2{5/2} |
 3{5/2} |
 4{5/2} |
 5{5/2} |
 6{5/2} |
 2{6} |
3{6} |
 4{6} |
 5{6} | |
2{7} |
 3{7} |
 4{7} |
2{7/2} |
 3{7/2} |
 4{7/2} |
2{7/3} |
 3{7/3} |
 4{7/3} |
 2{8} |
 3{8} |
 2{8/3} |
 3{8/3} | ||
2{9} |
 3{9} |
2{9/2} |
 3{9/2} |
2{9/4} |
 3{9/4} |
 2{10} |
 3{10} |
 2{10/3} |
 3{10/3} | |||||
 2{11} |
 2{11/2} |
 2{11/3} |
 2{11/4} |
 2{11/5} |
 2{12} |
 2{12/5} |
 2{13} |
 2{13/2} |
 2{13/3} |
 2{13/4} |
 2{13/5} |
 2{13/6} | ||
 2{14} |
 2{14/3} |
 2{14/5} |
 2{15} |
 2{15/2} |
 2{15/4} |
 2{15/7} |
抽象正圖形[编辑]
多面體 
內側菱形三十面體
十二合十二面體
內側三角星化二十面體
雙三斜十二面體
凹五角錐十二面體頂點圖 {5}, {5/2} 

(5.5/2)2 
{5}, {5/2} 

(5.5/3)3 

面 30個菱形 
12個五邊形
12個五角星

20個六邊形 
12個五邊形
12個五角星

20個六邊形 
鑲嵌 
{4, 5}
{5, 4}
{6, 5}
{5, 6}
{6, 6}χ −6 −6 −16 −16 −20
參見[编辑]
註釋[编辑]
參考文獻[编辑]
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V, pp. 212–213) [1] (页面存档备份,存于互联网档案馆) PDF
- D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
- ^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 George Maxwell, Sphere Packings and Hyperbolic Reflection Groups Archive.is的存檔,存档日期2013-06-30, JOURNAL OF ALGEBRA 79,78-97 (1982)
- ^ Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, http://arxiv.org/abs/1310.8608 (页面存档备份,存于互联网档案馆)
- ^ Wolcott, Luke; McTernan, Elizabeth. Imagining Negative-Dimensional Space (PDF). Bosch, Robert; McKenna, Douglas; Sarhangi, Reza (编). Proceedings of Bridges 2012: Mathematics, Music, Art, Architecture, Culture. Phoenix, Arizona, USA: Tessellations Publishing: 637–642. 2012 [10 July 2015]. ISBN 978-1-938664-00-7. ISSN 1099-6702. (原始内容 (PDF)存档于2015-06-26).
- ^ 4.0 4.1 McMullen, Peter; Schulte, Egon, Abstract Regular Polytopes 1st, Cambridge University Press, December 2002, ISBN 0-521-81496-0
- ^ zero dimensional. planetmath.org. [2015-06-06]. (原始内容存档于2015-06-24).
- ^ Hazewinkel, Michiel. Encyclopaedia of Mathematics, Volume 3. Kluwer Academic Publishers. 1989: 190 [2016-07-15]. (原始内容存档于2019-09-05).
- ^ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- ^ Coxeter Regular Polytopes(1973)[7], p. 129
- ^ Abstract Regular Polytopes(2002)[4], p. 30
- ^ Johnson (2012), p. 86
- ^ Coxeter Regular Polytopes(1973)[7], p. 120
- ^ Coxeter Regular Polytopes(1973)[7], p. 124
- ^ Richelot, Friedrich Julius. De resolutione algebraica aequationis X257 = 1, sive de divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata. Journal für die reine und angewandte Mathematik. 1832, 9: pp. 1–26, 146–161, 209–230, 337–358 (拉丁语).
- ^ Coxeter, H. S. M. Introduction to Geometry 2nd ed. New York: Wiley. February 1989. ISBN 978-0-471-50458-0.
- ^ Hermes, Johann Gustav. Ueber die Teilung des Kreises in 65537 gleiche Teile. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (Göttingen). 1894, 3: pp. 170–186 (德语).
- ^ Hermes, Johann Gustav. Ueber die Teilung des Kreises in 65537 gleiche Teile. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (Göttingen). 1894, 3: pp. 170–186 [2016-08-10]. (原始内容存档于2017-01-11) (德语).
- ^ Weisstein, Eric W. (编). 257-gon. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). 65537-gon. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Darling, David J., The universal book of mathematics: from Abracadabra to Zeno's paradoxes, John Wiley & Sons, 2004. Page 249. ISBN 0-471-27047-4.
- ^ Russell, Bertrand, History of Western Philosophy (页面存档备份,存于互联网档案馆), reprint edition, Routledge, 2004, p. 202, ISBN 0-415-32505-6.
- ^ Coxeter, Introduction to geometry, 1969, Second edition, sec 21.3 Regular maps, p. 386-388
- ^ Weisstein, Eric W. (编). Digon. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Pentagram. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.
- ^ Coxeter Regular Polytopes(1973)[7], Table I: Regular polytopes, (iii) The three regular polytopes in n dimensions (n>=5), pp. 294–295.
- ^ Coxeter Regular Polytopes(1973)[7], p. 296, Table II: Regular honeycombs
外部連結[编辑]
- The Platonic Solids (页面存档备份,存于互联网档案馆)
- Kepler-Poinsot Polyhedra (页面存档备份,存于互联网档案馆)
- Regular 4d Polytope Foldouts
- Multidimensional Glossary (Look up Hexacosichoron and Hecatonicosachoron)
- Polytope Viewer (页面存档备份,存于互联网档案馆)
- Polytopes and optimal packing of p points in n dimensional spheres
- An atlas of small regular polytopes (页面存档备份,存于互联网档案馆)
| ||||||||||||||||||||||

























































