泊肃叶定律

泊肃叶定律(英語:Poiseuille's law)[1]也稱為泊谡叶方程、帕醉定律、哈根-泊肃叶定律(Hagen-Poiseuille's law)、哈根-帕醉方程(Hagen-Poiseuille's equation),是描述流體流经细管(如血管和导尿管等)所產生的壓力損失,壓力損失和體積流率、動黏度和管長的乘積成正比,和管径的四次方成反比例。此定律適用於不可壓縮、不具有加速度、層流穩定且長於管徑的牛頓流體。泊肃叶定律是让·泊肃叶于1838年和戈特希尔夫·哈根于1838和1839年分别实验独立发现的,並于1840年和1846年发表。
泊肃叶定律的应用前提有七:
- 假设液体是不可压缩流體;
- 假设液体是牛顿流体,即它的粘滞系数不随流速而改变;
- 假设液体的流动是层流,而不是湍流,即管的直径不能太大。
- Fully Develop,液體在管內速度場為全展開
- Steady state, 穩定流態
- Circular pipe, 流體在圓形管內流動
- 忽略End effect 終端效應
公式[编辑]
標準流體力學的表示法[编辑]
或
其中
物理表示法[编辑]
其中的單位如下,單位則是以相容的單位為主(例如國際單位制)
- 是體積流率(標準流體力學表示法中的)
- 是流過的液體體積函數,參數為時間
- 是沿著細管的平均流體速度
- 是沿著流體流動方向的距離
- 是細管的內半徑
- 是細管兩端的壓力損失
- 是動黏度,SI制單位為Pa·s
- 是細管的長度
此公式在細管进口段的誤差較大[4]:3。
此公式不適用在低黏度、短管、寬管或流體流速高的條件下。低黏度、高流速或寬管的條件會產生紊流,導致該流體的壓力差較此定律所預測的值為大。因此需要用到像是达西-韦史巴赫方程之類較複雜的模型。若管子太短,泊肃叶定律會計算出不實際的高體積流率。此公式所計算出的流體流率,被限制在較寬鬆條件的伯努利定律結果之內:
推導[编辑]
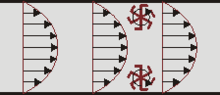
泊肃叶定律可以由纳维-斯托克斯方程推導而來,但若已知管子中的層流,其速度分布呈拋物線[5]:
在相同直徑處的速度也會相同,因此將相同直徑處的流體視為一薄層,流過薄層流體的體積流量等於速度乘以薄層的截面積:
再將上述的量對半徑r積分,即可得到總流量。
和达西-韦史巴赫方程的關係[编辑]
泊肃叶定律不只是有關壓力損失和流速的公式,也和管子中的層流,其速度分布呈拋物線有關[5]。不過只要推定紊流下的有效紊流黏度,也可以將上述壓力損失的公式延伸到紊流的情形,即使紊流速度分布已不呈拋物線也沒關係。在層流和紊流的情形下,壓力損失都和管壁的應力有關,由管壁應力可以定義所謂的摩擦因數。在水力学的領域中,管壁應力可以用达西-韦史巴赫方程求得,其中摩擦因數表示為和雷諾數和其他物理量的函數。若在層流的情形下:
其中
- 為摩擦因數
- 為雷諾數
- 為流體密度
- 為平均流體速度,在層流的情形下會是最大流體速度的一半
上述式子用平均流體速度來定義雷諾數,因此其實用性提高。因為在紊流其最大流體速度很難計算。此公式可以近似达西摩擦因数。是圓型管子下流速很低的層流下的摩擦因數。韦德曼(Wiedman)曾在1856年獨立的進行和此定律型式稍微不同的定律的推導,諾伊曼和哈根巴赫(E. Hagenbach)也曾在1858年推導過型式不完全一様的定律。哈根巴赫是第一個稱此定律為泊肃叶定律的人。
泊肃叶定律在生理学中的血液流变学和血液動力学中非常的重要[6]。
1891年時L. R. Wilberforce以哈根巴赫的研究為基礎,將泊肃叶定律擴展到紊流的領域中。
可壓縮流體下的泊肃叶定律[编辑]
若管中的是可壓縮流體,其體積流率及線速度會延著管子變化。流體一般會以出口處的壓力來表示,當流體壓縮或是膨脹時,流體會作功,溫度可能上昇或是下降,因此流體流率和流體與外界的熱交換有關。若是在等温过程下的理想氣體,也就是氣體溫度和外界平衡時,而且管子兩端的壓力差很小時,其出口處的體積流率可以表示如下式:
其中
當流體的馬赫數小於0.3時,可以用上式近似實際的體積流率。
上式可以視為是增加一修正係數的泊肃叶定律,修正係數是考慮平均壓力相對於出口壓力的比例。
和電路的類比[编辑]
電子一開始也是當作一種流體來了解,水力類比的概念在了解電子電路上仍十分有用。這種類比方式也用來研究流體機械網路的頻率響應,其中流體機械網路會以液压回路來表示。
泊肃叶定律對應電路中的歐姆定律(),其中壓力差對應電壓,而體積流率對應電流,則以下的物理量對應電阻
一個管子的有效阻力和半徑倒數的四次方成正比,因此管子的半俓減半會使管子的阻力變為原來的16倍。
歐姆定律和泊肃叶定律都是對於輸運現象的描述。
相關條目[编辑]
参考文献[编辑]
- ^ Sutera, S P; Skalak, R. The History of Poiseuille's Law. Annual Review of Fluid Mechanics. 1993-01, 25 (1): 1–20. ISSN 0066-4189. doi:10.1146/annurev.fl.25.010193.000245.
- ^ Kirby, Brian. Preface. Micro- and Nanoscale Fluid Mechanics. Cambridge: Cambridge University Press. : xv–xvi. ISBN 978-0-511-76072-3.
- ^ Bruus, Henrik. Theoretical microfluidics. Oxford Univ. Press. 2011. ISBN 978-0-19-923509-4. OCLC 753178868.
- ^ Vogel, Steven, author. Life in Moving Fluids : The Physical Biology of Flow - Revised and Expanded Second Edition. ISBN 0-691-21297-X. OCLC 1158109140.
- ^ 5.0 5.1 層流與擾流. [2014-01-07]. (原始内容存档于2014-01-07).
- ^ Determinants of Resistance to Flow (Poiseuille's Equation). CV Physiology. [2020-09-29]. (原始内容存档于2021-01-18).































