闵可夫斯基图
閔可夫斯基圖(Minkowski diagram)是一種時空圖(spacetime diagram),用以表示閔可夫斯基時空的事件的坐標。它是一種理解狹義相對論現象的工具。
在四維的坐標系,以時間乘以光速(ct)為其中一軸,稱之為時間軸;其他的x軸、y軸、z軸,稱之為空間軸。在這四維時空上的每一點,都代表一個事件E。對應特定的慣性參考系,E發生的時間和地點(ct,x,y,z)。
每個質點在時空的活動都可以在時空圖上以連續的曲線表示,稱為世界線。
例如,在直角坐標系上,若質點均速運動,,它的世界線便是一條穿過原點、斜率為的直線(斜率是关于时间轴ct轴的,而非x轴)。若質點是簡諧運動, ,它的世界線便會一條沿時間軸變化的正弦曲線。
(為了方便在平面上表示,下面的閔可夫斯基圖多數只有時間軸和一條空間軸x軸。)
坐標轉換[编辑]

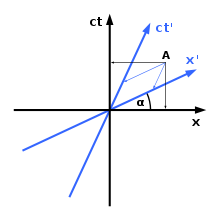
對應慣性參考系O,它在一閔可夫斯基圖為直角坐標系。若另一個慣性參考系O'對應O以均速沿x方向行進,則有慣性坐標系O',x'軸跟x軸的夾角等於軸和軸的夾角,夾角。
若事件E在直角坐標系O的坐標為(ct, x),量度E在O'的坐標時,長度需除以 。這個長度的變化是因為兩個坐標系原時的不同。
光錐[编辑]


若有一道光經過(0,0,0,0),它所有可能的世界線是兩個圓錐面,圓錐的頂角是90°,一個在(未來),另一個在(過去),稱為光錐。圓錐面將平面分成五部分
- 未來光錐內的點(表示的事件),與原點是類空的;
- 過去光錐內的點,與原點是類空的;
- 光錐外的點(有兩邊),與原點是類時的;
- 在光錐上的點,是類光的。
空間收縮[编辑]

考察一條原長為L的木棒,在閔可夫斯基圖畫出棒端和棒末的軌跡。兩點的軌跡是平行直線。
從圖中可見,若觀察者A與棒之間有相對速度,A量度棒的長度,從一個與棒相對速度為0的觀察者的慣性系(即棒的體慣性系)看來,對方量度棒端和棒末的時間不同。經過計算(要記得在不同慣性系在圖中的單位長度不同),便可知道棒的長度,在體慣性系量度得的長度是最大,其他慣性系的觀察者都會量得L' < L,即有空間收縮。
時空圖的其他應用可參見雙生子佯謬。
與其他坐標轉換的比較[编辑]


另见[编辑]
| |||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












