一筆畫問題
一筆畫問題(Eulerian graph)是圖論中一個著名的問題。一筆畫問題起源於柯尼斯堡七橋問題。數學家歐拉在他1736年發表的論文《柯尼斯堡的七橋》中不僅解決了七橋問題,也提出了一筆畫定理,順帶解決了一筆畫問題[1]。一般認為,歐拉的研究是圖論的開端。
能夠在不重複折返的前提下一筆畫寫出或一次走完該路徑的條件,是文字、圖形、路徑的奇頂點的數目正好是0個或2個時,而如果奇頂點的數目兩個時,必須正好為起點或終點,奇頂點是指該點延展出奇數數目的方向,例如T字路口延展出三條道路方向,而線段的端點也是只有一個方向的奇頂點
問題的提出[編輯]
一筆畫問題是柯尼斯堡問題經抽象化後的推廣,是圖遍歷問題的一種。在柯尼斯堡問題中,如果將橋所連接的地區視為點,將每座橋視為一條邊,那麼問題將變成:對於一個有着四個頂點和七條邊的連通圖 ,能否找到一個恰好包含了所有的邊,並且沒有重複的路徑。歐拉將這個問題推廣為:對於一個給定的圖,怎樣判斷是否存在着一個恰好包含了所有的邊,並且沒有重複的路徑?這就是一筆畫問題。用圖論的術語來說,就是判斷這個圖是否是一個能夠遍歷完所有的邊而沒有重複。這樣的圖現稱為歐拉圖。這時遍歷的路徑稱作歐拉路徑(一個環或者一條鏈),如果路徑閉合(一個圈),則稱為歐拉迴路[1]。
一筆畫問題的推廣是多筆畫問題,即對於不能一筆畫的圖,探討最少能用多少筆來畫成。
一筆畫定理[編輯]
對於一筆畫問題,有兩個判斷的準則,它們都由歐拉提出並證明[1]。
定理一[編輯]
連通的無向圖 有歐拉路徑的充要條件是:中奇頂點(連接的邊數量為奇數的頂點)的數目等於0或者2。
連通的無向圖 是歐拉環(存在歐拉迴路)的充要條件是:中每個頂點的度都是偶數。[2]。
- 必要性:如果一個圖能一筆畫成,那麼對每一個頂點,要麼路徑中「進入」這個點的邊數等於「離開」這個點的邊數:這時點的度為偶數。要麼兩者相差一:這時這個點必然是起點或終點之一。注意到有起點就必然有終點,因此奇頂點的數目要麼是0,要麼是2。
- 充分性:
- 如果圖中沒有奇頂點,那麼隨便選一個點出發,連一個環。如果這個環就是原圖,那麼結束。如果不是,那麼由於原圖是連通的, 和原圖的其它部分必然有公共頂點 。從這一點出發,在原圖的剩餘部分中重複上述步驟。由於原圖是連通圖,經過若干步後,全圖被分為一些環。由於兩個相連的環就是一個環,原來的圖也就是一個歐拉環了。
- 如果圖中有兩個奇頂點 和 ,那麼加多一條邊將它們連上後得到一個無奇頂點的連通圖。由上知這個圖是一個環,因此去掉新加的邊後成為一條路徑,起點和終點是 和 。證畢。
連通無向圖有歐拉路徑的充要條件也可以寫作「圖中奇頂點數目不多於2個」,這是因為奇頂點數目不可能是1個。實際上,連通無向圖中,奇頂點的數目總是偶數。
對於不連通的無向圖,如果有兩個互不連通的部分都包含至少一條邊,那麼顯然不能一筆畫。只有當此圖的邊全都在某一個連通部分中(即其它的連通部分都是一個個孤立的頂點,度數為0),並滿足連通無向圖關於一筆畫的充要條件,而該圖才能一筆畫。也即是說,可以一筆畫的(無向)圖如果不是連通圖,就必定是一個可以一筆畫的連通圖與若干個孤立頂點的組合。
除了用頂點的度數作為判定的充要條件,還可以用圖中邊的特性來作為歐拉迴路存在的判定準則。連通的無向圖 中存在歐拉迴路,等價於圖所有的邊可以劃分為若干個環的不交並。具體來說,等價於存在一系列的環,使得圖里的每一條邊都恰好屬於某一個環。
定理二[編輯]
如果連通無向圖 有 個奇頂點,那麼它可以用 筆畫成,並且至少要用 筆畫成[2]。
有向圖的一筆畫[編輯]
對有向圖來說,一筆畫不僅指遍歷所有邊,而且要遵循正確的方向。嚴謹地說,一個連通有向圖有歐拉路徑,指存在一個頂點,從它出發,沿着有向邊的方向,可以不重複地遍歷圖中所有的邊。有向圖的歐拉迴路則是指可以從某一頂點開始,沿有向邊的方向不重複地遍歷所有邊,然後回到原來出發的頂點。用類似於定理一中證明的思路,可以得到有向圖一筆畫的判定準則:
- 一個連通的有向圖可以表示為一條從頂點到的(不閉合的)歐拉路徑的充要條件是:的出度(從這個頂點發出的有向邊的數量)比入度(指向這個頂點的有向邊的數量)多1,的出度比入度少1,而其它頂點的出度和入度都相等。
- 一個連通的有向圖是歐拉環(存在歐拉迴路)的充要條件是以下兩個之一:
- 每個頂點的出度和入度都相等;
- 存在一系列的(有向)環,使得圖里的每一條邊都恰好屬於某一個環。
例子[編輯]
-
圖一:無法一筆畫,原因:有四個奇頂點,不符合0個或2個奇頂點的條件
-
圖二:儘管按照中文書寫習慣「串」字不止一筆,但它可以一筆寫成,因為只有上下兩個奇頂點。
-
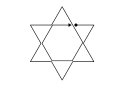
圖三:六角星,0個奇頂點
-
圖四,只有兩個在下方的奇頂點
-
圖五(圖四的動態版)
七橋問題[編輯]
圖一是七橋問題抽象化後得到的模型,由四個頂點和七條邊組成。由於四個頂點全是奇頂點,由定理一(奇頂點的數目正好是0個或2個)可知無法一筆畫成。
一些可以一筆畫的例子[編輯]
圖二是中文「串」字。由於只有最上方和最下方的頂點是奇頂點,由定理一知它可以一筆寫成,圖片內給出了一個例子。
圖三的六角星因每個頂點都是偶頂點,如上,由定理一得知,不論是由哪個點出發,它都可以一筆畫成。
圖四(和圖五)的圖只有最左下方和最右下方的頂點是奇頂點,由定理一知它可以一筆畫成,由其中一個奇頂點畫到另一個奇頂點。
一筆畫問題與哈密頓問題[編輯]
一筆畫問題討論的是能否不重複地遍歷一個圖的所有邊,至於其中有否頂點的遍歷或重複經過則沒有要求。哈密頓問題討論的則是頂點的遍歷:能否不重複地遍歷一個圖的所有頂點?[4]哈密頓問題由哈密頓在1856年首次提出,至今尚未完全解決[2]。