方波 的傅立葉級數前四項的部份總和。隨著增加更多的諧波,這個部份總和收斂成方波。在數學 中,傅立葉級數 (英語:Fourier series ,波 的函數表示成簡單諧波 的方式。更正式地說,對於滿足狄利克雷定理 的週期函數 ,其傅立葉級數 是由一組正弦 與餘弦函數 的加權 和表示的方法。傅立葉級數與用來找出無週期函數的頻率訊息的傅立葉轉換 有密切的關係。
傅立葉級數是傅立葉分析 的一個研究分支,也是取樣定理 原始證明的核心。傅立葉級數在數論 、組合數學 、訊號 處理、機率論 、統計學 、密碼學 、聲學 、光學 等領域都有著廣泛的應用。
傅立葉級數得名於法國數學家約瑟夫·傅立葉 (1768年–1830年),他提出任何 函數都可以展開 為三角級數 。此前數學家歐拉 、達朗貝爾 和克萊羅 ,已發現在認定一個函數有三角級數展開後,通過積分方法計算其係數的公式,而拉格朗日 等人已經找到了一些非週期函數的三角級數展開。將週期函數分解為簡單振盪 函數的總和的最早想法,可以追溯至公元前3世紀古代天文學家的均輪和本輪 學說。
傅立葉的工作得到了丹尼爾·伯努利 的贊助[1] 熱傳導方程式 ,其最初論文雖經西爾維斯特·拉克魯瓦 加斯帕爾·蒙日 同意[2] 拉格朗日 、拉普拉斯 和勒讓德 評審後被拒絕出版,他的現在被稱為傅里葉逆轉定理 [3]
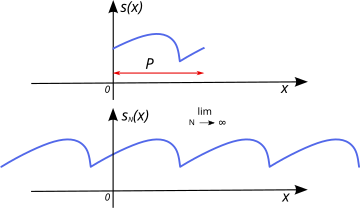
上圖展示了藍色無週期函數
s
(
x
)
{\displaystyle s(x)}
[
0
,
P
]
{\displaystyle [0,P]}
s
(
x
)
{\displaystyle s(x)}
傅立葉級數可以用不同的形式來表達,下面將週期 為
P
{\displaystyle P}
週期函數
s
(
x
)
,
x
∈
R
{\textstyle s(x),\ x\in \mathbb {R} }
正弦-餘弦形式 [ 編輯 ] 人們常用
sin
(
x
)
{\displaystyle \sin(x)}
cos
(
x
)
{\displaystyle \cos(x)}
三角級數 來表示
s
(
x
)
{\textstyle s(x)}
n
{\displaystyle n}
諧波
sin
(
2
π
n
x
P
)
{\textstyle \sin({\frac {2\pi nx}{P}})}
cos
(
2
π
n
x
P
)
{\textstyle \cos({\frac {2\pi nx}{P}})}
s
(
x
)
{\textstyle s(x)}
權重 ,求得它們的總和 ;這些
n
{\displaystyle n}
傅立葉級數係數
A
0
=
1
P
∫
P
s
(
x
)
d
x
A
n
=
2
P
∫
P
s
(
x
)
cos
(
2
π
n
x
P
)
d
x
for
n
≥
1
B
n
=
2
P
∫
P
s
(
x
)
sin
(
2
π
n
x
P
)
d
x
for
n
≥
1
{\displaystyle {\begin{aligned}A_{0}&={\frac {1}{P}}\int _{P}s(x)\,dx\\A_{n}&={\frac {2}{P}}\int _{P}s(x)\cos \left({\frac {2\pi nx}{P}}\right)\,dx\qquad {\text{for }}n\geq 1\qquad \\B_{n}&={\frac {2}{P}}\int _{P}s(x)\sin \left({\frac {2\pi nx}{P}}\right)\,dx\qquad {\text{for }}n\geq 1\end{aligned}}}
符號
∫
P
{\textstyle \int _{P}}
區間 上的積分,典型的選擇為
[
−
P
/
2
,
P
/
2
]
{\displaystyle [-P/2,P/2]}
[
0
,
P
]
{\displaystyle [0,P]}
A
0
{\displaystyle A_{0}}
s
(
x
)
{\displaystyle s(x)}
平均值 [A] 傅立葉轉換 。
通過這些係數定義傅立葉級數為:
傅立葉級數,正弦-餘弦形式
s
(
x
)
∼
A
0
+
∑
n
=
1
∞
(
A
n
cos
(
2
π
n
x
P
)
+
B
n
sin
(
2
π
n
x
P
)
)
{\displaystyle s(x)\sim A_{0}+\sum _{n=1}^{\infty }\left(A_{n}\cos \left({\frac {2\pi nx}{P}}\right)+B_{n}\sin \left({\frac {2\pi nx}{P}}\right)\right)}
這裡使用符號
∼
{\displaystyle \sim }
s
(
x
)
{\displaystyle s(x)}
n
{\displaystyle n}
x
{\displaystyle x}
s
(
x
)
{\textstyle s(x)}
Eq. 2
∼
{\displaystyle \sim }
=
{\displaystyle =}
在傅立葉級數係數中的整數索引
n
{\displaystyle n}
cos
{\displaystyle \cos }
sin
{\displaystyle \sin }
週期
P
{\displaystyle P}
圓周 (cycle)的數目。因此對應於
A
n
{\displaystyle A_{n}}
B
n
{\displaystyle B_{n}}
波長 等於
P
n
{\displaystyle {\tfrac {P}{n}}}
x
{\displaystyle x}
頻率 等於
n
P
{\displaystyle {\tfrac {n}{P}}}
x
{\displaystyle x}
指數形式 [ 編輯 ] 下面藉由歐拉公式
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle \ e^{ix}=\cos x+i\sin x\ }
複數 指數 形式。
根據定義,我們可以得到:
複數傅立葉級數係數
c
0
=
A
0
c
n
=
(
A
n
−
i
B
n
)
/
2
for
n
>
0
c
n
=
(
A
−
n
+
i
B
−
n
)
/
2
for
n
<
0
{\displaystyle {\begin{aligned}c_{0}&=A_{0}&\\c_{n}&=(A_{n}-iB_{n})/2\qquad &{\text{for }}n>0\\c_{n}&=(A_{-n}+iB_{-n})/2\qquad &{\text{for }}n<0\end{aligned}}}
通過將等式Eq. 1 Eq. 3 [4]
複數傅立葉級數係數
c
n
=
1
P
∫
P
s
(
x
)
e
−
2
π
i
n
x
P
d
x
for
n
∈
Z
{\displaystyle c_{n}={\frac {1}{P}}\int _{P}s(x)e^{-{\frac {2\pi inx}{P}}}\,dx\qquad {\text{for}}\ n\in \mathbb {Z} }
給定複數傅立葉級數係數,可以用公式復原出
A
n
{\displaystyle A_{n}}
B
n
{\displaystyle B_{n}}
複數傅立葉級數係數
A
0
=
c
0
A
n
=
c
n
+
c
−
n
for
n
>
0
B
n
=
i
(
c
n
−
c
−
n
)
for
n
>
0
{\displaystyle {\begin{aligned}A_{0}&=c_{0}&\\A_{n}&=c_{n}+c_{-n}\qquad &{\textrm {for}}~n>0\\B_{n}&=i(c_{n}-c_{-n})\qquad &{\textrm {for}}~n>0\end{aligned}}}
通過這些定義,傅立葉級數可以寫為:
傅立葉級數,指數形式
s
(
x
)
∼
∑
n
=
−
∞
∞
c
n
⋅
e
2
π
i
n
x
P
{\displaystyle s(x)\sim \sum _{n=-\infty }^{\infty }c_{n}\cdot e^{\frac {2\pi inx}{P}}}
這是可推廣到複數值域 函數的慣用形式。
n
{\displaystyle n}
負頻率 。
複數值函數 [ 編輯 ] 人們習慣將
s
(
x
)
{\textstyle s(x)}
值域 普遍化到複數 上,設
s
(
x
)
{\textstyle s(x)}
s
(
x
)
=
Re
(
s
(
x
)
)
+
i
⋅
Im
(
s
(
x
)
)
,
x
∈
R
{\displaystyle s(x)=\operatorname {Re} (s(x))+i\cdot \operatorname {Im} (s(x)),\quad x\in \mathbb {R} }
定義
c
n
≜
c
R
n
+
i
⋅
c
I
n
{\displaystyle c_{n}\triangleq c_{_{Rn}}+i\cdot c_{_{In}}}
c
n
=
1
P
∫
P
s
(
x
)
⋅
e
−
i
2
π
p
n
x
d
x
=
1
P
∫
P
Re
(
s
(
x
)
)
⋅
e
−
i
2
π
p
n
x
d
x
+
i
⋅
1
P
∫
P
Im
(
s
(
x
)
)
⋅
e
−
i
2
π
p
n
x
d
x
{\displaystyle c_{n}={\frac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx={\frac {1}{P}}\int _{P}\operatorname {Re} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx+i\cdot {\frac {1}{P}}\int _{P}\operatorname {Im} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}
c
R
n
=
1
P
∫
P
Re
(
s
(
x
)
)
⋅
e
−
i
2
π
p
n
x
d
x
{\displaystyle c_{_{Rn}}={\frac {1}{P}}\int _{P}\operatorname {Re} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}
c
I
n
=
1
P
∫
P
Im
(
s
(
x
)
)
⋅
e
−
i
2
π
p
n
x
d
x
{\displaystyle c_{_{In}}={\frac {1}{P}}\int _{P}\operatorname {Im} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}
對於這個複數值函數,它的傅立葉級數的實部,是它的實部的傅立葉級數;它的傅立葉級數的虛部,是它的虛部的傅立葉級數:
s
(
x
)
∼
∑
n
=
−
∞
∞
(
c
R
n
+
i
⋅
c
I
n
)
⋅
e
i
2
π
p
n
x
=
∑
n
=
∞
∞
c
R
n
⋅
e
i
2
π
p
n
x
+
i
⋅
∑
n
=
−
∞
∞
c
I
n
⋅
e
i
2
π
p
n
x
{\displaystyle s(x)\sim \sum _{n=-\infty }^{\infty }\left(c_{_{Rn}}+i\cdot c_{_{In}}\right)\cdot e^{i{\tfrac {2\pi }{p}}nx}=\sum _{n=\infty }^{\infty }c_{_{Rn}}\cdot e^{i{\tfrac {2\pi }{p}}nx}+i\cdot \sum _{n=-\infty }^{\infty }c_{_{In}}\cdot e^{i{\tfrac {2\pi }{p}}nx}}
振幅-相位形式 [ 編輯 ] 還可以利用三角恆等式
cos
(
α
−
β
)
=
cos
α
cos
β
+
sin
α
sin
β
{\displaystyle \ \cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta \,}
A
n
⋅
cos
(
2
π
n
P
x
−
φ
n
)
≡
A
n
cos
(
φ
n
)
⏟
a
n
⋅
cos
(
2
π
n
P
x
)
+
A
n
sin
(
φ
n
)
⏟
b
n
⋅
sin
(
2
π
n
P
x
)
{\displaystyle A_{n}\cdot \cos \left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)\ \equiv \ \underbrace {A_{n}\cos(\varphi _{n})} _{a_{n}}\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)+\underbrace {A_{n}\sin(\varphi _{n})} _{b_{n}}\cdot \sin \left(2\pi {\tfrac {n}{P}}x\right)}
然後定義振幅
A
n
≜
a
n
2
+
b
n
2
{\textstyle A_{n}\triangleq {\sqrt {a_{n}^{2}+b_{n}^{2}}}}
相位
φ
n
≜
arctan2
(
b
n
,
a
n
)
{\textstyle \varphi _{n}\triangleq \operatorname {arctan2} (b_{n},a_{n})}
a
n
{\displaystyle a_{n}}
b
n
{\displaystyle b_{n}}
A
n
{\displaystyle A_{n}}
B
n
{\displaystyle B_{n}}
A
0
2
{\displaystyle {\tfrac {A_{0}}{2}}}
s
(
x
)
{\displaystyle s(x)}
平均值
1
P
∫
P
s
(
x
)
d
x
{\textstyle {\frac {1}{P}}\int _{P}s(x)\,dx}
傅立葉級數,振幅-相位形式
s
(
x
)
∼
A
0
2
+
∑
n
=
1
∞
A
n
⋅
cos
(
2
π
n
P
x
−
φ
n
)
{\displaystyle s(x)\sim {\frac {A_{0}}{2}}+\sum _{n=1}^{\infty }A_{n}\cdot \cos \left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)}
部份求和算子 [ 編輯 ] 在描述傅立葉級數行為的時候,經常會為一個函數
f
(
x
)
{\displaystyle f(x)}
部份求和 算子
S
N
{\displaystyle S_{N}}
[5]
S
N
(
f
)
=
∑
n
=
−
N
N
c
n
e
2
π
i
n
x
P
{\displaystyle S_{N}(f)=\sum _{n=-N}^{N}c_{n}e^{\frac {2\pi inx}{P}}}
這裡的
c
n
{\displaystyle c_{n}}
f
{\displaystyle f}
假設
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
R
{\textstyle \mathbb {R} }
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
[
−
π
,
π
]
{\displaystyle [-\pi ,\pi ]}
捲積
(
f
∗
g
)
(
x
)
{\displaystyle (f*g)(x)}
(
f
∗
g
)
(
x
)
=
∫
−
π
π
f
(
τ
)
g
(
x
−
τ
)
d
τ
{\displaystyle (f*g)(x)=\int _{-\pi }^{\pi }f(\tau )g(x-\tau )d\tau }
週期為
2
π
{\displaystyle 2\pi }
f
(
x
)
{\displaystyle f(x)}
部份求和 ,可以經由
f
(
x
)
{\displaystyle f(x)}
狄利克雷核
D
n
(
x
)
=
∑
k
=
−
n
n
e
i
k
x
{\textstyle D_{n}(x)=\sum _{k=-n}^{n}e^{ikx}}
摺積 來表示:
S
N
(
f
)
(
x
)
=
∑
n
=
−
N
N
c
n
e
i
n
x
=
∑
n
=
−
N
N
(
1
2
π
∫
−
π
π
f
(
τ
)
e
−
i
n
τ
d
τ
)
⋅
e
i
n
x
=
1
2
π
∫
−
π
π
f
(
τ
)
(
∑
n
=
−
N
N
e
i
n
(
x
−
τ
)
)
d
τ
=
1
2
π
(
f
∗
D
N
)
(
x
)
{\displaystyle {\begin{aligned}S_{N}(f)(x)&=\sum _{n=-N}^{N}c_{n}e^{inx}\\&=\sum _{n=-N}^{N}\left({\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(\tau )e^{-in\tau }d\tau \right)\cdot e^{inx}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(\tau )\left(\sum _{n=-N}^{N}e^{in(x-\tau )}\right)d\tau \\&={\frac {1}{2\pi }}(f*D_{N})(x)\end{aligned}}}
收斂性概要 [ 編輯 ]
s
N
(
x
)
{\displaystyle s_{N}(x)}
[
x
0
,
x
0
+
P
]
{\displaystyle [x_{0},\ x_{0}+P]}
s
(
x
)
{\displaystyle s(x)}
N
→
∞
{\displaystyle N\rightarrow \infty }
無窮和
s
∞
(
x
)
{\displaystyle s_{\infty }(x)}
s
{\displaystyle s}
狄利克雷條件 。參見傅立葉級數的收斂性 弱收斂
s
(
x
)
{\displaystyle s(x)}
不可導 點上,如果我們只取無窮級數中的有限項求和,那麼在這些點上會有幅度不隨
N
{\displaystyle N}
吉布斯現象 ,一個簡單的例子是方波訊號 。
在工程 應用中,一般假定傅立葉級數除了在不連續點以外處處收斂,原因是工程上遇到的函數比數學家提供的這個假定的反例表現更加良好。特別地,傅立葉級數絕對收斂 且均勻收斂 於
s
(
x
)
{\displaystyle s(x)}
s
(
x
)
{\displaystyle s(x)}
[6]
[
x
0
,
x
0
+
P
]
{\displaystyle [x_{0},x_{0}+P]}
平方可積 的,那麼此傅立葉級數在幾乎處處 的點都收斂於該函數。
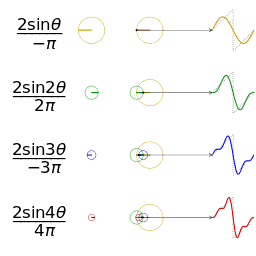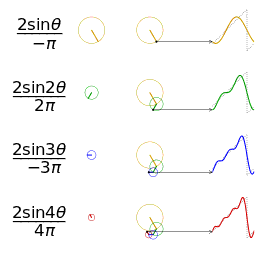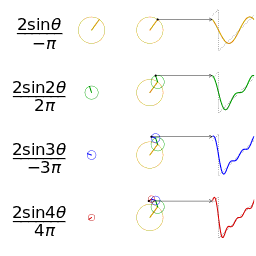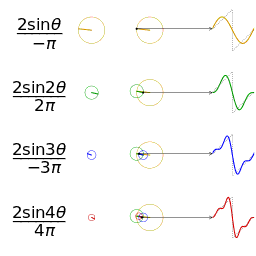
一個相同幅度和頻率的鋸齒波的近似的可視化
另一個分別採用傅立葉級數的前 1, 2, 3, 4 項近似方波的可視化。(可以在這裡
[7] 看到一個交互式的動畫)
其他常用表示法 [ 編輯 ] 符號
c
n
{\displaystyle c_{n}}
s
{\displaystyle s}
s
^
[
n
]
{\displaystyle {\hat {s}}[n]}
S
[
n
]
{\displaystyle S[n]}
s
(
x
)
=
∑
n
=
−
∞
∞
s
^
(
n
)
⋅
e
2
π
i
n
x
/
P
{\displaystyle s(x)=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{2\pi inx/P}\quad }
s
(
x
)
=
∑
n
=
−
∞
∞
S
[
n
]
⋅
e
i
2
π
n
x
/
P
{\displaystyle s(x)=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\quad }
在工程上,特別是在變量
x
{\displaystyle x}
頻域 表示。經常使用方括號來強調這個函數的定義域是頻率 的離散集合。
另一個常用頻域表示,使用傅立葉級數係數,調製 像梳子一樣的狄拉克取樣函數
S
(
f
)
≜
∑
n
=
−
∞
∞
S
[
n
]
⋅
δ
(
f
−
n
P
)
{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)}
這裡的
f
{\displaystyle f}
x
{\displaystyle x}
f
{\displaystyle f}
赫茲 為單位。取樣的間隔為基本頻率
1
P
{\displaystyle {\tfrac {1}{P}}}
n
{\displaystyle n}
諧波 )。
s
∞
(
x
)
{\displaystyle s_{\infty }(x)}
逆傅立葉轉換
F
−
1
{
S
(
f
)
}
=
∫
−
∞
∞
(
∑
n
=
−
∞
∞
S
[
n
]
⋅
δ
(
f
−
n
P
)
)
e
i
2
π
f
x
d
f
=
∑
n
=
−
∞
∞
S
[
n
]
⋅
∫
−
∞
∞
δ
(
f
−
n
P
)
e
i
2
π
f
x
d
f
=
∑
n
=
−
∞
∞
S
[
n
]
⋅
e
i
2
π
n
x
/
P
≜
s
∞
(
x
)
{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x)\end{aligned}}}
構造出的函數
S
(
f
)
{\displaystyle S(f)}
傅立葉轉換 」,即使一個週期函數的傅立葉積分在這個諧波頻率上不收斂[B]
常用的傅立葉級數 [ 編輯 ] 下表列出常用的週期函數及其傅立葉級數係數。
s
(
x
)
{\displaystyle s(x)}
P
{\displaystyle P}
A
0
{\displaystyle A_{0}}
A
n
{\displaystyle A_{n}}
B
n
{\displaystyle B_{n}}
s
(
x
)
{\displaystyle s(x)}
時域
s
(
x
)
{\displaystyle s(x)}
繪圖
頻域(正弦-餘弦形式)
A
0
A
n
for
n
≥
1
B
n
for
n
≥
1
{\displaystyle {\begin{aligned}&A_{0}\\&A_{n}\quad {\text{for }}n\geq 1\\&B_{n}\quad {\text{for }}n\geq 1\end{aligned}}}
注釋
引用
s
(
x
)
=
A
|
sin
(
2
π
P
x
)
|
for
0
≤
x
<
P
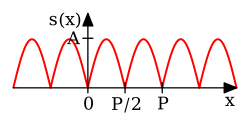
{\displaystyle s(x)=A\left|\sin \left({\frac {2\pi }{P}}x\right)\right|\quad {\text{for }}0\leq x<P}
A
0
=
2
A
π
A
n
=
{
−
4
A
π
1
n
2
−
1
n
even
0
n
odd
B
n
=
0
{\displaystyle {\begin{aligned}A_{0}=&{\frac {2A}{\pi }}\\A_{n}=&{\begin{cases}{\frac {-4A}{\pi }}{\frac {1}{n^{2}-1}}&\quad n{\text{ even}}\\0&\quad n{\text{ odd}}\end{cases}}\\B_{n}=&0\\\end{aligned}}}
全波整流正弦
[8] :p. 193
s
(
x
)
=
{
A
sin
(
2
π
P
x
)
for
0
≤
x
<
P
/
2
0
for
P
/
2
≤
x
<
P
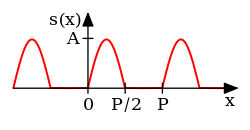
{\displaystyle s(x)={\begin{cases}A\sin \left({\frac {2\pi }{P}}x\right)&\quad {\text{for }}0\leq x<P/2\\0&\quad {\text{for }}P/2\leq x<P\\\end{cases}}}
A
0
=
A
π
A
n
=
{
−
2
A
π
1
n
2
−
1
n
even
0
n
odd
B
n
=
{
A
2
n
=
1
0
n
>
1
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{\pi }}\\A_{n}=&{\begin{cases}{\frac {-2A}{\pi }}{\frac {1}{n^{2}-1}}&\quad n{\text{ even}}\\0&\quad n{\text{ odd}}\end{cases}}\\B_{n}=&{\begin{cases}{\frac {A}{2}}&\quad n=1\\0&\quad n>1\end{cases}}\\\end{aligned}}}
半波整流正弦
[8] :p. 193
s
(
x
)
=
{
A
for
0
≤
x
<
D
⋅
P
0
for
D
⋅
P
≤
x
<
P
{\displaystyle s(x)={\begin{cases}A&\quad {\text{for }}0\leq x<D\cdot P\\0&\quad {\text{for }}D\cdot P\leq x<P\\\end{cases}}}
A
0
=
A
D
A
n
=
A
n
π
sin
(
2
π
n
D
)
B
n
=
2
A
n
π
(
sin
(
π
n
D
)
)
2
{\displaystyle {\begin{aligned}A_{0}=&AD\\A_{n}=&{\frac {A}{n\pi }}\sin \left(2\pi nD\right)\\B_{n}=&{\frac {2A}{n\pi }}\left(\sin \left(\pi nD\right)\right)^{2}\\\end{aligned}}}
0
≤
D
≤
1
{\displaystyle 0\leq D\leq 1}
s
(
x
)
=
A
x
P
for
0
≤
x
<
P
{\displaystyle s(x)={\frac {Ax}{P}}\quad {\text{for }}0\leq x<P}
A
0
=
A
2
A
n
=
0
B
n
=
−
A
n
π
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{2}}\\A_{n}=&0\\B_{n}=&{\frac {-A}{n\pi }}\\\end{aligned}}}
[8] :p. 192
s
(
x
)
=
A
−
A
x
P
for
0
≤
x
<
P
{\displaystyle s(x)=A-{\frac {Ax}{P}}\quad {\text{for }}0\leq x<P}
A
0
=
A
2
A
n
=
0
B
n
=
A
n
π
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{2}}\\A_{n}=&0\\B_{n}=&{\frac {A}{n\pi }}\\\end{aligned}}}
[8] :p. 192
s
(
x
)
=
4
A
P
2
(
x
−
P
2
)
2
for
0
≤
x
<
P
{\displaystyle s(x)={\frac {4A}{P^{2}}}\left(x-{\frac {P}{2}}\right)^{2}\quad {\text{for }}0\leq x<P}
A
0
=
A
3
A
n
=
4
A
π
2
n
2
B
n
=
0
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{3}}\\A_{n}=&{\frac {4A}{\pi ^{2}n^{2}}}\\B_{n}=&0\\\end{aligned}}}
[8] :p. 193
基本性質 [ 編輯 ] 下表展示在時域中的一些數學運算及其對應的在傅立葉級數係數上的效果。
複數共軛 指示為上標星號
∗
{\displaystyle \ ^{*}\ }
s
(
x
)
{\displaystyle s(x)}
r
(
x
)
{\displaystyle r(x)}
P
{\displaystyle P}
x
∈
[
0
,
P
]
{\displaystyle x\in [0,P]}
S
[
n
]
{\displaystyle S[n]}
R
[
n
]
{\displaystyle R[n]}
s
{\displaystyle s}
r
{\displaystyle r}
性質
時域
頻域(指數形式)
注釋
引用
線性
a
⋅
s
(
x
)
+
b
⋅
r
(
x
)
{\displaystyle a\cdot s(x)+b\cdot r(x)}
a
⋅
S
[
n
]
+
b
⋅
R
[
n
]
{\displaystyle a\cdot S[n]+b\cdot R[n]}
a
,
b
∈
C
{\displaystyle a,b\in \mathbb {C} }
時間反轉/頻率反轉
s
(
−
x
)
{\displaystyle s(-x)}
S
[
−
n
]
{\displaystyle S[-n]}
[9] :p. 610
時間共軛
s
∗
(
x
)
{\displaystyle s^{*}(x)}
S
∗
[
−
n
]
{\displaystyle S^{*}[-n]}
[9] :p. 610
時間反轉且共軛
s
∗
(
−
x
)
{\displaystyle s^{*}(-x)}
S
∗
[
n
]
{\displaystyle S^{*}[n]}
時間實部
Re
(
s
(
x
)
)
{\displaystyle \operatorname {Re} {(s(x))}}
1
2
(
S
[
n
]
+
S
∗
[
−
n
]
)
{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}
時間虛部
Im
(
s
(
x
)
)
{\displaystyle \operatorname {Im} {(s(x))}}
1
2
i
(
S
[
n
]
−
S
∗
[
−
n
]
)
{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}
頻率實部
1
2
(
s
(
x
)
+
s
∗
(
−
x
)
)
{\displaystyle {\frac {1}{2}}(s(x)+s^{*}(-x))}
Re
(
S
[
n
]
)
{\displaystyle \operatorname {Re} {(S[n])}}
頻率虛部
1
2
i
(
s
(
x
)
−
s
∗
(
−
x
)
)
{\displaystyle {\frac {1}{2i}}(s(x)-s^{*}(-x))}
Im
(
S
[
n
]
)
{\displaystyle \operatorname {Im} {(S[n])}}
時間移位/頻率調製
s
(
x
−
x
0
)
{\displaystyle s(x-x_{0})}
S
[
n
]
⋅
e
−
i
2
π
P
n
x
0
{\displaystyle S[n]\cdot e^{-i{\frac {2\pi }{P}}nx_{0}}}
x
0
∈
R
{\displaystyle x_{0}\in \mathbb {R} }
[9] :p. 610
頻率移位/時間調製
s
(
x
)
⋅
e
i
2
π
P
n
0
x
{\displaystyle s(x)\cdot e^{i{\frac {2\pi }{P}}n_{0}x}}
S
[
n
−
n
0
]
{\displaystyle S[n-n_{0}]\!}
n
0
∈
Z
{\displaystyle n_{0}\in \mathbb {Z} }
[9] :p. 610
對稱性質 [ 編輯 ] 所有的函數都可以分解成唯一性的偶部和奇部
f
(
x
)
=
f
e
(
x
)
+
f
o
(
x
)
{\displaystyle f(x)=f_{\text{e}}(x)+f_{\text{o}}(x)}
f
e
(
x
)
=
f
(
x
)
+
f
(
−
x
)
2
{\textstyle f_{\text{e}}(x)={\frac {f(x)+f(-x)}{2}}}
f
o
(
x
)
=
f
(
x
)
−
f
(
−
x
)
2
{\textstyle f_{\text{o}}(x)={\frac {f(x)-f(-x)}{2}}}
f
:
R
→
C
{\displaystyle f:\mathbb {R} \to \mathbb {C} }
x
∈
R
{\displaystyle x\in \mathbb {R} }
f
(
x
)
=
f
(
−
x
)
¯
{\displaystyle f(x)={\overline {f(-x)}}}
f
(
x
)
=
−
f
(
−
x
)
¯
{\displaystyle f(x)=-{\overline {f(-x)}}}
z
¯
{\displaystyle {\overline {z}}}
複數共軛 。
一個複數值函數的實部和虛部,分解成各自的偶部和奇部,就有了四個分量,分別用下標標明為RE、RO、IE和IO。一個複數值時間參數函數的四個分量,與它的複數頻率轉換的四個分量之間,有著一一映射[10]
时 域
s
=
s
RE
+
s
RO
+
i
s
IE
+
i
s
IO
⇕
F
⇕
F
⇕
F
⇕
F
⇕
F
频 域
S
=
S
RE
+
i
S
IO
+
i
S
IE
+
S
RO
{\displaystyle {\begin{array}{rccccccccc}{\text{时 域}}&s&=&s_{_{\text{RE}}}&+&s_{_{\text{RO}}}&+&i\ s_{_{\text{IE}}}&+&i\ s_{_{\text{IO}}}\\&{\Bigg \Updownarrow }{\mathcal {F}}&&{\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}\\{\text{频 域}}&S&=&S_{\text{RE}}&+&\,i\ S_{\text{IO}}\,&+&i\ S_{\text{IE}}&+&S_{\text{RO}}\end{array}}}
由此可見,各種關係是顯而易見的,例如:
實數值函數s RE s RO S RE i S IO
虛數值函數i s IE i s IO S RO i S IE
偶對稱函數s RE i s IO S RE S RO
奇對稱函數s RO i s IE i S IE i S IO 一個簡單的傅立葉級數 [ 編輯 ] 鋸齒波 週期函數的圖前五個部分傅立葉級數的動態圖 我們現在用上面的公式給出一個簡單函數的傅立葉級數展開式。考慮一個鋸齒波:
s
(
x
)
=
x
π
,
f
o
r
−
π
<
x
<
π
{\displaystyle s(x)={\frac {x}{\pi }},\quad \mathrm {for} -\pi <x<\pi }
s
(
x
+
2
π
k
)
=
s
(
x
)
,
f
o
r
−
∞
<
x
<
∞
and
k
∈
Z
{\displaystyle s(x+2\pi k)=s(x),\quad \mathrm {for} -\infty <x<\infty {\text{ and }}k\in \mathbb {Z} }
在這種情況下,傅立葉級數為:
A
n
=
1
π
∫
−
π
π
s
(
x
)
cos
(
n
x
)
d
x
=
0
,
n
≥
0
B
n
=
1
π
∫
−
π
π
s
(
x
)
sin
(
n
x
)
d
x
=
−
2
π
n
cos
(
n
π
)
+
2
π
2
n
2
sin
(
n
π
)
=
2
(
−
1
)
n
+
1
π
n
,
n
≥
1
{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1\end{aligned}}}
可以證明,當
s
{\displaystyle s}
x
{\displaystyle x}
s
(
x
)
{\displaystyle s(x)}
s
(
x
)
=
A
0
+
∑
n
=
1
∞
(
A
n
cos
(
n
x
)
+
B
n
sin
(
n
x
)
)
=
2
π
∑
n
=
1
∞
(
−
1
)
n
+
1
n
sin
(
n
x
)
,
f
o
r
x
−
π
∉
2
π
Z
{\displaystyle {\begin{aligned}s(x)&=A_{0}+\sum _{n=1}^{\infty }\left(A_{n}\cos \left(nx\right)+B_{n}\sin \left(nx\right)\right)\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} \end{aligned}}}
當
x
=
π
{\displaystyle x=\pi }
0
{\displaystyle 0}
x
=
π
{\displaystyle x=\pi }
s
{\displaystyle s}
狄利克雷定理 的特例。
這個例子為我們引出了巴塞爾問題 的一種解法。
傅立葉誘導 [ 編輯 ] 金屬板內的熱分布,使用傅立葉方法求解 在上例中我們的函數的傅立葉級數展開式看起來不比
s
(
x
)
=
x
π
{\displaystyle s(x)={\tfrac {x}{\pi }}}
熱方程式 的例子。考慮邊長為
π
{\displaystyle \pi }
(
x
,
y
)
∈
[
0
,
π
]
×
[
0
,
π
]
{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}
0
{\displaystyle 0}
y
=
π
{\displaystyle y=\pi }
x
∈
(
0
,
π
)
{\displaystyle x\in (0,\pi )}
T
(
x
,
π
)
=
x
{\displaystyle T(x,\pi )=x}
T
(
x
,
y
)
{\displaystyle T(x,y)}
解析解 ,但卻可以證明:
T
(
x
,
y
)
=
2
∑
n
=
1
∞
(
−
1
)
n
+
1
n
sin
(
n
x
)
sinh
(
n
y
)
sinh
(
n
π
)
{\displaystyle T(x,y)=2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx){\sinh(ny) \over \sinh(n\pi )}}
這裡的
sinh
{\displaystyle \sinh }
雙曲正弦 函數。熱方程式的這個解是通過將
π
s
(
x
)
{\displaystyle \pi s(x)}
sinh
(
n
y
)
sinh
(
n
π
)
{\displaystyle {\tfrac {\sinh(ny)}{\sinh(n\pi )}}}
s
(
x
)
{\displaystyle s(x)}
其他例子 [ 編輯 ] 我們也可以應用傅立葉級數去證明等周不等式 ,或是構造處處連續處處不可微的函數。
收斂性 [ 編輯 ] 至今還沒有判斷傅立葉級數的收斂性充分必要條件,但是對於實際問題中出現的函數,有很多種判別條件可用於判斷收斂性。比如
x
(
t
)
{\displaystyle x(t)}
均勻收斂性 。在閉區間上滿足狄利克雷條件 的函數表示成的傅立葉級數都收斂。狄利克雷條件如下:
在定義區間上,
x
(
t
)
{\displaystyle x(t)}
絕對可積 ;
在任一有限區間中,
x
(
t
)
{\displaystyle x(t)}
在任何有限區間上,
x
(
t
)
{\displaystyle x(t)}
第一類間斷點 。 滿足以上條件的
x
(
t
)
{\displaystyle x(t)}
1.當
t
{\displaystyle t}
x
(
t
)
{\displaystyle x(t)}
x
(
t
)
{\displaystyle x(t)}
2.當
t
{\displaystyle t}
x
(
t
)
{\displaystyle x(t)}
1
2
[
x
(
t
−
)
+
x
(
t
+
)
]
{\displaystyle {\frac {1}{2}}[x(t^{-})+x(t^{+})]}
1966年,里納特·卡爾松 證明了勒貝格二次可積 函數的傅立葉級數一定是幾乎處處收斂的,即級數在除了一個勒貝格零測集外均收斂。
傅立葉級數收斂證明 [ 編輯 ] 假設一個函數在
f
(
x
)
{\displaystyle f(x)}
[
0
,
2
π
]
{\displaystyle [0,2\pi ]}
1
2
π
∫
0
2
π
|
f
(
x
)
−
S
N
(
f
)
(
x
)
|
2
d
x
→
0
{\displaystyle {\frac {1}{2\pi }}\int _{0}^{2\pi }|f(x)-S_{N}(f)(x)|^{2}dx\rightarrow 0}
N
→
∞
{\displaystyle N\rightarrow \infty }
證明的第一步:
考慮一系列正交基底,
{
e
n
}
n
∈
Z
{\displaystyle \{e_{n}\}_{n\in \mathbb {Z} }}
e
n
(
x
)
=
e
−
i
n
x
{\displaystyle e_{n}(x)=e^{-inx}}
(
e
n
,
e
m
)
=
{
1
,
if
n
=
m
0
,
if
n
≠
m
{\displaystyle (e_{n},e_{m})={\begin{cases}1,&{\text{if }}n=m\\0,&{\text{if }}n\neq m\end{cases}}}
然後有
(
f
,
e
n
)
=
1
2
π
∫
0
2
π
f
(
x
)
e
−
i
n
x
d
x
=
f
^
(
n
)
{\displaystyle (f,e_{n})={\frac {1}{2\pi }}\int _{0}^{2\pi }f(x)e^{-inx}dx={\hat {f}}(n)}
特別的有,
f
(
x
)
{\displaystyle f(x)}
S
N
(
f
)
(
x
)
=
∑
|
n
|
≤
N
f
^
(
n
)
e
n
{\displaystyle S_{N}(f)(x)=\sum _{|n|\leq N}{\hat {f}}(n)e_{n}}
然後根據
f
=
f
−
∑
|
n
|
≤
N
f
^
(
n
)
e
n
+
∑
|
n
|
≤
N
f
^
(
n
)
e
n
{\displaystyle f=f-\sum _{|n|\leq N}{\hat {f}}(n)e_{n}+\sum _{|n|\leq N}{\hat {f}}(n)e_{n}}
|
|
f
|
|
2
=
|
|
f
−
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
+
|
|
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
{\displaystyle ||f||^{2}=||f-\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}+||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}}
|
|
f
|
|
2
=
|
|
f
−
S
N
(
f
)
(
x
)
|
|
2
+
|
|
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
{\displaystyle ||f||^{2}=||f-S_{N}(f)(x)||^{2}+||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}}
如果右邊第一項收斂到0,再根據正交的性質,可以看出上述式子中的右手邊第二項:
|
|
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
=
∑
|
n
|
≤
N
|
f
^
(
n
)
|
2
{\displaystyle ||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}=\sum _{|n|\leq N}|{\hat {f}}(n)|^{2}}
帕塞瓦爾定理 。證明的第二步:
回到證明右邊第一項,因為函數
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
|
f
−
S
N
(
f
)
(
x
)
|
≤
|
f
(
x
)
−
g
(
x
)
|
+
|
g
(
x
)
−
S
N
(
f
)
(
x
)
|
{\displaystyle |f-S_{N}(f)(x)|\leq |f(x)-g(x)|+|g(x)-S_{N}(f)(x)|}
故當
N
→
∞
{\displaystyle N\rightarrow \infty }
f
(
x
)
{\displaystyle f(x)}
S
N
(
f
)
(
x
)
{\displaystyle S_{N}(f)(x)}
其他性質 [ 編輯 ] 傅立葉級數的唯一性 [ 編輯 ] 如果有一個定義在
[
−
π
,
π
]
{\displaystyle [-\pi ,\pi ]}
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
f
^
(
n
)
{\displaystyle {\hat {f}}(n)}
g
^
(
n
)
{\displaystyle {\hat {g}}(n)}
f
(
x
)
=
g
(
x
)
{\displaystyle f(x)=g(x)}
f
(
x
)
{\displaystyle f(x)}
[
−
π
,
π
]
{\displaystyle [-\pi ,\pi ]}
f
^
(
n
)
{\displaystyle {\hat {f}}(n)}
n
∈
N
{\displaystyle n\in \mathbb {N} }
f
(
x
)
=
0
{\displaystyle f(x)=0}
摺積定理 [ 編輯 ] 給定週期為
P
{\displaystyle P}
s
P
{\displaystyle s_{_{P}}}
r
P
{\displaystyle r_{_{P}}}
S
[
n
]
{\displaystyle S[n]}
R
[
n
]
{\displaystyle R[n]}
n
∈
Z
{\displaystyle n\in \mathbb {Z} }
逐點乘積
h
P
(
x
)
≜
s
P
(
x
)
⋅
r
P
(
x
)
{\displaystyle h_{_{P}}(x)\triangleq s_{_{P}}(x)\cdot r_{_{P}}(x)}
P
{\displaystyle P}
S
{\displaystyle S}
R
{\displaystyle R}
離散摺積 :
H
[
n
]
=
(
S
∗
R
)
[
n
]
{\displaystyle H[n]=(S*R)[n]}
週期摺積
h
P
(
x
)
≜
(
s
P
∗
r
)
(
x
)
=
(
s
∗
r
P
)
(
x
)
=
∫
P
s
P
(
τ
)
⋅
r
P
(
x
−
τ
)
d
τ
{\textstyle h_{_{P}}(x)\triangleq (s_{_{P}}*r)(x)=(s*r_{_{P}})(x)=\int _{P}s_{_{P}}(\tau )\cdot r_{_{P}}(x-\tau )\,d\tau }
P
{\displaystyle P}
H
[
n
]
=
P
⋅
S
[
n
]
⋅
R
[
n
]
{\displaystyle H[n]=P\cdot S[n]\cdot R[n]}
在
c
0
(
Z
)
{\displaystyle c_{0}(\mathbb {Z} )}
雙無限序列
{
c
n
}
n
∈
Z
{\displaystyle \left\{c_{n}\right\}_{n\in Z}}
L
1
(
[
0
,
2
π
]
)
{\displaystyle L^{1}([0,2\pi ])}
ℓ
2
(
Z
)
{\displaystyle \ell ^{2}(\mathbb {Z} )}
摺積 [11] 微分性質 [ 編輯 ] 我們說
f
(
x
)
{\displaystyle f(x)}
C
k
(
T
)
{\displaystyle C^{k}(\mathbb {T} )}
⇒
{\displaystyle \Rightarrow }
f
(
x
)
{\displaystyle f(x)}
2
π
{\displaystyle 2\pi }
k
{\displaystyle k}
k
{\displaystyle k}
如果
f
(
x
)
{\displaystyle f(x)}
C
1
(
T
)
{\displaystyle C^{1}(\mathbb {T} )}
f
′
(
x
)
{\displaystyle f'(x)}
f
′
^
(
n
)
{\displaystyle {\hat {f'}}(n)}
f
(
x
)
{\displaystyle f(x)}
f
^
(
n
)
{\displaystyle {\hat {f}}(n)}
f
′
^
(
n
)
=
i
n
f
^
(
n
)
{\displaystyle {\hat {f'}}(n)=in{\hat {f}}(n)}
如果
f
(
x
)
{\displaystyle f(x)}
C
k
(
T
)
{\displaystyle C^{k}(\mathbb {T} )}
f
(
k
)
^
(
n
)
=
(
i
n
)
k
f
^
(
n
)
{\displaystyle {\hat {f^{(k)}}}(n)=(in)^{k}{\hat {f}}(n)}
k
≥
1
{\displaystyle k\geq 1}
f
(
k
)
^
(
n
)
{\displaystyle {\hat {f^{(k)}}}(n)}
n
→
∞
{\displaystyle n\rightarrow \infty }
f
(
k
)
^
(
n
)
=
O
(
1
/
n
k
)
{\displaystyle {\hat {f^{(k)}}}(n)=O(1/n^{k})}
黎曼-勒貝格定理 [ 編輯 ] 如果
S
{\displaystyle S}
可積函數 ,則
lim
|
n
|
→
∞
S
[
n
]
=
0
{\textstyle \lim _{|n|\to \infty }S[n]=0}
lim
n
→
+
∞
a
n
=
0
{\textstyle \lim _{n\to +\infty }a_{n}=0}
lim
n
→
+
∞
b
n
=
0
{\textstyle \lim _{n\to +\infty }b_{n}=0}
帕塞瓦爾定理 [ 編輯 ] 如果函數
f
(
x
)
{\displaystyle f(x)}
L
2
(
[
−
π
,
π
]
)
{\displaystyle L^{2}([-\pi ,\pi ])}
∑
−
∞
∞
|
f
^
(
n
)
|
2
=
1
2
π
∫
−
π
π
|
f
(
x
)
|
2
d
x
=
|
|
f
|
|
{\textstyle \sum _{-\infty }^{\infty }|{\hat {f}}(n)|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}dx=||f||}
普朗歇爾定理 [ 編輯 ] 如果
c
0
,
c
±
1
,
c
±
2
,
…
{\displaystyle c_{0},\,c_{\pm 1},\,c_{\pm 2},\ldots }
∑
n
=
−
∞
∞
|
c
n
|
2
<
∞
{\textstyle \sum _{n=-\infty }^{\infty }|c_{n}|^{2}<\infty }
s
∈
L
2
(
P
)
{\displaystyle s\in L^{2}(P)}
n
{\displaystyle n}
S
[
n
]
=
c
n
{\displaystyle S[n]=c_{n}}
希爾伯特空間的解讀 [ 編輯 ] 正弦和餘弦形成了正交集合。正弦、餘弦及其乘積的積分,當m 與n 不同或二函數不同時是0(綠色和紅色區域相等抵消),唯若m 和n 相等並且函數相同時為π。 所謂的兩個不同向量 正交是指它們的內積 為0,這也就意味著這兩個向量之間沒有任何相關性,例如,在三維歐氏空間中,互相垂直的向量之間是正交的。事實上,正交是垂直在數學上的一種抽象化和一般化。一組n個互相正交的向量必然是線性獨立 的,所以必然可以張成一個n維空間,也就是說,空間中的任何一個向量可以用它們來線性表出。
在希爾伯特空間 釋義下,函數的集合{en = einx ; n ∈ Z }是[−π, π]平方可積函數L 2 ([−π, π])的正交基 。這個空間實際上是一個希爾伯特空間,有著針對任何兩個的元素f 和g 的如下內積:
⟨
f
,
g
⟩
=
d
e
f
1
2
π
∫
−
π
π
f
(
x
)
g
(
x
)
¯
d
x
.
{\displaystyle \langle f,\,g\rangle \;{\stackrel {\mathrm {def} }{=}}\;{\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x){\overline {g(x)}}\,dx.}
三角函數族的正交性用公式表示出來就是:
∫
−
π
π
cos
(
m
x
)
cos
(
n
x
)
d
x
=
π
δ
m
n
,
m
,
n
≥
1
,
{\displaystyle \int _{-\pi }^{\pi }\cos(mx)\,\cos(nx)\,dx=\pi \delta _{mn},\quad m,n\geq 1,\,}
∫
−
π
π
sin
(
m
x
)
sin
(
n
x
)
d
x
=
π
δ
m
n
,
m
,
n
≥
1
{\displaystyle \int _{-\pi }^{\pi }\sin(mx)\,\sin(nx)\,dx=\pi \delta _{mn},\quad m,n\geq 1}
(這裡的δmn 克羅內克函數 ),而
∫
−
π
π
cos
(
m
x
)
sin
(
n
x
)
d
x
=
0
;
{\displaystyle \int _{-\pi }^{\pi }\cos(mx)\,\sin(nx)\,dx=0;\,}
^ 一些作者定義了與此不同的
A
0
{\displaystyle A_{0}}
A
0
{\displaystyle A_{0}}
A
n
{\displaystyle A_{n}}
Eq. 2
2
{\displaystyle 2}
^ 因為週期函數的傅立葉轉換的積分定義不是收斂的,需要將週期函數和它的轉換視為分布 。在這種意義上,
F
{
e
i
2
π
n
x
P
}
{\displaystyle {\mathcal {F}}\{e^{i{\frac {2\pi nx}{P}}}\}}
狄拉克δ函數 ,它是分布的是例子。
^ 詳見莫里斯·克萊因 《古今數學思想》,第20章無窮級數,第5節三角級數;第28章十九世紀的偏微分方程式,第5節熱方程式與傅立葉級數。see here, pg.s 209 & 210, (頁面存檔備份 ,存於網際網路檔案館 )
^ 李狗嗨. 如何给文科生解释傅里叶变换? . 知乎專欄. 2019-07-25 [2020-02-07 ] . (原始內容存檔 於2020-10-24) (中文) . ^ Théorie analytique de la chaleur . Paris: Firmin Didot Père et Fils. 1822. OCLC 2688081 (法語) . ^ Pinkus, Allan; Zafrany, Samy. Fourier Series and Integral Transforms 1st. Cambridge, UK: Cambridge University Press. 1997: 42 –44. ISBN 0-521-59771-4 ^ Katznelson, Yitzhak. An introduction to Harmonic Analysis 2nd corrected. New York, NY: Dover Publications, Inc. 1976: 46. ISBN 0-486-63331-4 ^ Georgi P. Tolstov. Fourier Series . Courier-Dover. 1976. ISBN 0-486-63317-9 ^ 這裡 (頁面存檔備份 ,存於網際網路檔案館 )^ 8.0 8.1 8.2 8.3 8.4 Papula, Lothar. Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler [Mathematical Functions for Engineers and Physicists]. Vieweg+Teubner Verlag. 2009. ISBN 978-3834807571(德語) . ^ 9.0 9.1 9.2 9.3 Shmaliy, Y.S. Continuous-Time Signals. Springer. 2007. ISBN 978-1402062711 ^ Proakis, John G.; Manolakis, Dimitris G. Digital Signal Processing: Principles, Algorithms, and Applications 291 . ISBN 978-0-13-373762-2 ^ Characterizations of a linear subspace associated with Fourier series . MathOverflow. 2010-11-19 [2014-08-08 ] .
延伸閱讀 [ 編輯 ] William E. Boyce; Richard C. DiPrima. Elementary Differential Equations and Boundary Value Problems 8th. New Jersey: John Wiley & Sons, Inc. 2005. ISBN 0-471-43338-1 Joseph Fourier, translated by Alexander Freeman. The Analytical Theory of Heat. Dover Publications. 2003. ISBN 0-486-49531-0 Théorie Analytique de la Chaleur , originally published in 1822.Enrique A. Gonzalez-Velasco. Connections in Mathematical Analysis: The Case of Fourier Series . American Mathematical Monthly. 1992, 99 (5): 427–441. JSTOR 2325087 doi:10.2307/2325087 Fetter, Alexander L.; Walecka, John Dirk. Theoretical Mechanics of Particles and Continua . Courier. 2003. ISBN 978-0-486-43261-8 Felix Klein , Development of mathematics in the 19th century . Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert , Springer, Berlin, 1928.Walter Rudin . Principles of mathematical analysis ISBN 0-07-054235-X A. Zygmund . Trigonometric Series third. Cambridge: Cambridge University Press. 2002. ISBN 0-521-89053-5 電機電子類科《工程數學》,ISBN 978-957-584-377-9 ,作者 陳錫冠、曾致煌,高立出版社。 外部連結 [ 編輯 ] 本條目含有來自PlanetMath 《example of Fourier series 》的內容,版權遵守創用CC協議:署名-相同方式共享 協議 。


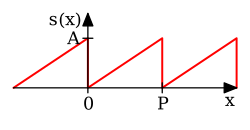






 3rd. Prentice Hall. 1996: 291. ISBN 978-0-13-373762-2.
3rd. Prentice Hall. 1996: 291. ISBN 978-0-13-373762-2.
 3rd. New York: McGraw-Hill, Inc. 1976. ISBN 0-07-054235-X.
3rd. New York: McGraw-Hill, Inc. 1976. ISBN 0-07-054235-X. Hobson, Ernest. Fourier's Series. Encyclopædia Britannica 10 (第11版). London: 753–758. 1911.
Hobson, Ernest. Fourier's Series. Encyclopædia Britannica 10 (第11版). London: 753–758. 1911.

![{\displaystyle [0,P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e22a95e69fea5905acab328644408c110eedea0e)










![{\displaystyle [-P/2,P/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/773e3d42ef176524eeb449749ec2bc0a83b5566a)






































![{\displaystyle [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)






![{\displaystyle [x_{0},\ x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ad7364478493807dcae901dc0091bb7b6ff0fa)




![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
![另一個分別採用傅立葉級數的前 1, 2, 3, 4 項近似方波的可視化。(可以在這裡[7]看到一個交互式的動畫)](http://upload.wikimedia.org/wikipedia/commons/1/1a/Fourier_series_square_wave_circles_animation.gif)

![{\displaystyle {\hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)

![{\displaystyle s(x)=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f87178156b61cc57fc94240bec5985c4ce63d2)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27177d458017a95aa1b728c68060767743e370db)

![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ffcbcac13a0f7db7d5dd8c21183bb89b0d3af9)

















![{\displaystyle x\in [0,P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b67d1c1f507ec8b6185021d3269fc4d4103c57b)
![{\displaystyle R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd850b8b42dd52a3e6a55ac7129524e7d4af105b)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i{\frac {2\pi }{P}}nx_{0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d12b77e7a475835941ca9190940a1c6b11ff848)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)












![{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6f5c4fb95b6f6bb17b2673b083479b652b42e32)
![{\displaystyle {\begin{aligned}s(x)&=A_{0}+\sum _{n=1}^{\infty }\left(A_{n}\cos \left(nx\right)+B_{n}\sin \left(nx\right)\right)\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591d6757bad021d069ecaee42fc178e9830dfbe5)




![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)










![{\displaystyle {\frac {1}{2}}[x(t^{-})+x(t^{+})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49230b01e93db8171d55b34288c6d4d8097278b3)
![{\displaystyle [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)























![{\displaystyle H[n]=(S*R)[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74c5a5260d6ac3aac1292a8e4d4a1b4666082a8b)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c557e56479db0c1f29a2b223cb804b6c0487db)


![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)













![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)


![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)




![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)






