圓內接四邊形

四種圓內接四邊形的例子（四點共圓）

在幾何中，圓內接四邊形（英文：Cyclic quadrilateral）是四邊形的一種。顧名思義，圓內接四邊形的四個頂點都在同一個圓上。

性質

在一個圓內接四邊形中，相對的兩內角是互補的，它們度數之和為180度。與此等價的說法是，圓內接四邊形的一個內角等於其相對面的角的外角。一個四邊形為圓內接四邊形的充分必要條件是其相對的兩內角互補，即，圓內接四邊形相對的兩內角互補，且相對的兩內角互補的四邊形是圓內接四邊形（四邊形四頂點共圓或說有四邊形有外接圓）。

如圖，ABCD為圓內接四邊形，托勒密定理指出：${\begin{matrix}BD\cdot AC\\=AB\cdot CD+BC\cdot DA.\end{matrix}}$

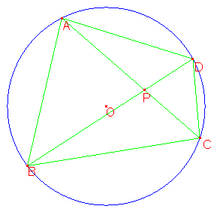
托勒密定理指出，圓內接四邊形的兩組對邊乘積之和等於兩條對角線的乘積（如右圖）。對於非退化的四邊形，如果兩組對邊乘積之和等於兩條對角線的乘積，那麼必定是圓內接四邊形。

凸四邊形的兩條對角線將自身分成四個三角形。如果這個四邊形是圓內接四邊形，那麼相對的兩個三角形是相似的。如右圖中，$P$是圓內接四邊形$ABCD$的兩對角線交點，則$\bigtriangleup ABP\sim \bigtriangleup DCP$，$\bigtriangleup BCP\sim \bigtriangleup ADP$。一個與此等價的說法是所謂的相交弦定理：設凸的圓內接四邊形的兩條對角線相交於一點(圖中的$P$），那麼其中一條對角線被點$P$所分成的兩段的長度之乘積等於另一條對角線被點$P$所分成的兩段的長度之乘積：$AP\times CP=BP\times DP$。相應的逆命題也成立：如果一個四邊形ABCD的兩條對角線交於點$P$，且$\bigtriangleup ABP\sim \bigtriangleup DCP$（或$\bigtriangleup BCP\sim \bigtriangleup ADP$，或$AP\times CP=BP\times DP$），那麼四邊形$ABCD$是圓內接四邊形。

在四邊形中，矩形、正方形都是圓內接四邊形；鳶形和梯形可能是圓內接四邊形。如果一個四邊形既是平行四邊形又是圓內接四邊形，那麼它是一個矩形。如果一個四邊形既是梯形又是圓內接四邊形，那麼它是一個等腰梯形。如果一個鳶形是圓內接四邊形，那麼它至少有一對對角是直角。

面積

在已知四邊的邊長時，圓內接四邊形的面積可通過婆羅摩笈多公式給出。若圓內接四邊形的四邊邊長分別是$a$, $b$, $c$, $d$，則其面積為：

${\sqrt {(p-a)(p-b)(p-c)(p-d)}}$

其中$p$為半周長：

$p={\frac {a+b+c+d}{2}}.$

可以證明，在所有周長為定值$2p$的圓內接四邊形中，面積最大的是正方形。

參見

• 圓內接多邊形
• 婆羅摩笈多公式
• 婆羅摩笈多定理：關於對角線相互垂直的圓內接四邊形的一個定理。
• 外接圓

外部連結

• （英文）體驗圓內接四邊形（頁面存檔備份，存於網際網路檔案館）
• （英文）關於圓內接四邊形的一個定理（頁面存檔備份，存於網際網路檔案館）