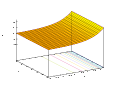
指數函數對於
x
{\displaystyle x}
x
{\displaystyle x}
x
{\displaystyle x}
0
{\displaystyle 0}
1
{\displaystyle 1}
y
{\displaystyle y}
斜率 。 指數函數 (英語:Exponential function )是形式為
b
x
{\displaystyle b^{x}}
函數 ,其中
b
{\displaystyle b}
底數 (或稱基數 ,base ),而
x
{\displaystyle x}
指數 index / exponent )。
現今指數函數 通常特指以
e
{\displaystyle {\mbox{e}}}
e
x
{\displaystyle {\mbox{e}}^{x}}
數學 中重要的函數,也可寫作
exp
(
x
)
{\displaystyle \exp(x)}
e
{\displaystyle {\mbox{e}}}
自然對數函數的底數 ,近似值為
2.718281828
{\displaystyle 2.718281828}
歐拉 數。
作為實數 變量
x
{\displaystyle x}
y
=
e
x
{\displaystyle y={\mbox{e}}^{x}}
圖像 總是正的(在
x
{\displaystyle x}
x
{\displaystyle x}
x
{\displaystyle x}
漸近線 。一般的說,變量
x
{\displaystyle x}
複數 ,甚至是完全不同種類的數學物件 。它的反函數 是定義在所有正數
x
{\displaystyle x}
自然對數
ln
x
{\displaystyle \ln {x}}
本文集中於帶有底數為歐拉數
e
{\displaystyle {\mbox{e}}}
科學 中,術語指數函數 更一般性的用於形如
k
b
x
{\displaystyle kb^{x}}
b
{\displaystyle b}
底數 ,是不等於
1
{\displaystyle 1}
實數 。
最簡單的說,指數函數按恆定速率翻倍。例如細菌培養時細菌總數(近似的)每三個小時翻倍,和汽車的價值每年減少10%都可以被表示為一個指數。特別是複利 ,事實上就是它導致了雅各布·伯努利 在1683年介入了現在叫做
e
{\displaystyle e}
[1]
lim
n
→
∞
(
1
+
1
n
)
n
{\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}
後來約翰·伯努利 在1697年研究了指數函數的微積分。[1]
設1份借貸有
x
{\displaystyle x}
x
12
{\textstyle {\frac {x}{12}}}
(
1
+
x
12
)
{\textstyle (1+{\frac {x}{12}})}
(
1
+
x
12
)
12
{\textstyle (1+{\frac {x}{12}})^{12}}
(
1
+
x
365
)
365
{\textstyle (1+{\frac {x}{365}})^{365}}
[2] 歐拉 提出[3]
exp
(
x
)
=
lim
n
→
∞
(
1
+
x
n
)
n
{\displaystyle \exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}
指數函數有基本的指數恆等式,
exp
(
x
+
y
)
=
exp
(
x
)
⋅
exp
(
y
)
{\displaystyle \exp(x+y)=\exp(x)\cdot \exp(y)}
這是它寫為
e
x
{\displaystyle e^{x}}
[4]
在雅各布·伯努利 之前,約翰·納皮爾 在1614年[5] 約斯特·比爾吉 在6年後[6] 對數表 ,當時通過對接近1的底數的大量乘冪 運算,來找到指定範圍和精度的對數 和所對應的真數,當時還沒出現有理數冪的概念,直到1742年威廉·瓊斯 才發表了現在的冪指數概念[7] 約翰·納皮爾 的底數0.999999910000000 相當接近
1
e
{\textstyle {\frac {1}{e}}}
[8] 約斯特·比爾吉 的底數1.000110000 相當接近自然對數 的底數
e
{\displaystyle e}
約翰·納皮爾 用了20年時間進行相當於數百萬次乘法的計算,亨利·布里格斯 [9] 常用對數 表的編制。
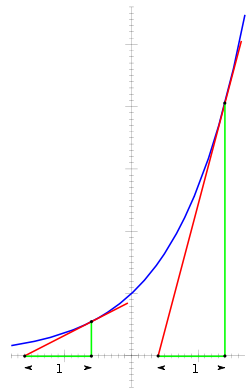
形式定義 [ 編輯 ] 指數函數(藍色),冪級數的前n +1項的和(紅色)。 指數函數
e
x
{\displaystyle e^{x}}
等價 的方式定義。特別是它可以定義為冪級數 :
e
x
=
1
+
∑
n
=
1
∞
x
n
n
!
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
x
4
4
!
+
⋯
{\displaystyle e^{x}=1+\sum _{n=1}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots }
或序列的極限 :
e
x
=
lim
n
→
∞
(
1
+
x
n
)
n
.
{\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{x \over n}\right)^{n}.}
在這些定義中,
n
!
{\displaystyle n!}
n
{\displaystyle n}
階乘 ,而
x
{\displaystyle x}
實數 、複數 、和巴拿赫代數 的元素。
設
x
≥
0
{\displaystyle x\geq 0}
t
n
=
(
1
+
x
n
)
n
,
s
n
=
∑
k
=
0
n
x
k
k
!
.
{\displaystyle t_{n}=\left(1+{\frac {x}{n}}\right)^{n},\ s_{n}=\sum _{k=0}^{n}{\frac {x^{k}}{k!}}.}
據二項式定理 ,
t
n
=
∑
k
=
0
n
(
n
k
)
x
k
n
k
=
1
+
x
+
∑
k
=
2
n
n
(
n
−
1
)
(
n
−
2
)
⋯
[
n
−
(
k
−
1
)
]
x
k
k
!
n
k
=
1
+
x
+
x
2
2
!
(
1
−
1
n
)
+
x
3
3
!
(
1
−
1
n
)
(
1
−
2
n
)
+
⋯
⋯
+
x
n
n
!
(
1
−
1
n
)
⋯
(
1
−
n
−
1
n
)
≤
s
n
{\displaystyle {\begin{aligned}t_{n}&=\sum _{k=0}^{n}{n \choose k}{\frac {x^{k}}{n^{k}}}=1+x+\sum _{k=2}^{n}{\frac {n(n-1)(n-2)\cdots [n-(k-1)]x^{k}}{k!\,n^{k}}}\\[8pt]&=1+x+{\frac {x^{2}}{2!}}\left(1-{\frac {1}{n}}\right)+{\frac {x^{3}}{3!}}\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)+\cdots \\[8pt]&{}\qquad \cdots +{\frac {x^{n}}{n!}}\left(1-{\frac {1}{n}}\right)\cdots \left(1-{\frac {n-1}{n}}\right)\leq s_{n}\end{aligned}}}
(設
x
≥
0
{\displaystyle x\geq 0}
lim sup
n
→
∞
t
n
≤
lim sup
n
→
∞
s
n
=
e
x
{\displaystyle \limsup _{n\to \infty }t_{n}\leq \limsup _{n\to \infty }s_{n}=e^{x}}
可證明當
n
{\displaystyle n}
指數函數的特徵描述
y
=
b
x
{\displaystyle y=b^{x}}
e
{\displaystyle e}
1
2
{\displaystyle {\frac {1}{2}}}
從指數函數的定義:
e
x
=
lim
n
→
∞
(
1
+
x
n
)
n
{\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}
可得出它有冪 運算的「指數定律」:
e
0
=
1
{\displaystyle \!\,e^{0}=1}
e
1
=
e
{\displaystyle \!\,e^{1}=e}
e
x
+
y
=
e
x
e
y
{\displaystyle \!\,e^{x+y}=e^{x}e^{y}}
e
x
y
=
(
e
x
)
y
{\displaystyle \!\,e^{xy}=\left(e^{x}\right)^{y}}
e
−
x
=
1
e
x
{\displaystyle \!\,e^{-x}={1 \over e^{x}}}
它們對所有實數
x
{\displaystyle x}
y
{\displaystyle y}
因為在指數函數的定義中
x
{\displaystyle x}
實數 ,可以使用自然對數 ,把更一般的指數函數,即正實數的實數冪 函數定義為
b
x
=
(
e
ln
b
)
x
=
e
x
ln
b
.
{\displaystyle \!\,b^{x}=(e^{\ln b})^{x}=e^{x\ln b}.}
定義於所有的
b
>
0
{\displaystyle b>0}
實數
x
{\displaystyle x}
b
{\displaystyle b}
乘方 和方根 運算定義的正實數的有理數 冪函數:
b
m
n
=
b
m
n
.
{\displaystyle b^{\frac {m}{n}}={\sqrt[{n}]{b^{m}}}.}
而方根運算可通過自然對數和指數函數來表示(單位根 )
x
n
=
x
1
n
=
e
ln
x
n
.
{\displaystyle {\sqrt[{n}]{x}}=x^{\frac {1}{n}}=e^{\frac {\ln x}{n}}.}
介入數
e
{\displaystyle e}
微積分 中,是通過指數函數和對數 來進行導數 和積分 運算。[10]
y
=
b
x
{\displaystyle y=b^{x}}
極限 形式的導數:
d
d
x
b
x
=
lim
h
→
0
b
x
+
h
−
b
x
h
=
lim
h
→
0
b
x
b
h
−
b
x
h
=
b
x
(
lim
h
→
0
b
h
−
1
h
)
.
{\displaystyle {\frac {d}{dx}}b^{x}=\lim _{h\to 0}{\frac {b^{x+h}-b^{x}}{h}}=\lim _{h\to 0}{\frac {b^{x}b^{h}-b^{x}}{h}}=b^{x}\left(\lim _{h\to 0}{\frac {b^{h}-1}{h}}\right).}
最右端的極限無關於變量
x
{\displaystyle x}
b
{\displaystyle b}
[11] 連鎖法則 :
d
d
x
(
1
+
x
n
)
n
=
(
1
+
x
n
)
n
−
1
.
{\displaystyle {\frac {d}{dx}}\left(1+{\frac {x}{n}}\right)^{n}=\left(1+{\frac {x}{n}}\right)^{n-1}.}
當這個底數是
e
{\displaystyle e}
[4] [12]
d
d
x
e
x
=
e
x
.
{\displaystyle {\frac {d}{dx}}e^{x}=e^{x}.}
導數和微分方程式 [ 編輯 ] 指數函數的導數等於這個函數的值。從在藍色曲線上任意一點
P
{\displaystyle P}
h
{\displaystyle h}
x
{\displaystyle x}
b
{\displaystyle b}
P
{\displaystyle P}
h
{\displaystyle h}
h
{\displaystyle h}
b
{\displaystyle b}
b
{\displaystyle b}
1
{\displaystyle 1}
指數函數在數學和科學中的重要性主要源於它的導數 的性質。特別是
d
d
x
e
x
=
e
x
{\displaystyle {d \over dx}e^{x}=e^{x}}
就是說,
e
x
{\displaystyle e^{x}}
導數 。這可以用泰勒級數 證明:
d
d
x
e
x
=
d
d
x
(
1
+
∑
n
=
1
∞
x
n
n
!
)
=
∑
n
=
1
∞
n
x
n
−
1
n
!
=
∑
n
=
1
∞
x
n
−
1
(
n
−
1
)
!
=
∑
k
=
0
∞
x
k
k
!
,
where
k
=
n
−
1
=
e
x
{\displaystyle {\begin{aligned}{\frac {d}{dx}}e^{x}&={\frac {d}{dx}}\left(1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}\right)=\sum _{n=1}^{\infty }{\frac {nx^{n-1}}{n!}}=\sum _{n=1}^{\infty }{\frac {x^{n-1}}{(n-1)!}}\\[6pt]&=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}},{\text{ where }}k=n-1\\[6pt]&=e^{x}\end{aligned}}}
對於常數
K
{\displaystyle K}
K
e
x
{\displaystyle Ke^{x}}
皮卡-林德洛夫定理 [13]
函數的圖像的在任何一點上的斜率是這個函數在這一點上的高度。
函數在
x
{\displaystyle x}
x
{\displaystyle x}
這個函數是微分方程式
y
′
=
y
{\displaystyle y'=y}
exp是泛函導數 的不動點 。 事實上,很多不同的方程式引發指數函數,包括薛丁格方程式 和拉普拉斯方程式 和簡單諧波運動 的方程式。
對於有其他底數的指數函數:
d
d
x
b
x
=
(
ln
b
)
b
x
{\displaystyle {d \over dx}b^{x}=(\ln b)b^{x}}
所以任何指數函數都是它自己導數的常數 倍。
如果一個變量的增長或衰減速率是與它的大小成比例 的,比如在無限制情況下的人口增長、複利 和放射性衰變 ,則這個變量可以寫為常數倍的時間的指數函數。
進一步的,對任何可微函數
f
(
x
)
{\displaystyle f(x)}
連鎖律 找到:
d
d
x
e
f
(
x
)
=
f
′
(
x
)
e
f
(
x
)
{\displaystyle {d \over dx}e^{f(x)}=f'(x)e^{f(x)}}
e x [ 編輯 ] 通過歐拉連分數公式 得到
e
x
{\displaystyle e^{x}}
連分數 :
e
x
=
1
+
x
1
−
x
x
+
2
−
2
x
x
+
3
−
3
x
x
+
4
−
⋱
{\displaystyle e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}}
e
z
{\displaystyle e^{z}}
廣義連分數 收斂更快速:[14]
e
z
=
1
+
2
z
2
−
z
+
z
2
6
+
z
2
10
+
z
2
14
+
⋱
{\displaystyle e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}}
或者,替換
z
=
x
y
{\displaystyle z={\frac {x}{y}}}
e
x
y
=
1
+
2
x
2
y
−
x
+
x
2
6
y
+
x
2
10
y
+
x
2
14
y
+
⋱
{\displaystyle e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+\ddots }}}}}}}}}
有特殊情況
z
=
2
{\displaystyle z=2}
e
2
=
1
+
4
0
+
2
2
6
+
2
2
10
+
2
2
14
+
⋱
=
7
+
2
5
+
1
7
+
1
9
+
1
11
+
⋱
{\displaystyle e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}}
在複平面上 [ 編輯 ] 指數函數
e
z
{\displaystyle e^{z}}
(
1
+
z
n
)
n
{\displaystyle (1+{\frac {z}{n}})^{n}}
n
{\displaystyle n}
極限 。在本動畫中,
z
=
i
π
3
{\displaystyle z={\frac {i\pi }{3}}}
n
{\displaystyle n}
(
1
+
z
n
)
n
{\displaystyle (1+{\frac {z}{n}})^{n}}
複平面 上
n
{\displaystyle n}
n
{\displaystyle n}
單位圓 ,覆及
π
3
{\displaystyle {\frac {\pi }{3}}}
如同在實數 情況下,在複平面 的指數函數可以用多種等價方式定義。比如冪級數形式的:
e
z
=
∑
n
=
0
∞
z
n
n
!
{\displaystyle e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}}
或者序列的極限 :
e
z
=
lim
n
→
∞
(
1
+
z
n
)
n
{\displaystyle e^{z}=\lim _{n\rightarrow \infty }\left(1+{\frac {z}{n}}\right)^{n}}
它帶有虛數 週期
2
π
i
{\displaystyle 2\pi i}
[prove 1]
e
a
+
b
i
=
e
a
(
cos
b
+
i
sin
b
)
{\displaystyle \!\,e^{a+bi}=e^{a}(\cos b+i\sin b)}
這裡的
a
{\displaystyle a}
b
{\displaystyle b}
歐拉公式 ,這個公式把指數函數和三角函數 與指數函數聯繫起來。
在考慮定義在複平面 上的函數的時候,指數函數擁有重要的性質
e
z
+
w
=
e
z
e
w
{\displaystyle \!\,e^{z+w}=e^{z}e^{w}}
e
0
=
1
{\displaystyle \!\,e^{0}=1}
e
z
≠
0
{\displaystyle \!\,e^{z}\neq 0}
d
d
z
e
z
=
e
z
{\displaystyle \!\,{d \over dz}e^{z}=e^{z}}
(
e
z
)
n
=
e
n
z
,
n
∈
Z
{\displaystyle \,(e^{z})^{n}=e^{nz},n\in \mathbb {Z} }
對於所有的
z
{\displaystyle z}
w
{\displaystyle w}
它是週期的全純函數 。我們看到除了多項式 的所有初等函數 都以某種方式起源於指數函數。
擴展自然對數 到復平面上的多值函數
ln
z
{\displaystyle \ln z}
z
w
=
e
w
ln
z
{\displaystyle \!\,z^{w}=e^{w\ln z}}
對於所有複數
z
{\displaystyle z}
w
{\displaystyle w}
z
{\displaystyle z}
(
e
z
)
w
≠
e
z
w
{\displaystyle (e^{z})^{w}\neq e^{zw}}
(
e
z
)
w
=
e
(
z
+
2
π
i
n
)
w
{\displaystyle (e^{z})^{w}=e^{(z+2\pi in)w}\,}
n 之上。指數函數把在複平面上任何直線 映射到在複平面中以原點 為中心的對數螺線 。要注意兩個特殊情況:當最初的線平行於實數軸的時候,結果的螺線永不遮蓋(close in on)自身;當最初的線平行於虛數軸的時候,結果的螺線是某個半徑的圓。
在複平面上指數函數(主支)
z = Re(e x +iy
z = Im(e x +iy
矩陣和巴拿赫代數 [ 編輯 ] 上面給出的指數函數的定義可以用於所有巴拿赫代數 ,特別是對於方塊矩陣 (在這種情況函數叫做矩陣指數 )。在這種情況下我們有
e
x
+
y
=
e
x
e
y
if
x
y
=
y
x
{\displaystyle \ e^{x+y}=e^{x}e^{y}{\mbox{ if }}xy=yx}
e
0
=
1
{\displaystyle \ e^{0}=1}
e
x
{\displaystyle \ e^{x}}
e
−
x
{\displaystyle \ e^{-x}}
e
x
{\displaystyle \ e^{x}}
x
{\displaystyle \ x}
u
{\displaystyle \ u}
u
e
x
{\displaystyle \ ue^{x}}
在非交換巴拿赫代數的上下文中,比如矩陣代數或在巴拿赫空間 或希爾伯特空間 上的算子,指數函數經常被認做實數參數的函數:
f
(
t
)
=
e
t
A
{\displaystyle \ f(t)=e^{tA}}
這裡的A 是這個代數的固定元素而t 是任何實數。這個函數有重要的性質
f
(
s
+
t
)
=
f
(
s
)
f
(
t
)
{\displaystyle \ f(s+t)=f(s)f(t)}
f
(
0
)
=
1
{\displaystyle \ f(0)=1}
f
′
(
t
)
=
A
f
(
t
)
{\displaystyle \ f'(t)=Af(t)}
在李代數上 [ 編輯 ] 從李代數 到李群 的「指數映射」有著上述性質。事實上因為R 是帶有乘法的所有正實數的李群的李代數,實數參數的常規指數函數是李代數下的特殊情況。類似的,因為所有方塊實數矩陣的李代數M (n , R )屬於所有正可逆方塊矩陣的李群,方塊矩陣的指數函數是李代數指數映射 的特殊情況。
註釋與引用 [ 編輯 ]
^ 1.0 1.1 John J O'Connor; Edmund F Robertson. The number e . School of Mathematics and Statistics. University of St Andrews, Scotland. [2011-06-13 ] . (原始內容存檔 於2015-09-08). ^ 假定利率為100%,借期1年本息合為200%,利息平均每月約8.3%。按複利可以只借1個月,1個月未能還款,本息合計為借款,如此1年下來本息合計約為261.3%。如果借貸者能在1個月內歸還,則不需要付1整年的利息,放貸者快速收回資金可以借給他人;拖到1年歸還,放貸者得到比正常放貸1年要高的利息;1年後按複利計算本息快速增長,借貸者可能就還不起了,而放貸者獲得抵押品。甚至可以逐日借款,這樣1年的收益高於261.3%,但增大不多,而借貸者可以更快還清少付利息,e 就是設立更小還款時限增加獲利,能達到的1年極限收益,即約為 271.8%。應區分抵押貸款 和高利貸 。
^ Eli Maor , e: the Story of a Number , p.156.^ 4.0 4.1
lim
n
→
∞
(
1
+
x
n
)
n
=
lim
n
→
∞
(
(
1
+
1
n
)
n
)
x
{\displaystyle \lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}=\lim _{n\to \infty }\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{x}}
^ Ernest William Hobson, John Napier and the invention of logarithms, 1614 , Cambridge: The University Press, 1914 ^ Boyer, Carl B. , 14, section "Jobst Bürgi" , A History of Mathematics, New York: John Wiley & Sons , 1991, ISBN 978-0-471-54397-8 ^
(
1
+
1
n
)
x
=
(
(
1
+
1
n
)
n
)
x
n
{\displaystyle \left(1+{\frac {1}{n}}\right)^{x}=\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{\frac {x}{n}}}
^ 選取接近e的底數b,對數表涉及的bx 為單調增函數,定義域為0到1而值域為1到b;選取接近1/e的底數b,對數表涉及的bx 為單調減函數,定義域為0到∞而值域為1到0。
^ 以
10
1
2
54
{\displaystyle 10^{\frac {1}{2^{54}}}}
^ Kline, M. (1998) Calculus: An intuitive and physical approach , section 12.3 "The Derived Functions of Logarithmic Functions." (頁面存檔備份 ,存於網際網路檔案館 ), pp. 337 ff, Courier Dover Publications, 1998, ISBN 0-486-40453-6
^
lim
h
→
0
(
b
h
−
1
)
1
h
=
lim
1
n
→
0
(
b
1
n
−
1
)
n
=
lim
n
→
∞
n
(
b
1
/
n
−
1
)
=
ln
(
b
)
.
{\displaystyle {\begin{aligned}\lim _{h\to 0}\left(b^{h}-1\right){\frac {1}{h}}&=\lim _{{\frac {1}{n}}\to 0}\left(b^{\frac {1}{n}}-1\right)n\\&=\lim _{n\rightarrow \infty }n(b^{1/n}-1)\\&=\ln(b).\\\end{aligned}}}
自然對數 定義為歐拉 提出,是他定義的指數函數的逆函數 。
^
d
d
x
(
1
+
x
n
)
n
=
n
n
+
x
(
1
+
x
n
)
n
.
{\displaystyle {\frac {d}{dx}}\left(1+{\frac {x}{n}}\right)^{n}={\frac {n}{n+x}}\left(1+{\frac {x}{n}}\right)^{n}.}
^ 通過
y
(
t
)
=
e
t
,
y
(
0
)
=
K
{\displaystyle y(t)=e^{t},y(0)=K}
f
(
t
,
y
(
t
)
)
=
y
(
t
)
{\displaystyle f(t,y(t))=y(t)}
^ " A.2.2 The exponential function." L. Lorentzen and H. Waadeland, Continued Fractions , Atlantis Studies in Mathematics, page 268. [2014-03-11 ] . (原始內容存檔 於2021-03-08).
外部連結 [ 編輯 ] 

































![{\displaystyle {\begin{aligned}t_{n}&=\sum _{k=0}^{n}{n \choose k}{\frac {x^{k}}{n^{k}}}=1+x+\sum _{k=2}^{n}{\frac {n(n-1)(n-2)\cdots [n-(k-1)]x^{k}}{k!\,n^{k}}}\\[8pt]&=1+x+{\frac {x^{2}}{2!}}\left(1-{\frac {1}{n}}\right)+{\frac {x^{3}}{3!}}\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)+\cdots \\[8pt]&{}\qquad \cdots +{\frac {x^{n}}{n!}}\left(1-{\frac {1}{n}}\right)\cdots \left(1-{\frac {n-1}{n}}\right)\leq s_{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8451a7eb4b301928aa74f4e3565fc942cf9d6c34)











![{\displaystyle b^{\frac {m}{n}}={\sqrt[{n}]{b^{m}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b6ed2731781cb0d0d02467b366f6939c9e7592)
![{\displaystyle {\sqrt[{n}]{x}}=x^{\frac {1}{n}}=e^{\frac {\ln x}{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/291bce0c414e382cbcaaaafce18d5a3726d12099)






![{\displaystyle {\begin{aligned}{\frac {d}{dx}}e^{x}&={\frac {d}{dx}}\left(1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}\right)=\sum _{n=1}^{\infty }{\frac {nx^{n-1}}{n!}}=\sum _{n=1}^{\infty }{\frac {x^{n-1}}{(n-1)!}}\\[6pt]&=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}},{\text{ where }}k=n-1\\[6pt]&=e^{x}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86128e9f129e565851026aed221433047fea96c7)