 使用二次函數擬合一組數據點的結果
使用二次函數擬合一組數據點的結果
最小平方法(英語:least squares method),又稱最小二乘法,是一種數學優化建模方法。它通過最小化誤差的平方和尋找數據的最佳函數匹配。
利用最小平方法可以簡便的求得未知的數據,並使得求得的數據與實際數據之間誤差的平方和為最小。
「最小平方法」是對線性方程組,即方程式個數比未知數更多的方程組,以迴歸分析求得近似解的標準方法。在這整個解決方案中,最小平方法演算為每一方程式的結果中,將殘差平方和的總和最小化。
最重要的應用是在曲線擬合上。最小平方所涵義的最佳擬合,即殘差(殘差為:觀測值與模型提供的擬合值之間的差距)平方總和的最小化。當問題在自變數(x變量)有重大不確定性時,那麼使用簡易迴歸和最小平方法會發生問題;在這種情況下,須另外考慮變量-誤差-擬合模型所需的方法,而不是最小平方法。
最小平方問題分為兩種:線性或普通的最小平方法,和非線性的最小平方法,取決於在所有未知數中的殘差是否為線性。線性的最小平方問題發生在統計迴歸分析中;它有一個封閉形式的解決方案。非線性的問題通常經由疊代細緻化來解決;在每次疊代中,系統由線性近似,因此在這兩種情況下核心演算是相同的。
最小平方法所得出的多項式,即以擬合曲線的函數來描述自變數與預計應變數的變異數關係。
當觀測值來自指數族且滿足輕度條件時,最小平方估計和最大概似估計是相同的。最小平方法也能從動差法得出。
以下討論大多是以線性函數形式來表示,但對於更廣泛的函數族,最小平方法也是有效和實用的。此外,疊代地將局部的二次近似應用於或然性(藉由費雪資訊),最小平方法可用於擬合廣義線性模型。
最小平方法通常歸功於高斯(Carl Friedrich Gauss,1795),但最小平方法是由阿德里安-馬里·勒壤得(Adrien-Marie Legendre)首先發表的。
歷史背景[編輯]
最小平方法發展於天文學和大地測量學領域,科學家和數學家嘗試為大航海探索時期的海洋航行挑戰提供解決方案。準確描述天體的行為是船艦在大海洋上航行的關鍵,水手不能再依靠陸上目標導航作航行。
這個方法是在十八世紀期間一些進步的集大成:
- 不同觀測值的組合是真實值的最佳估計;多次觀測會減少誤差而不是增加,也許在1722年由Roger Cotes首先闡明。
- 在相同條件下採取的不同觀察結果,與只嘗試記錄一次最精確的觀察結果是對立的。這個方法被稱為平均值方法。托馬斯·馬耶爾(Tobias Mayer)在1750年研究月球的天平動時,特別使用這種方法,而拉普拉斯(Pierre-Simon Laplace)在1788年他的工作成果中以此解釋木星和土星的運動差異。
- 在不同條件下進行的不同觀測值組合。該方法被稱為最小絕對偏差法,出現在Roger Joseph Boscovich在1757年他對地球形體的著名作品,而拉普拉斯在1799年也表示了同樣的問題。
- 評定對誤差達到最小的解決方案標準,拉普拉斯指明了誤差的機率密度的數學形式,並定義了誤差最小化的估計方法。為此,拉普拉斯使用了一雙邊對稱的指數分布,現在稱為拉普拉斯分布作為誤差分布的模型,並將絕對偏差之和作為估計誤差。他認為這是他最簡單的假設,他期待得出算術平均值而成為最佳的估計。可相反地,他的估計是後驗中位數。
最小平方法[編輯]
 高斯
高斯
1801年,義大利天文學家朱塞普·皮亞齊發現了第一顆小行星穀神星。經過40天的追蹤觀測後,由於穀神星運行至太陽背後,使得皮亞齊失去了穀神星的位置。隨後全世界的科學家利用皮亞齊的觀測數據開始尋找穀神星,但是根據大多數人計算的結果來尋找穀神星都沒有結果。當年24歲的高斯也計算了穀神星的軌道。奧地利天文學家海因里希·奧伯斯根據高斯計算出來的軌道重新發現了穀神星。
高斯使用的最小平方法的方法發表於1809年他的著作《天體運動論》中,而法國科學家勒壤得於1806年獨立發現「最小平方法」,但因不為世人所知而默默無聞。兩人曾為誰最早創立最小平方法原理發生爭執。
1829年,高斯提供了最小平方法的優化效果強於其他方法的證明,見高斯-馬可夫定理。
 數據點(紅色)、使用最小平方法求得的最佳解(藍色)、誤差(綠色)。
數據點(紅色)、使用最小平方法求得的最佳解(藍色)、誤差(綠色)。
某次實驗得到了四個數據點  :
: 、
、 、
、 、
、 (右圖紅色的點)。我們希望找出一條和這四個點最匹配的直線
(右圖紅色的點)。我們希望找出一條和這四個點最匹配的直線  ,即找出在某種「最佳情況」下能夠大致符合如下超定線性方程組的
,即找出在某種「最佳情況」下能夠大致符合如下超定線性方程組的  和
和  :
:

最小平方法採用的方法是盡量使得等號兩邊差的平方最小,也就是找出這個函數的最小值:
![{\displaystyle {\begin{aligned}S(\beta _{1},\beta _{2})=&\left[6-(\beta _{1}+1\beta _{2})\right]^{2}+\left[5-(\beta _{1}+2\beta _{2})\right]^{2}\\&+\left[7-(\beta _{1}+3\beta _{2})\right]^{2}+\left[10-(\beta _{1}+4\beta _{2})\right]^{2}.\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a54ff2e6eab2c0875cc498b93854f1ad7493ae6)
最小值可以通過對  分別求
分別求  和
和  的偏導數,然後使他們等於零得到。
的偏導數,然後使他們等於零得到。


如此就得到了一個只有兩個未知數的方程組,很容易就可以解出:


也就是說直線  是最佳的。
是最佳的。
人們對由某一變量 或多個變量
或多個變量 ……
…… 構成的相關變量
構成的相關變量 感興趣。如彈簧的形變與所用的力相關,一個企業的盈利與其營業額,投資收益和原始資本有關。為了得到這些變量同
感興趣。如彈簧的形變與所用的力相關,一個企業的盈利與其營業額,投資收益和原始資本有關。為了得到這些變量同 之間的關係,便用不相關變量去構建
之間的關係,便用不相關變量去構建 ,使用如下函數模型
,使用如下函數模型
 ,
,
 個獨立變量或
個獨立變量或 個係數去擬合。
個係數去擬合。
通常人們將一個可能的、對不相關變量t的構成都無困難的函數類型稱作函數模型(如拋物線函數或指數函數)。參數b是為了使所選擇的函數模型同觀測值y相匹配。(如在測量彈簧形變時,必須將所用的力與彈簧的膨脹係數聯繫起來)。其目標是合適地選擇參數,使函數模型最好的擬合觀測值。一般情況下,觀測值遠多於所選擇的參數。
其次的問題是怎樣判斷不同擬合的質量。高斯和勒壤得的方法是,假設測量誤差的平均值為0。令每一個測量誤差對應一個變量並與其它測量誤差不相關(隨機無關)。人們假設,在測量誤差中絕對不含系統誤差,它們應該是純偶然誤差(有固定的變異數),圍繞真值波動。除此之外,測量誤差符合常態分布,這保證了偏差值在最後的結果y上忽略不計。
確定擬合的標準應該被重視,並小心選擇,較大誤差的測量值應被賦予較小的權。並建立如下規則:被選擇的參數,應該使算出的函數曲線與觀測值之差的平方和最小。用函數表示為:

用歐幾里得度量表達為:

又因為 ≥0,
≥0,
所以也可以表示為
最小化問題的精度,依賴於所選擇的函數模型。
線性函數模型[編輯]
典型的一類函數模型是線性函數模型。最簡單的線性式是 ,寫成矩陣式,為
,寫成矩陣式,為

直接給出該式的參數解:
 和
和 
其中 ,為t值的算術平均值。也可解得如下形式:
,為t值的算術平均值。也可解得如下形式:

簡單線性模型 y = b0 + b1t 的例子[編輯]
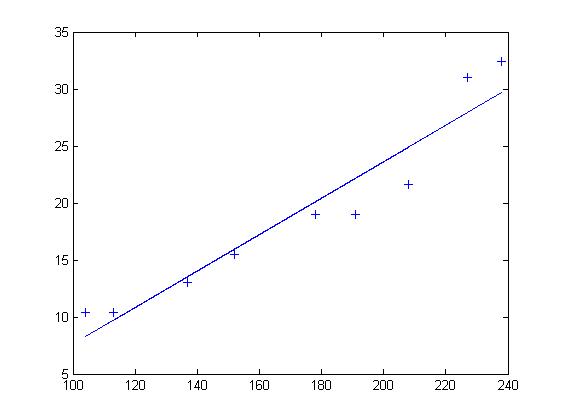
隨機選定10艘戰艦,並分析它們的長度與寬度,尋找它們長度與寬度之間的關係。由下面的描點圖可以直觀地看出,一艘戰艦的長度(t)與寬度(y)基本呈線性關係。散點圖如下:

以下圖表列出了各戰艦的數據,隨後步驟是採用最小平方法確定兩變量間的線性關係。
| 編號
|
長度 (m)
|
寬度 (m)
|
ti - t
|
yi - y
|
|
|
|
| i
|
ti
|
yi
|
ti*
|
yi*
|
ti*yi*
|
ti*ti*
|
yi*yi*
|
| 1
|
208
|
21.6
|
40.2
|
3.19
|
128.238
|
1616.04
|
10.1761
|
| 2
|
152
|
15.5
|
-15.8
|
-2.91
|
45.978
|
249.64
|
8.4681
|
| 3
|
113
|
10.4
|
-54.8
|
-8.01
|
438.948
|
3003.04
|
64.1601
|
| 4
|
227
|
31.0
|
59.2
|
12.59
|
745.328
|
3504.64
|
158.5081
|
| 5
|
137
|
13.0
|
-30.8
|
-5.41
|
166.628
|
948.64
|
29.2681
|
| 6
|
238
|
32.4
|
70.2
|
13.99
|
982.098
|
4928.04
|
195.7201
|
| 7
|
178
|
19.0
|
10.2
|
0.59
|
6.018
|
104.04
|
0.3481
|
| 8
|
104
|
10.4
|
-63.8
|
-8.01
|
511.038
|
4070.44
|
64.1601
|
| 9
|
191
|
19.0
|
23.2
|
0.59
|
13.688
|
538.24
|
0.3481
|
| 10
|
130
|
11.8
|
-37.8
|
-6.61
|
249.858
|
1428.84
|
43.6921
|
| 總和(Σ)
|
1678
|
184.1
|
0.0
|
0.00
|
3287.820
|
20391.60
|
574.8490
|
仿照上面給出的例子
 並得到相應的
並得到相應的 .
.
然後確定b1


可以看出,戰艦的長度每變化1m,相對應的寬度便要變化16cm。並由下式得到常數項b0:

在這裡隨機理論不加闡述。可以看出點的擬合非常好,長度和寬度的相關性大約為96.03%。
利用Matlab得到擬合直線:
一般線性情況[編輯]
若含有更多不相關模型變量 ,可如組成線性函數的形式
,可如組成線性函數的形式

即線性方程組

通常人們將tij記作數據矩陣 A,參數bj記做參數向量b,觀測值yi記作Y,則線性方程組又可寫成:
 即
即 
上述方程式運用最小平方法導出為線性平變異數計算的形式為:
 。
。
最小平方法的解[編輯]

的特解為A的廣義逆矩陣與Y的乘積,這同時也是二範數極小的解,其通解為特解加上A的零空間。證明如下:
先將Y拆成A的值域及其正交補餘兩部分



所以 ,可得
,可得

故若且唯若 是
是 解時,
解時, 即為最小平方解,即
即為最小平方解,即 。
。
又因為

故 的通解為
的通解為

因為

所以 又是二範數極小的最小平方解。
又是二範數極小的最小平方解。
參考文獻[編輯]
外部連結[編輯]
















![{\displaystyle {\begin{aligned}S(\beta _{1},\beta _{2})=&\left[6-(\beta _{1}+1\beta _{2})\right]^{2}+\left[5-(\beta _{1}+2\beta _{2})\right]^{2}\\&+\left[7-(\beta _{1}+3\beta _{2})\right]^{2}+\left[10-(\beta _{1}+4\beta _{2})\right]^{2}.\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a54ff2e6eab2c0875cc498b93854f1ad7493ae6)














































