正交振幅調變
 | |||||||||||||||
| 調變方式 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 連續調變 | |||||||||||||||
| |||||||||||||||
| 脈衝調變 | |||||||||||||||
| 類比 | PAM · PDM · PPM | ||||||||||||||
| 數位 | PCM · PWM | ||||||||||||||
| 展頻 | |||||||||||||||
| CSS · DSSS · THSS · FHSS | |||||||||||||||
| 另見 | |||||||||||||||
| 調變 · 線路碼 · 數據機 · ΔΣ調變 · OFDM · FDM | |||||||||||||||

正交振幅調變(QAM,Quadrature Amplitude Modulation)是一種在兩個正交載波上進行振幅調變的調變方式。這兩個載波通常是相位差為90度(π/2)的正弦波,因此被稱作正交載波。這種調變方式因此而得名。
概述[編輯]
同其它調變方式類似,QAM通過載波某些參數的變化傳輸資訊。在QAM中,數據訊號由相互正交的兩個載波的振幅變化表示。
類比訊號的相位調變和數位訊號的PSK可以被認為是振幅不變、僅有相位變化的特殊的正交振幅調變。由此,類比訊號頻率調變和數位訊號FSK也可以被認為是相位調變(PSK)的特例,因為它們本質上就是相位調變。這裡主要討論數位訊號的QAM,雖然類比訊號QAM也有很多應用,例如NTSC和PAL制式的電視系統就利用正交的載波傳輸不同的顏色分量。
類似於其他數位調變方式,QAM發射訊號集可以用星座圖方便地表示。星座圖上每一個星座點對應發射訊號集中的一個訊號。設正交振幅調變的發射訊號集大小為,稱之為N-QAM。星座點經常採用水平和垂直方向等間距的正方網格配置,當然也有其他的配置方式。數位通訊中數據常採用二進位表示,這種情況下星座點的個數一般是2的冪。常見的QAM形式有16-QAM、64-QAM、256-QAM,以及未來5G採用之512-QAM及1024-QAM。星座點數越多,每個符號能傳輸的資訊量就越大。但是,如果在星座圖的平均能量保持不變的情況下增加星座點,會使星座點之間的距離變小,進而導致誤位元速率上升。因此高階星座圖的可靠性比低階要差。
當對數據傳輸速率的要求高過8-PSK能提供的上限時,一般採用QAM的調變方式。因為QAM的星座點比PSK的星座點更分散,星座點之間的距離因之更大,所以能提供更好的傳輸性能。但是QAM星座點的振幅不是完全相同的,所以它的解調器需要能同時正確檢測相位和振幅,不像PSK解調只需要檢測相位,這增加了QAM解調器的複雜性。
M-QAM訊號波形的表達式為:
- 其中為碼元訊號脈波。
因此QAM可以分解為分別在兩個正交的載波與上的M1-PAM與M2-PAM的疊加,其中。
將上面變形得到
- 其中,。
因此,M-QAM還可以看作是M1-PAM與M2-PSK的疊加,其中。
效能[編輯]
數位通訊中經常用錯誤率(包括誤符號率和誤位元率)與訊號雜訊比的關係衡量調變和解調方式的性能。下面給出一些概念的記法,以得到AWGN頻道下錯誤率的表達式:
- 表示有著零均值和單位方差的高斯隨機變數t 大於x的機率。它與高斯誤差補函數的關係是:。
矩形QAM[編輯]
矩形QAM(Rectangular QAM)的星座圖呈矩形網格配置。因為矩形QAM訊號之間的最小距離並不是相同能量下最大的,因此它的誤位元速率性能沒有達到最優。不過,考慮到矩形QAM等效於兩個正交載波上的脈波振幅調變(PAM)的疊加,因此矩形QAM的調變解調比較簡單。而後面介紹的非矩形QAM雖然能達到略好一些的誤位元速率性能,但是付出的代價是困難得多的調變和解調。
最早的矩形QAM一般是16-QAM。其原因是很容易就看得出來2-QAM和4-QAM實際上是二進位相移鍵控(BPSK)和正交相移鍵控(QPSK),而8-QAM則有將單數位的位分到兩個載波上的問題,8-PSK要容易得多,因此8-QAM很少被使用。
誤位元速率性能[編輯]
- 對於偶數- QAM的誤位元速率性能
可以通過單個正交載波上PAM的性能近似得到QAM的誤位元速率。假設矩形-QAM可分解為兩個正交的-PAM,則有
- ,
因此
- .
精確的誤位元率要看位元與碼元符號之間的映射關係。對於以格雷碼作bit配置並且每個載波承載相同位元數的情況,由於相鄰兩個符號之間僅相差一個位元,因此可以得到誤位元率:
- ,
由於子載波相互獨立,所以:
- 對於奇數- QAM的誤位元速率性能
對於如8-QAM()要給出誤位元速率要困難得多,一個近似上限為:
- .
精確的誤位元率要看位的排列。
非矩形QAM[編輯]
QAM本身有許多可以使用的排列,這裡只列出兩種為例。
環狀8-QAM是最佳的8-QAM,它可以使用最低的平均能量來達到最小的歐幾里得度量。環狀的16-QAM是亞優化的。環狀的QAM非常好地顯示出QAM與PSK之間的關係。不規則QAM的錯誤率很難廣泛地給出,因為它們按其排列各不相同。顯然的上限是歐幾里得度量:
- .
在這裡誤位元速率也與位的排列有關。
雖然對一個特別的有最佳的、不規則的QAM,但是一般人們還是使用規則的QAM,因為它們的調變和解調要方便得多。
星座圖表示[編輯]
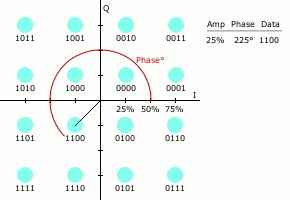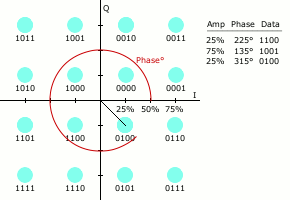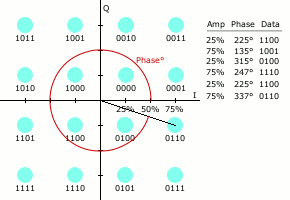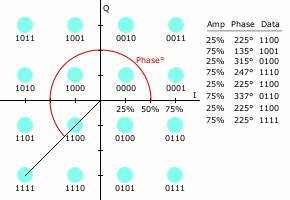
類似於其他數位調變方式,QAM發射的訊號集可以用星座圖方便地表示,星座圖上每一個星座點對應發射訊號集中的那一點。
星座的配置方式。
數位通訊中數據常採用二進位數表示,這種情況下星座點的個數一般是2的冪。
星座點數越多,每個符號能傳輸的資訊量就越大。但是,如果在星座圖的平均能量保持不變的情況下增加星座點,會使星座點之間的距離變小,進而導致誤位元速率上升。因此高階星座圖的可靠性比低階要差。
採用QAM調變技術,頻道帶寬至少要等於碼元速率,為了定時恢復,還需要另外的帶寬,一般要增加15%左右。
優缺點[編輯]
與其他調變技術相比,QAM編碼具有能充分利用帶寬、抗雜訊能力強等優點。
但QAM調變技術用於ADSL的主要問題是如何適應不同電話線路之間較大的性能差異。要取得較為理想的工作特性,QAM接收器需要一個和發送端具有相同的頻譜和相應特性的輸入訊號用於解碼,QAM接收器利用自適應均衡器來補償傳輸過程中訊號產生的失真,因此採用QAM的 ADSL系統的複雜性來自於它的自適應均衡器。
當對數據傳輸速率的要求高過8-PSK能提供的上限時,一般採用QAM的調變方式。因為QAM的星座點比PSK的星座點更分散,星座點之間的距離因此更大,所以能提供更好的傳輸性能。
但是QAM星座點的振幅不是完全相同的,所以它的解調器需要能同時正確檢測相位和振幅,不像PSK解調只需要檢測相位,這增加了QAM解調器的複雜性。


![{\displaystyle s_{m}(t)=\Re [(A_{mc}+jA_{ms})g(t)e^{j2\pi f_{c}t}]=A_{mc}g(t)\cos 2\pi f_{c}t-A_{ms}g(t)\sin 2\pi f_{c}t{\mbox{ ,where }}m=1,2,\ldots ,M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d19aba03080c3cb4ddee9b49bdafe93f2d8a1fbc)





![{\displaystyle s_{m}(t)=\Re [V_{m}e^{j\theta m}g(t)e^{j2\pi f_{c}t}]=V_{m}g(t)\cos(2\pi f_{c}t+\theta _{m})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba86369fc7f0031d73933c01a842fb26ab1a7038)






















