熱力學第二定律
| 熱力學 |
|---|
 |
熱力學第二定律(英語:second law of thermodynamics)是熱力學的四條基本定律之一,表述熱力學過程的不可逆性——孤立系統自發地朝著熱力學平衡方向──最大熵狀態──演化,同樣地,第二類永動機永不可能實現。
這一定律的歷史可追溯至尼古拉·卡諾對於熱機效率的研究,及其於1824年提出的卡諾定理[1]:176-177。定律有許多種表述,其中最具代表性的是克勞修斯表述(1850年)和克耳文表述(1851年),這些表述都可被證明是等價的。定律的數學表述主要藉助克勞修斯所引入的熵的概念,具體表述為克勞修斯定理。
雖然這一定律在熱力學範疇內是一條經驗定律,最初無法得到解釋,但隨著統計力學的發展,這一定律逐漸得到解釋[2]:288-292。
這一定律本身及所引入的熵的概念對於物理學及其他科學領域有深遠意義。定律本身可作為過程不可逆性[2]:262及時間流向的準則。而路德維希·波茲曼對於熵的微觀解釋——系統微觀粒子無序程度的量度,更使這概念被引用到物理學之外諸多領域,如資訊理論及生態學等[2]:287。
定律的自然語言表述[編輯]
克勞修斯表述[編輯]

克勞修斯表述是以熱量傳遞的不可逆性(即熱量總是自發地從高溫熱源流向低溫熱源)作為出發點。
雖然可以藉助冰箱使熱量從低溫熱源流向高溫熱源,但這過程是藉助外界對製冷機做功實現的,即這過程除了有熱量的傳遞,還有功轉化為熱的其他影響。
1850年克勞修斯將這一規律總結為:
| “ | 不可能把熱量從低溫物體傳遞到高溫物體而不產生其他影響。[3] | ” |
克耳文表述[編輯]

克耳文表述是以第二類永動機不可能實現這一規律作為出發點。
第二類永動機是指可以將從單一熱源吸熱全部轉化為功,但大量事實證明這個過程是不可能實現的。功能夠自發地、無條件地全部轉化為熱;但熱轉化為功是有條件的,而且轉化效率有所限制。也就是說功自發轉化為熱這一過程只能單向進行而不可逆。
1851年克耳文勳爵把這一普遍規律總結為:
| “ | 不可能從單一熱源吸收能量,使之完全變為有用功而不產生其他影響。 | ” |
兩種表述的等價性[編輯]
上述兩種表述可以論證是等價的:
- 如果克耳文表述不真,那麼克勞修斯表述不真:假設存在違反克耳文表述的熱機A,可以從低溫熱源吸收熱量並將其全部轉化為有用功。假設存在熱機B,可以把功完全轉化為熱量並傳遞給高溫熱源(這在現實中可實現)。此時若讓A、B聯合工作,則可以看到從低溫熱源流向高溫熱源,而並未產生任何其他影響,即克勞修斯表述不真。
- 如果克勞修斯表述不真,那麼克耳文表述不真:假設存在違反克勞修斯表述的製冷機A,可以在不利用外界對其作的功的情況下,使熱量由低溫熱源流向高溫熱源。假設存在熱機B,可以從高溫熱源吸收熱量並將其中的熱量轉化為有用功,同時將熱量傳遞給低溫熱源(這在現實中可實現)。此時若讓A、B聯合工作,則可以看到A與B聯合組成的熱機從高溫熱源吸收熱量並將其完全轉化為有用功,而並未產生任何其他影響,即克耳文表述不真。
從上述二點,可以看出上述兩種表述是等價的。[2]:259-260
卡拉西奧多里原理[編輯]

卡拉西奧多里原理是康斯坦丁·卡拉西奧多里在1909年給出的公理性表述:
| “ | 在一個系統的任意給定平衡態附近,總有這樣的態存在:從給定的態出發,不可能經過絕熱過程得到。 | ” |
值得注意的是,卡拉西奧多里原理如果要和克耳文表述及克勞修斯表述等價,需要輔以普朗克原理(起始處於內部熱平衡的封閉系統,等體積功總會增加其內能)。[4][5][6][7]
定律的其他表述[編輯]
除上述幾種表述外,熱力學第二定律還有其他表述。 如針對焦耳熱功當量實驗的普朗克表述[2]:259-260:
| “ | 不可存在一個機器,在循環動作中把一重物升高而同時使一熱庫冷卻。 | ” |
以及較為近期的黑首保勞-肯南表述(Hatsopoulos-Keenan statement)[8]:
| “ | 對於一個有給定能量,物質組成,參數的系統,存在這樣一個穩定的平衡態:其他狀態總可以通過可逆過程達到之。 | ” |
可以論證,這些表述與克勞修斯表述以及克耳文表述是等價的[9]。
定律的推論[編輯]
卡諾定理[編輯]

卡諾定理是尼古拉·卡諾於1824年在《談談火的動力和能發動這種動力的機器》中發表的有關熱機效率的定理。值得注意的是定理是在熱力學第二定律提出20餘年前已然提出,從歷史角度來說其為熱力學第二定律的理論來源。但是卡諾本人給出的證明是在熱質說的錯誤前提下進行的證明[1]:176[2]:265,而對於其相對嚴密(以熱動說為前提,而非熱質說)的證明需要熱力學第二定律。
定理的表述[編輯]
卡諾定理表述為:
| “ | 1. 在相同的高溫熱源和低溫熱源間工作的一切可逆熱機的效率都相等。
2. 在相同的高溫熱源和低溫熱源間工作的一切熱機中,不可逆熱機的效率不可能大於可逆熱機的效率。 |
” |
卡諾循環[編輯]
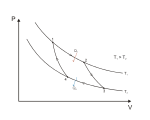
在定理表述中的可逆熱機工作機制是按照卡諾於1824年所提出的卡諾循環,是由兩個絕熱過程,兩個等溫過程組成的循環。利用熱力學第一定律和理想氣體狀態方程式,可以得到其效率。(其中、為熱力學溫標下高、低溫熱源溫度)
卡諾定理的證明[編輯]

定理可以利用熱力學第二定律的克勞修斯表述進行證明。[2]:266-267
假設存在一違反卡諾定理的不可逆機(圖中左邊的熱機),其效率大於在相同熱源和()間工作的可逆機效率。此時可見,當其從吸收熱量時,其輸出有用功,同時向釋放熱量。
當可逆機(圖中右邊的卡諾熱機)輸出同樣多有用功時,其從吸收熱量,向釋放熱量。
此時使可逆機逆向運轉(即作為製冷機)並與不可逆機聯合工作,不難看出有熱量從流向而未產生其他影響,違反克勞修斯表述。則這種不可逆機不可能存在,定理得證。
熱力學溫標[編輯]
熱力學溫標是由克耳文勳爵於1848年利用卡諾定理引入的。它是一個相當理想的溫標,因為它與測溫物質屬性無關。
其可以通過下列過程引入[1]:173-176:
由卡諾定理,可逆機效率只與熱源的溫度有關,而與工作物質無關。考察熱機效率的定義(其中為熱機對外作功,為熱機從高溫熱源吸熱,為熱機向低溫熱源放熱)。則可定義一個關於某溫標下兩熱源溫度、函數。
經過簡單推導,可以證明,對於任意三個溫度、、,存在。易見(其中為形式可選擇的普適函數),不妨令,則可得出。
這樣取定的溫標,由於卡諾定理,是與測溫物質無關的,即熱力學溫標(開氏溫標)。
由於定義式只給出了兩個溫度的比值,仍需要一個標準點:取水的三相點,為273.16K。(1954年國際計量大會決定)
克勞修斯定理[編輯]

克勞修斯定理,又稱「克勞修斯不等式」,是克勞修斯於1862年提出以說明系統流入的熱量與其熵以及周圍環境的關係。這一定理提供了熱力學第二定律的數學表述。 定理可由下列過程得到:
- 考察可逆循環的效率,不難得出其總吸熱、總放熱與熱源溫度、()存在。由於、以及、分別對應循環的兩個等溫過程,而在絕熱過程中,。可以得到在這個循化過程中[2]:271-272。
- 對於不可逆循環,對循環過程進行微分,與在相同熱源的可逆循環進行比較,利用卡諾定理,得到。[10]
綜上,可以得到對於一切在給定熱源下的工作循環,系統流入的熱量與環境溫度T存在:。若且唯若工作循環為可逆循環時[11]。
熵[編輯]
熵的熱力學定義[編輯]
熵作為狀態參量最早由克勞修斯於1854年首次引入,1865年他把這一狀態參量命名為Entropie(德語)(來源於希臘語τρoπή, umkehren,轉變)。[1]:184[2]:274
其引入過程如下:
考察可逆循環過程中的克勞修斯不等式,可以得到循環中某一過程L(始、末狀態分別為a、b)中,只與a,b有關,而與具體路徑無關。
則必然存在一態函數:其微分量為,定義這個函數為熵()。
則對於可逆過程L, ,而不可逆過程的熵變可以通過相應的可逆過程求得 。
熵增加原理[編輯]
考察一系列不可逆過程中熵的變化(如在絕熱環境中理想氣體的真空自由膨脹,在絕熱環境中兩物體間熱傳遞等等)經過計算,可以得到,這些過程中系統的熵。
而現在已有大量的實驗證明:
| “ | 熱力學系統從一個平衡態到另一平衡態的過程中,其熵永不減少:若過程可逆,則熵不變;若不可逆,則熵增加。 | ” |
即熵增加原理。
通過熵增加原理,可以得到對於一個孤立系統,其內部自發進行的與熱相關的過程必然向熵增的方向進行。而孤立系統不受外界任何影響,且系統最終處於平衡態,則在平衡態時,系統的熵取最大值。由此,熵增加原理則可作為不可逆過程準則。可以證明熵增加原理與克勞修斯表述及克耳文表述等價。[2]:280-284
波茲曼關係[編輯]

波茲曼關係是對熵的微觀(統計意義的)解釋,表述為:系統的熵與其微觀狀態數存在函數關係,其中為波茲曼常數。其可通過熱力學第一定律,熵的熱力學定義,及馬克士威-波茲曼統計推出。值得注意的是這一關係在波茲曼生前並未具體給出,僅在1872年時說明與有正比關係。這一公式首次具體給出是在馬克斯·普朗克的《熱輻射》講義中。[2]:286
波茲曼關係給出了熵的微觀解釋——系統微觀粒子的無序程度的度量,並對熵這一概念引入資訊理論、生態學等其他領域具有深遠意義。
定律的解釋[編輯]
由於熱力學自身局限性(它僅適用於粒子很多的宏觀系統,它把物質視作「連續體」,不考慮物質的微觀結構。)[2]:3,因而在熱力學自身範疇內,定律只能作為經驗定律而不能得到解釋。如果要對定律進行解釋,需要藉助統計力學的方法。引用熵的統計力學解釋(波茲曼關係)結合熱力學定律,可以對較為典型的不可逆熱力學過程進行分析,從而得出對熱力學第二定律的解釋[2]:288-292:
| “ | 孤立系統的自發過程總是從熱力學機率小的宏觀狀態向熱力學機率大的宏觀狀態轉變 | ” |
與熱力學其他定律的聯繫[編輯]
與熱力學第一定律的聯繫[編輯]
熱力學第一定律主要從數量上說明功和熱量對系統內能改變在數量上的等價性。熱力學第二定律揭示了熱量與功的轉化,及熱量傳遞的不可逆性。兩者對於全面的描述一個熱力學過程都是不可或缺的。[2]:263-264
與熱力學第零定律的聯繫[編輯]
熱力學第零定律是在兩物體處於熱平衡前提下判定溫度,在未達熱平衡時不適用。在未達熱平衡時可利用熱力學第二定律,通過判定熱傳遞方向來判定兩物體的溫度。[2]:263-264
對定律的詰難[編輯]
馬克士威妖[編輯]
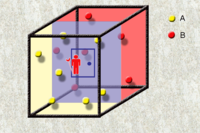

馬克士威妖是詹姆斯·馬克士威假想存在的一理想模型。馬克士威設想了一個容器被分為裝有相同溫度的同種氣體的兩部分A、B。馬克士威妖看守兩部分間「暗門」,可以觀察分子運動速度,並使分子運動較快的分子向確定的一部分流動,而較慢的分子向另一部分流動。經過充分長的時間,兩部分分子運動的平均速度即溫度(參考統計力學中對於溫度的微觀解釋)產生差值並越來越大。經過運算可以得到這一過程是熵減過程,而馬克士威妖的存在使這一過程成為自發過程,這是明顯有悖於熱力學第二定律的。
對其最為有名的回應之一是由利奧·西拉德於1929年提出。西拉德指出如果馬克士威妖真正存在,那麼它觀察分子速度及獲取資訊的過程必然產生額外的能量消耗, 產生熵。[1]:198
洛施密特悖論[編輯]

洛施密特悖論,又稱可反演性悖論,指出如果對符合具有時間反演性的動力學規律的微觀粒子進行反演,那麼系統將產生熵減的結果,這是明顯有悖於熵增加原理的。
針對這一悖論,波茲曼提出:熵增過程確實並非一個單調過程,但對於一個宏觀系統,熵增出現要比熵減出現的機率要大得多;即使達到熱平衡,熵也會圍繞著其最大值出現一定的漲落,且幅度越大的漲落出現機率越小。[1]:196[12]現在已有的一些實驗結果與波茲曼的敘述基本相符。
吉布斯悖論[編輯]

波茲曼關係給出了一個並不外延的熵的表示方法。這導致產生了一個明顯有悖於熱力學第二定律的結論,吉布斯悖論——其允許一個封閉系統的熵減少。在通常的解釋中,都會引用量子力學中粒子的不可區分性去說明系統中粒子本身性質並不影響系統的熵來避免產生這一悖論。然而現在有越來越多論文採用如是觀點:熵闡釋的改變恰恰可以忽略由於分子本身排列方式改變所帶來的影響。而現有的Sackur-Tetrode方程式對於理想氣體的熵的解釋是外延的。[12]
龐加萊始態復現[編輯]
1892年,昂利·龐加萊證明了這樣一個定理:
| “ | 孤立的,有限的保守動力學系統的組態在足夠長久時間後可回復到任意接近初始組態。 | ” |
即龐加萊復現定理。
1896年,恩斯特·策梅洛引用這一定理對於熱力學第二定律進行詰難,認為熱力學與動力學不兼容,並似乎得到了普朗克以及龐加萊本人的支持。[1]:197針對這一觀點,波茲曼引用漲落的概念調和熱力學與動力學,認為復現是依靠漲落實現的。據他估計對一個有個(標準情況下,約0.037ml的氣體所包含的氣體粒子數)粒子的系統,復現時間的數量級為(易見這個數字過分龐大,以致對於時間單位選取是無意義的)[1]:197。而宇宙的年齡約為秒,因而可見,龐加萊始態復現定理對於一個宏觀熱力學系統是沒有現實意義的。
熱寂說[編輯]
如果將熱力學第一、第二定律運用於宇宙,這一典型的孤立系統,將得到這樣的結論:1.宇宙能量守恆,2.宇宙的熵不會減少。那麼將得到,宇宙的熵終將達到極大值,即宇宙將最終達到熱平衡,稱熱寂。
在十九世紀,對於熱寂說有兩個較為有影響的駁斥,一個是由波茲曼提出的「漲落說」(1872)[12],另一個是恩格斯利用運動不滅在《自然辯證法》中進行的駁斥(1876)。現今對於宇宙的理解(1. 宇宙在膨脹;2. 宇宙,作為自重力系統,是具有負熱容的不穩定系統)指出宇宙是不穩定的熱力學系統,並不像靜態宇宙模型所設想的那樣具有平衡態,因而其熵亦無最大值,即熱寂並不存在。[13]
參閱[編輯]
參考文獻[編輯]
- ^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 趙凱華; 羅蔚因. 《新概念物理教程 热学》第二版. 高等教育出版社. ISBN 9787040066777.
- ^ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 秦允豪. 《普通物理学教程 热学》第三版. 高等教育出版社. 2011. ISBN 978-7-04-030090-1.
- ^ Clausius, R. The Mechanical Theory of Heat – with its Applications to the Steam Engine and to Physical Properties of Bodies. London: John van Voorst. 1867 [19 June 2012].
- ^ Planck, M. (1926). Über die Begründing des zweiten Hauptsatzes der Thermodynamik, S.B. Preuß. Akad. Wiss. phys. math. Kl.: 453–463.
- ^ Buchdahl, H.A. (1966). The Concepts of Classical Mechanics, Cambridge University Press, Cambridge UK, p. 69.
- ^ Münster, A. (1970). Classical Thermodynamics, Wiley—Interscience, London, ISBN 978-0-471-62430-1, p. 45.
- ^ Lieb, E.H., Yngvason, J. (1999). The physics and mathematics of the second law of thermodynamics, Phys. Rep., 310: 1–96, p. 49.
- ^ Principles of General Thermodynamics. Krieger, 1981.
- ^ Gyftopoulos, E. P., Beretta, G. P. Thermodynamics: Foundations and Applications. Dover Publications, 2005.
- ^ 范康年. 《物理化学》第二版. 高等教育出版社. 2005: 460. ISBN 7-04-016767-0.
- ^ Clausius theorem (頁面存檔備份,存於網際網路檔案館) at Wolfram Research
- ^ 12.0 12.1 12.2 Von dem c. M. Ludwig Boltzmann in Graz Sitzb. d. Kaiserlichen Akademie der Wissenschaften,mathematich-naturwissen Cl. LXXVI, Abt II, 1877, pp. 373-435.
- ^ 趙凱華. 《定性与半定量物理学》第二版. 高等教育出版社. 2008: 236 - 237. ISBN 978-7-04-022522-8.
擴展閱讀[編輯]
- Goldstein, Martin, and Inge F., 1993. The Refrigerator and the Universe. Harvard Univ. Press. Chpts. 4–9 contain an introduction to the Second Law, one a bit less technical than this entry. ISBN 978-0-674-75324-2
- Leff Harvey S., and Rex, Andrew F. (eds.) 2003. Maxwell's Demon 2 : Entropy, classical and quantum information, computing. Bristol UK; Philadelphia PA: Institute of Physics. ISBN 978-0-585-49237-7
- Halliwell, J.J. Physical Origins of Time Asymmetry. Cambridge. 1994. ISBN 978-0-521-56837-1.(technical).
- Carnot, Sadi. Thurston, Robert Henry , 編. Reflections on the Motive Power of Heat and on Machines Fitted to Develop That Power. New York: J. Wiley & Sons. 1890. (full text of 1897 ed. (頁面存檔備份,存於網際網路檔案館)) (html (頁面存檔備份,存於網際網路檔案館))
- Stephen Jay Kline (1999). The Low-Down on Entropy and Interpretive Thermodynamics, La Canada, CA: DCW Industries. ISBN 1-928729-01-0.
- Kostic, M. Revisiting The Second Law of Energy Degradation and Entropy Generation: From Sadi Carnot's Ingenious Reasoning to Holistic Generalization. AIP Conference Proceedings 1411. 2011: 327–350. Bibcode:2011AIPC.1411..327K. CiteSeerX 10.1.1.405.1945
 . ISBN 978-0-7354-0985-9. doi:10.1063/1.3665247.
. ISBN 978-0-7354-0985-9. doi:10.1063/1.3665247. |journal=被忽略 (幫助);|issue=被忽略 (幫助) also at [1].
外部連結[編輯]
- Stanford Encyclopedia of Philosophy: "Philosophy of Statistical Mechanics (頁面存檔備份,存於網際網路檔案館)" – by Lawrence Sklar.
- Second law of thermodynamics (頁面存檔備份,存於網際網路檔案館) in the MIT Course Unified Thermodynamics and Propulsion (頁面存檔備份,存於網際網路檔案館) from Prof. Z. S. Spakovszky
- E.T. Jaynes, 1988, "The evolution of Carnot's principle (頁面存檔備份,存於網際網路檔案館)," in G. J. Erickson and C. R. Smith (eds.)Maximum-Entropy and Bayesian Methods in Science and Engineering, Vol 1: p. 267.
- Caratheodory, C., "Examination of the foundations of thermodynamics," trans. by D. H. Delphenich (頁面存檔備份,存於網際網路檔案館)
- The Second Law of Thermodynamics (頁面存檔備份,存於網際網路檔案館), BBC Radio 4 discussion with John Gribbin, Peter Atkins & Monica Grady (In Our Time, Dec. 16, 2004)
- The Journal of the International Society for the History of Philosophy of Science, 2012 (頁面存檔備份,存於網際網路檔案館)
- 科學智慧火花:熱力學第二定律與第二類永動機之錯誤[失效連結]

























































