此條目頁的主題是物理量。關於電路元件,請見「
電容器 」。
感受到電容器 兩端的電位差 ,正電荷與負電荷會分別累積於兩片平行薄板導體。 在電路學 裡,給定電壓 ,電容器 儲存電荷 的能力,稱為電容 (英語:capacitance ),標記為C 。採用國際單位制 ,電容的單位是法拉 (farad ),標記為F 。
平行板電容器 是一種簡單的電容器,是由互相平行、以空間或介電質 隔離的兩片薄板導體 構成。假設這兩片導板分別載有負電荷與正電荷,所載有的電荷量分別為
−
Q
{\displaystyle -Q\,\!}
+
Q
{\displaystyle +Q\,\!}
V
{\displaystyle V}
C
{\displaystyle C}
C
=
Q
V
{\displaystyle C={\frac {Q}{V}}}
由上式知1法拉(Farad)等於1庫侖 (Coulomb)每伏特 (Voltage)。在正常狀況下1法拉的電容多加1伏特的電位差可以多儲存1庫侖的電荷。
電容器所儲存的能量等於充電所做的功 。思考前述平行板電容器,搬移微小電荷元素
d
q
{\displaystyle \mathrm {d} q}
d
W
{\displaystyle \mathrm {d} W}
d
W
=
q
C
d
q
{\displaystyle \mathrm {d} W={\frac {q}{C}}\,\mathrm {d} q}
將這方程式積分,可以得到儲存於電容器的能量。從尚未充電的電容器(
q
=
0
{\displaystyle q=0}
−
Q
{\displaystyle -Q}
+
Q
{\displaystyle +Q}
W
{\displaystyle W}
W
charging
=
∫
0
Q
q
C
d
q
=
Q
2
2
C
=
1
2
C
V
2
=
U
stored
{\displaystyle W_{\text{charging}}=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q={\frac {Q^{2}}{2C}}={\frac {1}{2}}CV^{2}=U_{\text{stored}}}
其中,
U
stored
{\displaystyle U_{\text{stored}}}
電容的單位是法拉,簡稱「法」,單位符號為「F」,是國際單位制導出單位 [1] 庫侖 除以一伏特 。一般來說,1法拉算是很大的電容,大多數用於電子電路 的電容器,其電容會小於法拉幾個數量級,常用的單位有「微法拉」(microfarad,μF),等於
10
−
6
{\displaystyle 10^{-6}}
10
−
9
{\displaystyle 10^{-9}}
微波 工程領域中,有時會使用到較小的「皮法拉」(picofarad,pF),等於
10
−
12
{\displaystyle 10^{-12}}
10
−
15
{\displaystyle 10^{-15}}
1
F
=
10
6
μ
F
=
10
9
n
F
=
10
12
p
F
=
10
15
f
F
.
{\displaystyle 1F=10^{6}\mu F=10^{9}nF=10^{12}pF=10^{15}fF.}
[2]
電容器 [ 編輯 ] 假設,給定電容器的幾何形狀和電容器內部的介質性質,則可以計算出電容。如前圖所示,假設平行板電容器的兩片導板的面積都是
A
{\displaystyle A}
d
{\displaystyle d}
−
σ
{\displaystyle -\sigma }
+
σ
{\displaystyle +\sigma }
σ
=
Q
/
A
{\displaystyle \sigma =Q/A}
應用高斯定律 (詳盡細節,請參閱條目電位移 ),在兩片導板之間的電場
E
{\displaystyle E}
E
=
σ
/
ε
=
Q
/
ε
A
{\displaystyle E=\sigma /\varepsilon =Q/\varepsilon A}
其中,
ε
{\displaystyle \varepsilon }
電容率 。
兩片導板的電位差為
V
=
E
d
=
σ
d
/
ε
=
Q
d
/
ε
A
{\displaystyle V=Ed=\sigma d/\varepsilon =Qd/\varepsilon A}
所以,電容為
C
=
Q
/
V
=
ε
A
/
d
{\displaystyle C=Q/V=\varepsilon A/d}
電容與導板面積A成正比,與導板間隔距離d呈反比,這是在假設平板電容器的面積A相當大的情況下,可以忽略電容器邊緣的效應。假設間隔距離
d
{\displaystyle d}
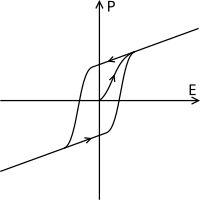
電壓依賴性電容器 [ 編輯 ] 鐵電性物質的電極化強度
P
{\displaystyle P}
E
{\displaystyle E}
遲滯現象 。 許多常用的電介質,其電容率 會隨著外電場的變化而改變,是外電場的函數。鐵電性 物質就是這種電介質。使用這種電介質的電容器,其電容會比較複雜。例如,當這種電容器在充電時,電荷與電壓(電位差)的關係為
d
Q
=
C
(
V
)
d
V
{\displaystyle \mathrm {d} Q=C(V)\ \mathrm {d} V}
在上述方程式裏,電容對於電壓的依賴性
C
(
V
)
{\displaystyle C(V)}
E
=
V
/
d
{\displaystyle E=V/d}
這電場將電介質電極化,從而增加導板儲存電荷的能力。如右圖所示,對於鐵電性物質,電極化強度 對電場曲線顯示出遲滯現象 [3] [4]
假設電極化強度
P
{\displaystyle P}
P
=
f
(
E
)
=
f
(
V
/
d
)
=
g
(
V
)
{\displaystyle P=f(E)=f(V/d)=g(V)}
其中,
f
(
E
)
{\displaystyle f(E)}
g
(
V
)
{\displaystyle g(V)}
well-behaved function )。
根據電位移
D
{\displaystyle D}
D
=
P
+
ϵ
0
E
=
g
(
V
)
+
ϵ
0
V
/
d
{\displaystyle D=P+\epsilon _{0}E=g(V)+\epsilon _{0}V/d}
應用自由電荷高斯定律 ,導板載有的電荷量為
Q
=
D
A
=
(
g
(
V
)
+
ϵ
0
V
/
d
)
A
{\displaystyle Q=DA=(g(V)+\epsilon _{0}V/d)A}
所以,電容為
C
(
V
)
=
Q
V
=
g
(
V
)
A
V
+
ϵ
0
A
d
{\displaystyle C(V)={\frac {Q}{V}}={\frac {g(V)A}{V}}+{\frac {\epsilon _{0}A}{d}}}
假設
g
(
V
)
{\displaystyle g(V)}
g
(
V
)
=
k
V
{\displaystyle g(V)=kV}
k
{\displaystyle k}
C
=
Q
V
=
k
A
+
ϵ
0
A
d
{\displaystyle C={\frac {Q}{V}}=kA+{\frac {\epsilon _{0}A}{d}}}
否則,假設
g
(
V
)
{\displaystyle g(V)}
繼續思考這跟電壓有關的電容,假若將電容器充電至電壓
V
{\displaystyle V}
+
Q
{\displaystyle +Q}
−
Q
{\displaystyle -Q}
Q
=
∫
0
V
C
(
V
′
)
d
V
′
{\displaystyle Q=\int _{0}^{V}C(V')\ \mathrm {d} V'}
當電容與電壓無關時,這方程式變為
Q
=
C
V
{\displaystyle Q=CV}
儲存於電容器 的微分 能量 為
d
U
stored
=
Q
d
V
″
=
[
∫
0
V
″
C
(
V
′
)
d
V
′
]
d
V
″
{\displaystyle \mathrm {d} U_{\text{stored}}=Q\mathrm {d} V''=\left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''}
應用分部積分法 :
∫
a
z
f
(
x
)
g
′
(
x
)
d
x
=
[
f
(
x
)
g
(
x
)
]
a
z
−
∫
a
z
f
′
(
x
)
g
(
x
)
d
x
{\displaystyle \int _{a}^{z}f(x)g'(x)\ \mathrm {d} x=\left[f(x)g(x)\right]_{a}^{z}-\int _{a}^{z}f'(x)g(x)\ \mathrm {d} x}
分別設定
f
(
x
)
=
∫
a
x
h
(
y
)
d
y
{\displaystyle f(x)=\int _{a}^{x}\ h(y)\ \mathrm {d} y}
g
(
x
)
=
x
{\displaystyle g(x)=x}
∫
a
z
∫
a
x
h
(
y
)
d
y
d
x
=
[
∫
a
x
x
h
(
y
)
d
y
]
a
z
−
∫
a
z
x
h
(
x
)
d
x
=
∫
a
z
z
h
(
y
)
d
y
−
∫
a
z
y
h
(
y
)
d
y
=
∫
a
z
(
z
−
y
)
h
(
y
)
d
y
{\displaystyle \int _{a}^{z}\int _{a}^{x}\ h(y)\ \mathrm {d} y\ \mathrm {d} x=\left[\int _{a}^{x}\ xh(y)\ \mathrm {d} y\right]_{a}^{z}-\int _{a}^{z}xh(x)\ \mathrm {d} x=\int _{a}^{z}zh(y)\ \mathrm {d} y-\int _{a}^{z}yh(y)\ \mathrm {d} y=\int _{a}^{z}\ \left(z-y\right)h(y)\ \mathrm {d} y}
設定
x
=
V
″
{\displaystyle x=V''}
y
=
V
′
{\displaystyle y=V'}
h
(
y
)
=
C
(
V
′
)
{\displaystyle h(y)=C(V')}
a
=
0
{\displaystyle a=0}
z
=
V
{\displaystyle z=V}
U
stored
=
∫
0
V
[
∫
0
V
″
C
(
V
′
)
d
V
′
]
d
V
″
=
∫
0
V
(
V
−
V
′
)
C
(
V
′
)
d
V
′
{\displaystyle U_{\text{stored}}=\int _{0}^{V}\ \left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''=\int _{0}^{V}\ \left(V-V'\right)C(V')\ \mathrm {d} V'}
掃描非線性介質顯微鏡 (scanning nonlinear dielectric microscope )的探針掃描於鐵電性物質表面所測量到的非線性電容,可以用來研究鐵電性物質的鐵電疇(ferroelectric domain )結構[5]
有些半導體元件 的電容可以用電壓控制。例如,當變容二極體 的逆向偏壓增加時,空乏層厚度也會增加,因而使得電容降低[6]
頻率依賴性電容器 [ 編輯 ] 假若電容器兩端驅動的含時電壓變化太快,則電介質的電極化強度可能會無法跟上訊號。從微觀層次解釋這機制,在電介質內部,決定電容率的微小電偶極子 無法瞬時地移動,因此,當施加的交流電壓的頻率增加時,電偶極子只能給出有限的響應,從而造成電容率 降低。電容率與頻率的關係稱為介電色散 (dielectric dispersion ),是由介電弛豫 (dielectric relaxation )過程所主控,像德拜弛豫 (Debye relaxation )。從更基本的微觀分析來計算,例如對於介質內的電偶極子行為的微觀分析,處於暫態狀況,電位移場可以表達為(更詳盡細節,請參閱電極化率 )
D
(
t
)
=
ε
0
2
π
∫
−
∞
t
d
t
′
ε
r
(
t
−
t
′
)
E
(
t
′
)
{\displaystyle {\boldsymbol {D}}(t)={\frac {\varepsilon _{0}}{\sqrt {2\pi }}}\int _{-\infty }^{t}\mathrm {d} t'\ \varepsilon _{r}(t-t'){\boldsymbol {E}}(t')}
其中,
ε
0
{\displaystyle \varepsilon _{0}}
電常數 ,
ε
r
=
d
e
f
ε
/
ε
0
{\displaystyle \varepsilon _{r}\ {\stackrel {def}{=}}\ \varepsilon /\varepsilon _{0}}
相對電容率 。
相對電容率的時間依賴可以用線性響應函數 (linear response function )來描述[7]
Δ
t
<
0
{\displaystyle \Delta t<0\,\!}
ε
r
(
Δ
t
)
=
0
{\displaystyle \varepsilon _{r}(\Delta t)=0\,\!}
D
(
t
)
=
ε
0
2
π
∫
−
∞
∞
d
t
′
ε
r
(
t
−
t
′
)
E
(
t
′
)
{\displaystyle {\boldsymbol {D}}(t)={\frac {\varepsilon _{0}}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\mathrm {d} t'\ \varepsilon _{r}(t-t'){\boldsymbol {E}}(t')}
對於時間做傅立葉變換 ,根據摺積定理 ,可以得到
D
(
ω
)
=
ε
0
ε
r
(
ω
)
E
(
ω
)
{\displaystyle {\boldsymbol {D}}(\omega )=\varepsilon _{0}\varepsilon _{r}(\omega ){\boldsymbol {E}}(\omega )}
其中,
ω
{\displaystyle \omega }
角頻率 。
ε
r
(
ω
)
{\displaystyle \varepsilon _{r}(\omega )}
複函數 ,其虛值部分與介質的電場能量吸收有關。更詳盡細節,請參閱條目電容率 。由於電容與電容率成正比,電容也具有這頻率行為。對於時間做傅立葉變換於高斯定律:
Q
(
ω
)
=
∮
S
D
(
r
,
ω
)
⋅
d
a
{\displaystyle Q(\omega )=\oint _{\mathbb {S} }\mathbf {D} (\mathbf {r} ,\omega )\cdot \mathrm {d} \mathbf {a} }
其中,
S
{\displaystyle \mathbb {S} }
Q
{\displaystyle Q}
S
{\displaystyle \mathbb {S} }
r
{\displaystyle \mathbf {r} }
d
a
{\displaystyle \mathrm {d} \mathbf {a} }
流入閉曲面
S
{\displaystyle \mathbb {S} }
I
(
t
)
=
d
Q
d
t
{\displaystyle I(t)={\frac {dQ}{dt}}}
I
(
ω
)
=
j
ω
Q
(
ω
)
=
j
ω
∮
S
D
(
r
,
ω
)
⋅
d
a
=
[
G
(
ω
)
+
j
ω
C
(
ω
)
]
V
(
ω
)
=
V
(
ω
)
Z
(
ω
)
{\displaystyle {\begin{aligned}I(\omega )&=j\omega Q(\omega )=j\omega \oint _{\mathbb {S} }\mathbf {D} (\mathbf {r} ,\omega )\cdot \mathrm {d} \mathbf {a} \\&=\left[G(\omega )+j\omega C(\omega )\right]V(\omega )={\frac {V(\omega )}{Z(\omega )}}\\\end{aligned}}}
其中,
j
{\displaystyle j}
虛數單位 ,
G
(
ω
)
{\displaystyle G(\omega )}
C
(
ω
)
{\displaystyle C(\omega )}
V
(
ω
)
{\displaystyle V(\omega )}
Z
(
ω
)
{\displaystyle Z(\omega )}
電導 、電容、電壓、複值阻抗 。
假設平行板電容器的兩片導板之間填滿了電介質,按照下述關係式,電介質的性質可以測量出來[8]
ε
r
(
ω
)
=
ε
r
′
(
ω
)
−
j
ε
r
″
(
ω
)
=
1
j
ω
Z
(
ω
)
C
0
=
C
(
ω
)
C
0
{\displaystyle \varepsilon _{r}(\omega )=\varepsilon _{r}'(\omega )-j\varepsilon _{r}''(\omega )={\frac {1}{j\omega Z(\omega )C_{0}}}={\frac {C(\omega )}{C_{0}}}}
其中,
ε
r
′
(
ω
)
{\displaystyle \varepsilon _{r}'(\omega )}
ε
r
″
(
ω
)
{\displaystyle \varepsilon _{r}''(\omega )}
C
(
ω
)
{\displaystyle C(\omega )}
C
0
{\displaystyle C_{0}}
自由空間 時的電容)。
深能級暫態譜學 (deep-level transient spectroscopy )利用電容的時間響應來研究半導體 的深能級缺陷[9] 能隙 的位置,缺陷分類為淺能級缺陷和深能級缺陷。淺能級缺陷的能級離導帶 或價帶 的能帶 邊緣比較近,在0.1eV以內,處於這能級的電子或電洞很容易因熱運動而變成自由電子或自由電洞;一般而言,深能級缺陷離能帶邊緣比較遠,超過0.1eV。但也有些物質的深能級缺陷離能帶邊緣雖然只有0.001eV,仍舊能夠顯示出深能級缺陷的通常性質[10]
金屬氧化物半導體電容器 (MOS capacitor )是另一個電容與頻率有關的例子。對於這案例,少數載流子 的緩慢生成意味著在高頻率狀況,只有多數載流子 的響應能夠貢獻出電容,而在低頻率狀況,兩種載流子的響應都能夠貢獻出電容[11] [9]
當頻率為光學 頻率時,半導體 的電容會展示出類似固體的能帶結構。精密的調制光譜學 (modulation spectroscopy )測量方法,使用壓力 或其它種應力 來調制晶體結構,然後觀測光波的吸收或反射的相關變化。這方法貢獻出很多關於這些物質的性質的結果[12]
電容矩陣 [ 編輯 ] 前面論述的範圍局限於兩片任意尺寸、形狀的平行導板的案例。對於單獨的帶電導板,電容的定義方程式
C
=
d
e
f
Q
/
V
{\displaystyle C\ {\stackrel {def}{=}}\ Q/V}
對於多個導體的案例,或當兩個導體所帶淨電荷量不等於零的案例,方程式
C
=
Q
/
V
{\displaystyle C=Q/V}
詹姆斯·馬克士威 提出了「電位係數」和「感應係數」(coefficients of induction )的概念[13]
Q
1
{\displaystyle Q_{1}}
Q
2
{\displaystyle Q_{2}}
Q
3
{\displaystyle Q_{3}}
電位
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
V
3
{\displaystyle V_{3}}
V
1
=
P
11
Q
1
+
P
12
Q
2
+
P
13
Q
3
{\displaystyle V_{1}=P_{11}Q_{1}+P_{12}Q_{2}+P_{13}Q_{3}}
V
2
=
P
21
Q
1
+
P
22
Q
2
+
P
23
Q
3
{\displaystyle V_{2}=P_{21}Q_{1}+P_{22}Q_{2}+P_{23}Q_{3}}
V
3
=
P
31
Q
1
+
P
32
Q
2
+
P
33
Q
3
{\displaystyle V_{3}=P_{31}Q_{1}+P_{32}Q_{2}+P_{33}Q_{3}}
其中,
P
i
j
{\displaystyle P_{ij}}
i
,
j
=
1
,
2
,
3
{\displaystyle i,j=1,2,3}
解析這線性方程組 ,可以得到電荷量分別為
Q
1
=
C
11
V
1
+
C
12
V
2
+
C
13
V
3
{\displaystyle Q_{1}=C_{11}V_{1}+C_{12}V_{2}+C_{13}V_{3}}
Q
2
=
C
21
V
1
+
C
22
V
2
+
C
23
V
3
{\displaystyle Q_{2}=C_{21}V_{1}+C_{22}V_{2}+C_{23}V_{3}}
Q
3
=
C
31
V
1
+
C
32
V
2
+
C
33
V
3
{\displaystyle Q_{3}=C_{31}V_{1}+C_{32}V_{2}+C_{33}V_{3}}
其中,
C
i
i
{\displaystyle C_{ii}}
i
{\displaystyle i}
C
i
j
{\displaystyle C_{ij}}
i
≠
j
{\displaystyle i\neq j}
延伸至
n
{\displaystyle n}
V
i
=
∑
j
=
1
n
P
i
j
Q
j
,
i
=
1
,
2
,
…
,
n
{\displaystyle V_{i}=\sum _{j=1}^{n}P_{ij}Q_{j},\qquad \qquad i=1,2,\dots ,n}
Q
i
=
∑
j
=
1
n
C
i
j
V
j
,
i
=
1
,
2
,
…
,
n
{\displaystyle Q_{i}=\sum _{j=1}^{n}C_{ij}V_{j},\qquad \qquad i=1,2,\dots ,n}
設定第
i
{\displaystyle i}
i
{\displaystyle i}
這樣,整個系統可以用一組係數來描述,稱為「倒電容矩陣」,以方程式定義為
P
i
j
=
d
e
f
∂
V
i
∂
Q
j
{\displaystyle P_{ij}\ {\stackrel {def}{=}}\ {\frac {\partial V_{i}}{\partial Q_{j}}}}
整個系統又可以用另一組係數來描述,稱為「電容矩陣」,以方程式定義為
C
i
j
=
d
e
f
∂
Q
i
∂
V
j
{\displaystyle C_{ij}\ {\stackrel {def}{=}}\ {\frac {\partial Q_{i}}{\partial V_{j}}}}
赫爾曼·馮·亥姆霍茲 和威廉·湯姆森 證明這些電位係數與感應係數都具有對稱性[13]
P
i
j
=
P
j
i
{\displaystyle P_{ij}=P_{ji}}
C
i
j
=
C
j
i
{\displaystyle C_{ij}=C_{ji}}
對於這
n
{\displaystyle n}
−
Q
{\displaystyle -Q\,\!}
+
Q
{\displaystyle +Q\,\!}
Q
{\displaystyle Q\,\!}
[14]
C
=
d
e
f
Q
/
Δ
V
{\displaystyle C\ {\stackrel {def}{=}}\ Q/\Delta V}
假設第
i
{\displaystyle i}
j
{\displaystyle j}
−
Q
{\displaystyle -Q\,\!}
+
Q
{\displaystyle +Q\,\!}
i
{\displaystyle i}
j
{\displaystyle j}
V
i
=
−
P
i
i
Q
+
P
i
j
Q
{\displaystyle V_{i}=-P_{ii}Q+P_{ij}Q}
V
j
=
−
P
j
i
Q
+
P
j
j
Q
{\displaystyle V_{j}=-P_{ji}Q+P_{jj}Q}
這兩個導體的電容為
C
=
Q
/
(
V
j
−
V
i
)
=
1
/
(
P
i
i
+
P
j
j
−
2
P
i
j
)
{\displaystyle C=Q/(V_{j}-V_{i})=1/(P_{ii}+P_{jj}-2P_{ij})}
自電容 [ 編輯 ] 在電路學 裏,電容通常是術語「互電容」(mutual capacitance )的簡稱,即兩個鄰近導體(像平行板電容器的兩片薄板)之間的電容。另外還有一種電路學性質術語「自電容」(self-capacitance ),即單獨導體的電位每增加1V所需的電荷量。設定這電位等於零的參考點為一個理論球殼導體,其半徑為無窮遠,其球心與單獨導體同位置。假設這單獨導體是半徑為
R
{\displaystyle R}
V
=
Q
/
4
π
ε
0
R
{\displaystyle V=Q/4\pi \varepsilon _{0}R}
其自電容是[15]
C
=
Q
/
V
=
4
π
ε
0
R
{\displaystyle C=Q/V=4\pi \varepsilon _{0}R}
范德格拉夫起電機 頂端的圓球形金屬導體,其半徑通常為20 cm,這金屬導體的自電容為
C
=
4
π
ε
0
R
=
4
π
×
8.85
×
10
−
12
×
0.2
≈
22
[
p
F
]
{\displaystyle C=4\pi \varepsilon _{0}R=4\pi \times 8.85\times 10^{-12}\times 0.2\approx 22[pF]}
地球的半徑約為6.378×106 m,其自電容為
C
=
4
π
×
8.85
×
10
−
12
×
6.378
×
10
6
≈
700
[
μ
F
]
{\displaystyle C=4\pi \times 8.85\times 10^{-12}\times 6.378\times 10^{6}\approx 700[\mu F]}
雜散電容 [ 編輯 ] 任意兩個相鄰導體,除非長久保持很近的距離,其電容通常很微小,但仍舊可以被視為電容器。這不受歡迎的效應稱為「雜散電容」。原本各自孤立的電路,由於雜散電容的作用,可能會讓兩個電路互相干擾對方的信號,這效應稱為串擾 。雜散電容是電路在短波波段 正常操作的限制因子。
為了消除跟遠方形成的雜散電容,可以將電路裝置於金屬機殼內,再將金屬機殼跟地線 連結。
簡單系統的電容 [ 編輯 ] 欲求得一個系統的電容,必須先解析拉普拉斯方程式
∇
2
ϕ
=
0
{\displaystyle \nabla ^{2}\phi =0}
ϕ
{\displaystyle \phi }
對於準二維問題,不同的幾何構形之間可以用解析函數互相映射 。詳盡細節,請參閱條目施瓦茨-克里斯托費爾映射
英文名稱 [ 編輯 ] 電容的英文也稱為Capacity。但現在Capacity又另有電量 的意思。[23]
參考文獻 [ 編輯 ]
^ 中華人民共和國國務院. 中华人民共和国法定计量单位 . 維基文庫 . 1984-02-27. ^ 韓瑞功 2004 ,第6頁 harvnb error: no target: CITEREF韓瑞功2004 (help ) ^ Carlos Paz de Araujo, Ramamoorthy Ramesh, George W Taylor (Editors). Science and Technology of Integrated Ferroelectrics: Selected Papers from Eleven Years of the Proceedings of the International Symposium on Integrated Ferroelectrics. CRC Press. 2001. pp. 508–510, Figure 6, 7. ^ Solomon Musikant. What Every Engineer Should Know about Ceramics. CRC Press. 1991: pp. 43, Figure 3.8. ISBN 0824784987 ^ Yasuo Cho. Scanning Nonlinear Dielectric Microscope in Polar Oxides ; R Waser, U Böttger & S Tiedke, editors. Wiley-VCH. 2005. Chapter 16. ISBN 3527405321 ^ Simon M. Sze, Kwok K. Ng. Physics of Semiconductor Devices 3rd Edition. Wiley. 2006. Figure 25, p. 121. ISBN 0470068302 ^ Gabriele Giuliani, Giovanni Vignale. Quantum Theory of the Electron Liquid . Cambridge University Press. 2005: 111 . ISBN 0521821126 ^ Horst Czichos, Tetsuya Saito, Leslie Smith. Springer Handbook of Materials Measurement Methods . Springer. 2006: 475 . ISBN 3540207856 ^ 9.0 9.1 Kasap, Safa; Capper, Peter, Springer handbook of electronic and photonic materials illustrated, Springer: pp. 425, 434–436, 2006, ISBN 9780387260594 ^ Schulz, Max (編), Impurities and defects in Group IV elements and III-V compounds illustrated, Springer: pp. 12 ,68, 1999, ISBN 978-3540179177 ^ Simon M. Sze, Kwok K. Ng. Physics of Semiconductor Devices 3rd Edition. Wiley. 2006: 217. ISBN 0470068302 ^ PY Yu and Manuel Cardona. Fundamentals of Semiconductors 3rd Edition. Springer. 2001: §6.6 Modulation Spectroscopy. ISBN 3540254706 ^ 13.0 13.1 馬克士威, 詹姆斯 , 3, A treatise on electricity and magnetism, Volume 1 , Clarendon Press: pp. 88ff, 1873 ^ Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 43, 88(problem 2.8), 136(problem 3.3), 1999, ISBN 978-0-471-30932-1 ^ 新南威爾斯大學 物理系講義:電容與電介質 網際網路檔案館 的存檔 ,存檔日期2009-02-26.^ 16.0 16.1 Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 88, 1999, ISBN 978-0-471-30932-1 ^ Jackson, J. D. Classical Electrodynamics. Wiley. 1975: 80. ^ Binns; Lawrenson. Analysis and computation of electric and magnetic field problems . Pergamon Press. 1973 [2010-06-04 ] . ISBN 978-0-08-016638-4 ^ 19.0 19.1 Maxwell, J. C. A Treatise on Electricity and Magnetism . Dover. 1873: 266 ff. ISBN 0-486-60637-6 ^ Rawlins, A. D. Note on the Capacitance of Two Closely Separated Spheres. IMA Journal of Applied Mathematics. 1985, 34 (1): 119–120. doi:10.1093/imamat/34.1.119 ^ Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 136, problem 3.3, 1999, ISBN 978-0-471-30932-1 ^ Jackson, J. D. Charge density on thin straight wire, revisited. Am. J. Phys. 200, 68 (9): 789–799. doi:10.1119/1.1302908 ^ Capacity | Definition of Capacity by Merriam-Webster . [2021-01-02 ] . (原始內容 存檔於2021-05-09).



 中华人民共和国法定计量单位. 維基文庫. 1984-02-27.
中华人民共和国法定计量单位. 維基文庫. 1984-02-27.














































![{\displaystyle \mathrm {d} U_{\text{stored}}=Q\mathrm {d} V''=\left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb1d2a38f0054ef11a42860b809646552c2ebac)
![{\displaystyle \int _{a}^{z}f(x)g'(x)\ \mathrm {d} x=\left[f(x)g(x)\right]_{a}^{z}-\int _{a}^{z}f'(x)g(x)\ \mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69a9b2585fbf8bcdf0ee5d636114b1d4396dcab4)


![{\displaystyle \int _{a}^{z}\int _{a}^{x}\ h(y)\ \mathrm {d} y\ \mathrm {d} x=\left[\int _{a}^{x}\ xh(y)\ \mathrm {d} y\right]_{a}^{z}-\int _{a}^{z}xh(x)\ \mathrm {d} x=\int _{a}^{z}zh(y)\ \mathrm {d} y-\int _{a}^{z}yh(y)\ \mathrm {d} y=\int _{a}^{z}\ \left(z-y\right)h(y)\ \mathrm {d} y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf9b9e7b988b1c4db9585e9db925e22393c63765)





![{\displaystyle U_{\text{stored}}=\int _{0}^{V}\ \left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''=\int _{0}^{V}\ \left(V-V'\right)C(V')\ \mathrm {d} V'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582babe2af74f1f54ccecee4c5216f2a9a10aedb)















![{\displaystyle {\begin{aligned}I(\omega )&=j\omega Q(\omega )=j\omega \oint _{\mathbb {S} }\mathbf {D} (\mathbf {r} ,\omega )\cdot \mathrm {d} \mathbf {a} \\&=\left[G(\omega )+j\omega C(\omega )\right]V(\omega )={\frac {V(\omega )}{Z(\omega )}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7facbc4096d73e8bcde1f953fb0871a3552300)












































![{\displaystyle C=4\pi \varepsilon _{0}R=4\pi \times 8.85\times 10^{-12}\times 0.2\approx 22[pF]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33051a38031b72c48c405d897fde7f3b92bc7928)
![{\displaystyle C=4\pi \times 8.85\times 10^{-12}\times 6.378\times 10^{6}\approx 700[\mu F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41fed4732f0cf350e3c3eb275df407b1934fae48)


























![{\displaystyle {\frac {2\pi \varepsilon l}{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+O\left({\frac {1}{\Lambda ^{3}}}\right)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4d56c633ce773c15c52403b1f8c185a95bbbbc)

