五格骨牌

五格骨牌(Pentomino),又稱五連塊、五連方、五連方塊或傷腦筋十二塊,是由五個全等正方形連成的多格骨牌,反射或旋轉視作同一種共有十二種,可以英文字母代表。五格骨牌的相關問題及遊戲是娛樂數學中流行的問題[1]。五格骨牌的謎題,最早是英國人亨利·杜德耐於1907年所發明,書名《坎特伯雷趣题和其他奇特问题》(Canterbury Puzzles and Other Curious Problems)[2]。
五格骨牌中每一個都滿足康威準則,因此用任何一個都可以密鋪整個平面[3]。所有具有對掌性的五格骨牌都可以在不鏡射的條件下密鋪整個平面[4]。
歷史[编辑]

五格骨牌的正式定義是由美國教授所羅門·格倫布在1953年開始定義,後來列在1965年出版的書籍《Polyominoes: Puzzles, Patterns, Problems, and Packings》[1][5]中。之後马丁·加德纳在《科学美国人》雜誌1965年10月的數學遊戲專欄中介紹,引起大家的興趣。格倫布創建了五格骨牌的英文pentomino,源自古希臘語 πέντε / pénte(5),而-omino是採用domino(西洋骨牌),刻意的將domino前面的 d 視為是希臘文字首 di- (二個)的變形。格倫布用12個和五格骨牌外形較類似的英文字母來為五格骨牌命名。
約翰·何頓·康威有另外一個針對五格骨牌命名的系統,其中用O來代替I、Q來代替L、R來代替F、S來代替N。此命名法中,一些五格骨牌和其名稱的關係較不直覺,不過好處是使用了連續的12個英文字母。在討論康威生命游戏時會用到這個命名系統,例如用R骨牌來代替F骨牌。
對稱性[编辑]
- F, L, N, P, Y的骨牌由於既非線對稱亦非點對稱,所以總共有8種固定五格骨牌,旋轉後可以產生四種骨牌,鏡射後再旋轉後可以產生另外四種骨牌,其空間對稱群只有恆等函數。
- T, U的骨牌由於有一條和格線平行的對稱軸,因此只有4種固定五格骨牌。其空間對稱群有二個元素,除了恆等函數外,還包括相對於對稱軸的鏡射。
- V, W的骨牌由於有一條和格線有45度夾角的對稱軸,因此只有4種固定五格骨牌。其空間對稱群有二個元素,除了恆等函數外,還包括相對於對稱軸的鏡射。
- Z的骨牌有一個對稱點,是二次的旋轉對稱,因此也只有4種固定五格骨牌,旋轉後可以產生二種骨牌,鏡射後再旋轉可以產生另外二種骨牌。其空間對稱群有二個元素,除了恆等函數外,也包括180度的旋轉。
- I的骨牌有兩條對稱軸(都平行格線)跟一個對稱點,因此只有2種固定五格骨牌。其空間對稱群有四個元素:恆等函數,兩個鏡射以及180度的旋轉。I的骨牌是 n = 2 的二面體群,也稱為克萊因四元群。
- X的骨牌有四條對稱軸跟一個對稱點,因此只有唯一一種固定五格骨牌。其四條對稱軸分別平行格線以及二條對角線,也有四次的旋轉對稱。其對稱軸是n = 4 的二面體群,有八個元素。
F, L, N, P, Y和Z的骨牌有對掌性,因此若考慮無法翻面的單面骨牌,要加上這些骨牌的鏡射(F', L', N', Q', Y', Z'),共有18種單面骨牌。若骨牌不允許旋轉(固定骨牌),本段分類的第一類要乘以8,後面三類(T、U、V、W、Z)要乘以4,I要算2次,X只算1次,因此共有5×8 + 5×4 + 2 + 1 = 63 個固定的五格骨牌。
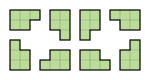
以下是L, F, N, P, Y 骨牌的八種可能放法:
長方形填充[编辑]

標準的五格骨牌謎題是用五格骨牌密鋪長方形,骨牌不能重疊,也不能留下沒有骨牌的空格。每個五格骨牌的面積都等於五個單位方形,因此長方形的面積需等於60個單位方形。可能的尺寸有6×10, 5×12, 4×15 及3×20。狂熱智力游戏玩家可能會徒手玩幾個小時來求解這類問題。另一個問題的挑戰性更大,是計算某一尺寸下有幾種解法,一般會需要配合搜索算法來進行。
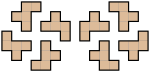
6×10的問題最早是由Colin Brian及Jenifer Haselgrove.[6]所解出,共有2339個解答,2339個解答中,不考慮若將整個長方形旋轉或是鏡射的解,旦若其中部份五格骨牌旋轉或是鏡射,則視為是不同的解。5×12的問題有1010個解,4×15的問題有368個解,3×20的問題只有二個解(圖中的是其中一個解,將L, N, F, T, W, Y, Z方塊組成的方塊組鏡射後,可得到另一個解)。
另一個比較簡單(對稱性較高)的問題,是中間挖掉2×2方塊的8×8正方形,此問題最早由达纳·斯科特在1958年解出[7],共有65種解。斯科特的求解方式也是回溯法電腦程式的早期應用之一。此問題的變體是正方形中的4個空格在其他的位置,大部份的變體都可以解,除非空格都集中在某兩個角附近,讓兩個角都要用P骨牌填充,或是強迫在角落放入T骨牌或U骨牌,使得出現其他五格骨牌無法填滿的格子。
目前已有高效的演算法可求解五格骨牌的密鋪問題,像高德纳也有創建類似的演算法[8]。若在現今的个人电脑上執行,只要幾秒鐘就能解出五格骨牌的擺放方式。
利用所有的n格骨牌來密鋪長方形的問題,只有在n = 0, 1, 2和5時才有解。
平面填充[编辑]
所有12種五格骨牌都滿足康威準則,因此都可以只用同一種五格骨牌,來填滿整個平面。
五立方體及立體填充[编辑]
五立方體(pentacube)是由五個立方體組成的多連立方體,共有29個,其中有12個是高度為1的五格骨牌,另外17個是非平面的。
五立方體填充問題(pentacube puzzle)是由五立方體中12個高度為1的平面五立方體,填滿三維的長方體。五立方體的體積是單位立方體的5倍,要填滿的長方體體積就是單位立方體的60倍,可能的尺寸有2×3×10(12 個解)、2×5×6(264個解)及3×4×5(3940個解 solutions),以下就是這幾種情形的各一個解[9]

五立方體其實有29個,因此也可能會想是否可以用所有的五立方體(包括平面及非平面的)來填滿長方體。不過29個五立方體的體積是單位立方體的29×5=145倍,可能的長方體尺寸只有29×5×1,而高度只有1,無法將非平面的五立方體放入,因此不可能用29個五立方體來填滿長方體。
雙人遊戲[编辑]
以十二塊為基礎,可作一個雙人遊戲。每人輪流在一個8×8的格網上放其中一塊,使得每塊不重疊而沒有一塊用多於一次。最後一個放的人勝。這個遊戲是先手勝的[10]。這個遊戲稱為「格倫布遊戲」[11]。
1960年,桌上遊戲設計師艾力克斯·蘭多夫以此遊戲增加限放規則的補天棋。
建築[编辑]

有時,一些Plattenbau建築的外牆會以以五格骨格為裝飾,主要出現在東歐。圖案主要是以6×10長方形問題的解為主。
腳註[编辑]
- ^ 1.0 1.1 Eric Harshbarger - Pentominoes. [2006-01-18]. (原始内容存档于2020-02-03).
- ^ Pentominoes. [2012-06-09]. (原始内容存档于2017-12-17).
- ^ Rhoads, Glenn C. Planar Tilings and the Search for an Aperiodic Prototile. PhD dissertation, Rutgers University. 2003.
- ^ Gardner, Martin. More about tiling the plane: the possibilities of polyominoes, polyiamonds and polyhexes. Scientific American. 1975-08, 233 (2): 112–115.
- ^ people.rit.edu - Introduction - polyomino and pentomino. [2019-08-17]. (原始内容存档于2020-11-27).
- ^ C. B. Haselgrove; Jenifer Haselgrove. A Computer Program for Pentominoes. Eureka. October 1960, 23: 16–18.
- ^ Dana S. Scott (1958). "Programming a combinatorial puzzle". Technical Report No. 1, Department of Electrical Engineering, Princeton University.
- ^ Donald E. Knuth. "Dancing links" (页面存档备份,存于互联网档案馆) (Postscript, 1.6 megabytes). Includes a summary of Scott's and Fletcher's articles.
- ^ Barequet, Gill; Tal, Shahar. Solving General Lattice Puzzles. Lee, Der-Tsai; Chen, Danny Z.; Ying, Shi (编). Frontiers in Algorithmics. Springer Berlin Heidelberg. 2010: 124–135. doi:10.1007/978-3-642-14553-7_14.
- ^ Hilarie K. Orman. Pentominoes: A First Player Win (页面存档备份,存于互联网档案馆) (Pdf).
- ^ Pritchard (1982),第83頁.
參考資料[编辑]
- Pritchard, D. B. Golomb's Game. Brain Games. Penguin Books. 1982: 83–85. ISBN 0-14-00-5682-3.
相關條目[编辑]
外部連結[编辑]
- Pentomino, Homepage:有各種矩形的全部解
- George Huttlin's Pentomino Webpage:以十二塊砌成英文字母
- Eric Harshbarger's Pentominoes Page (页面存档备份,存于互联网档案馆)
- Pentomino
- 拼圖筆記 My Puzzle Note by 高文山 KAO Wen-Shan from TAIWAN (Note 1 系列貼文詳述:使用12片五格骨牌佈滿正六面體表面的多種方法)
- 這裏可以下載雙人遊戲(Pentacubes)
- 启发积木线上游戏。拖动,旋转和翻转积木瓷砖放在一起的图片或解决数字拼图,玩Tetromino或发现PEG纸牌的解决方案。
| |||||||||||||||||||||||||||