十二面體半形
 | ||
| 類別 | 抽象多胞形 射影多面體 | |
|---|---|---|
| 對偶多面體 | 二十面體半形 | |
| 數學表示法 | ||
| 施萊夫利符號 | {5,3}/2 或 {5,3}5 | |
| 性質 | ||
| 面 | 6 | |
| 邊 | 15 | |
| 頂點 | 10 | |
| 歐拉特徵數 | F=6, E=15, V=10 (χ=1) | |
| 組成與佈局 | ||
| 頂點圖 | 5.5.5 | |
| 對稱性 | ||
| 對稱群 | A5, 60階 | |
| 特性 | ||
| 不可定向、 歐拉示性數為1 | ||
| 圖像 | ||
| ||
在抽象幾何學中,十二面體半形是一種僅由一半數量的正十二面體面構成的抽象多面體。
性質[编辑]
十二面體半形是一種抽象正多面體,共由6個面、15條邊和10個頂點組成;其中所有6個面都是正五邊形、每個頂點都是3個正五邊形的公共頂點,在施萊夫利符號中可以用{5,3}5或{5,3}/2[1]來表示,其中{5,3}代表且每個頂點都是3個正五邊形的公共頂點,然而{5,3}代表正常的正十二面體,因此用{5,3}5符號來表示十二面體半形[2]。十二面體半形的皮特里多邊形為五邊形,且皮特里對偶仍為十二面體半形,是一種自身皮特里對偶的多面體[3]。
構造[编辑]

要構造十二面體半形可透過將正十二面體沿最接近赤道的邊(或沿皮特里多邊形)將其分割成兩半,取其中一個半球,並讓其保持原有連接方式,同時讓赤道(或皮特里多邊形上的)邊與相對邊連結、赤道(或皮特里多邊形上的)點與相對點。這樣的做法產生了一個非實體的抽象多面體,由10個頂點、6個五邊形和15條邊組成,其數量正好為原始正十二面體的一半。在赤道(或皮特里多邊形上)互相交叉連接的作法,使得這個幾何結構的表面成為一個單面且具投影平面連通性的2-流形。[4]
具象化[编辑]
十二面體半形是一個抽象多面體,其無法實體存在,但可以透過一些手段來具象化。2007年,卡羅·塞坎(Carlo Séquin)和詹姆斯·哈姆林(James Hamlin)參考其他不可定向曲面,在SIGGRAPH上發表了一種基於四面體對稱性使用扭歪多邊形面來具象化十二面體半形的方法,並以此研究由十二面體半形組成的四維抽象多胞體——四維正五十七胞體[4]。
然而上述具象化結果是一個扭歪多面體,其面由扭歪五邊形組成,因此無法確定唯一的封閉區域,故無法以「實體」具象化。數學家布蘭科·格倫鮑姆曾提出一個問題:「十二面體半形能否具象化為三維空間自相交之非退化多面體的嵌入?」,這個問題後來由拉約什·希洛西給出了一個可能的解[5][6]。
由於十二面體半形可被視為是一種影射多面體(可視為由六個五邊形構成的實射影平面鑲嵌),因此其亦可以被具象化在一個半球體上。十二面體半形也可以具象化為位於羅馬曲面上的正則地區圖。[7][8][9]
投影[编辑]
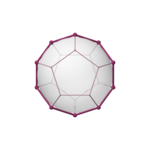
十二面體半形有2種具備對稱性的投影圖,分別為周界為十邊形的投影和周界為十二邊形的投影:[10]
 周界十邊形的投影 |
 周界十二邊形的投影 |
 十二面體半形的另一種投影[3][11] |
佩特森圖[编辑]
在圖論中,十二面體半形可以視為嵌入於實射影平面的佩特森圖[12]。換句話說,即十二面體半形的骨架圖為佩特森圖[3][13]。在這個嵌入的情況下,可以得到其對偶圖為K6(六個頂點的完全圖),對應到二十面體半形。[14]

十二面體半形的六個面於佩特森圖中被繪成塗上顏色的圖形。
相關多面體[编辑]
十二面體半形是一個由6個面組成的抽象多面體。另一個與正十二面體相關,且面數為6的抽象多面體是皮特里十二面體,其拓樸結構是一個位於三階十邊形鑲嵌中,虧格為6的正則地區圖,其可以透過正十二面體的骨架具象化為扭歪多面體。[15]
皮特里十二面體[编辑]
 以不同顏色表示每個面 | |
| 類別 | 皮特里對偶 正則地區圖 |
|---|---|
| 對偶多面體 | C6:{3,10}5 |
| 數學表示法 | |
| 施萊夫利符號 | {5,3}π {10,3}5[15] |
| 性質 | |
| 面 | 6 |
| 邊 | 30 |
| 頂點 | 20 |
| 歐拉特徵數 | F=6, E=30, V=20 (χ=-4) |
| 二面角 | (不存在) |
| 對稱性 | |
| 對稱群 | 點群:Ih, H3, [5,3], *532 作為正則地區圖:A5×C2, 120元素[15] |
| 特性 | |
| 扭歪、正則 | |
皮特里十二面體是正十二面體的皮特里對偶,可以透過將原有正十二面體上取皮特里多邊形構成,換句話說,皮特里十二面體為由正十二面體的皮特里多邊形構成的立體[16]。由於正十二面體的皮特里多邊形為扭歪十邊形,因此無法確立其封閉範圍,故無法計算其表面積和體積。
皮特里十二面體是一種虧格為6的不可定向立體[15],由6個面、30條邊和20個頂點組成,其中,每個面都是扭歪十邊形,每個頂點都是3個扭歪十邊形的公共頂點。[15]
 正十二面體的皮特里多邊形 |
 扭歪十邊形 |
 構成皮特里十二面體的扭歪十邊形面 |
皮特里十二面體與正十二面體互為皮特里對偶,也就是說,皮特里十二面體的皮特里對偶為正十二面體,換句話說,即皮特里十二面體的皮特里多邊形為正五邊形[15][17]。
拓樸結構與皮特里十二面體互相對應的正則地區圖其在施萊夫利符號中可以用{10,3}表示,其意義代表每個頂點都是3個十邊形的公共頂點。其對應的對偶多面體在施萊夫利符號中可以用{3,10}表示,其意義代表每個頂點都是10個三角形的公共頂點,並具有20個面、30條邊和6個頂點[18]。
 皮特里十二面體 |
 以正則地區圖表示的皮特里十二面體 |
參見[编辑]
參考資料[编辑]
- ^ McMullen, Peter and Schulte, Egon. Regular polytopes in ordinary space. Discrete & Computational Geometry (Springer). 1997, 17 (4): 449–478.
- ^ McMullen, Peter; Schulte, Egon, 6C. Projective Regular Polytopes, Abstract Regular Polytopes 1st, Cambridge University Press: 162–165, December 2002, ISBN 0-521-81496-0
- ^ 3.0 3.1 3.2 The hemidodecahedron. Regular Map database - map details. [2021-08-01]. (原始内容存档于2017-03-16).
- ^ 4.0 4.1 Séquin, Carlo and Hamlin, James. The regular 4-dimensional 57-cell. ACM SIGGRAPH 2007 Sketches, SIGGRAPH'07. 2007-08. doi:10.1145/1278780.1278784.
- ^ Szilassi, Lajos. A Polyhedral Model in Euclidean 3-Space of the Six-Pentagon Map of the Projective Plane. Discrete & Computational Geometry (Springer). 2008, 40 (3): 395––400.
- ^ Séquin, Carlo H and Lanier, Jaron and CET, UC. Hyperseeing the regular Hendecachoron. Proc ISAMA (Citeseer). 2007: 159––166.
- ^ Séquin, Carlo H. Regular Maps on Cube Frames. Bridges. 2009.
- ^ Séquin, Carlo H. Symmetrical immersions of low-genus non-orientable regular maps. Symmetry Festival, Delft, the Netherlands, August. 2012: 2––7.
- ^ Séquin, Carlo H; et al. Tubular Sculptures. Bridges Conf. Proc. 2009: 87––96.
- ^ Stokes, Klara and Izquierdo, Milagros. Geometric point-circle pentagonal geometries from Moore graphs. Ars Mathematica Contemporanea. 2015, 11 (1): 215––229.
- ^ Projection of hemidodecahedron. Regular Map database, weddslist.com. [2021-08-01]. (原始内容存档于2021-08-02).
- ^ Planat, Michel, Drawing quantum contextuality with 'dessins d'enfants', 2014-03, ISBN 978-3-319-12945-7, doi:10.1007/978-3-319-12946-4_4
- ^ Balasubramanian, Krishnan. Combinatorics of Petersen graph and its compositions for all irreducible representations for Jahn–Teller, non-rigid molecules and clusters. Journal of Mathematical Chemistry. 2016-08, 54. doi:10.1007/s10910-016-0634-7.
- ^ Melikhov, Sergey A. Combinatorics of embeddings. arXiv preprint arXiv:1103.5457. 2011.
- ^ 15.0 15.1 15.2 15.3 15.4 15.5 C6:{10,3}5. Regular Map database - map details. [2021-07-30].
- ^ Gorini, Catherine A., Geometry at Work, MAA Notes 53, Cambridge University Press: 181, 2000, ISBN 9780883851647
- ^ The dodecahedron. Regular Map database - map details. [2021-07-30]. (原始内容存档于2020-02-01).
- ^ C6:{3,10}5. Regular Map database - map details. [2021-07-30].



