哈密顿图
| 此條目目前正依照fr:Graphe_hamiltonien上的内容进行翻译。 (2021年9月3日) |

哈密顿图(台湾作漢米頓圖)又稱漢密頓圖,是指存在哈密頓環的無向圖,由哈密顿爵士提出。
定義[编辑]
下列定義,既適用於無向圖,亦適用於有向圖。
- 哈密頓路徑
- 圖的一條路,經過每個頂點恰好一次。
- 哈密頓環
- 在一條哈密頓路的基礎上,再有一條邊將其首尾連接,所構成的圈。注意,若有一個哈密頓圈,則移除其任一條邊,皆可得到一條哈密頓路,但反之則不然,即給定一條哈密頓路,不一定能延伸成哈密頓圈,因為該路徑的首尾兩頂點之間,不一定有邊相連。
- 哈密頓圖
- 有哈密頓圈的圖。
- 半哈密頓圖
- 有哈密頓路,但無哈密頓圈的圖。
- 哈密頓連通圖
- 一幅圖,以其任意兩個頂點為起終點,皆存在一條哈密頓路。
- 哈密頓分解
- 將邊集分劃成若干個哈密頓圈。
- 亞哈密頓圖
- 亞哈密頓圖並非哈密頓圖,但只要移除任何一個頂點,就會變成哈密頓圖。
-
非哈密頓圖
-
半哈密頓圖
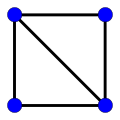
-
哈密頓圖
性質[编辑]
哈密尔顿图的必要条件: 若G=(V,E) 是一个哈密尔顿图,则对于V的每一个非空子集S,均有W(G-S) ≤|S|。其中|S|是S中的顶点数,W(G-S)表示图G擦去属于S中的顶点后,剩下子图的连通分支的个数。
充分條件[编辑]
對歐拉圖而言,有某個充要條件,可用作簡單判定一幅圖是否歐拉圖(歐拉定理)。然而,對於哈密頓圖,並無相應的結果。
不過,仍有一系列越來越鬆的判別條件,能夠斷定一幅圖必定為哈密頓圖。[1]此類定理,最早見於蓋布瑞·狄拉克1952年的研究,其想法直觀,即只要有「足夠多」邊,就能迫得圖有哈密頓圈。用頂點的度推出存在哈密頓圈的定理之中,目前最優的,是1976年邦迪與赫瓦塔爾的定理。
以上是有關無向圖的部分。對於有向圖,相應的定理舉例有Ghouila–Houiri。
狄拉克定理[编辑]
個頂點的簡單圖()中,若每個頂點的度皆至少為,則必為哈密頓圖。
歐爾定理[编辑]
波紹定理[编辑]
波紹·拉約什證明了幾條有關哈密頓圈的定理。以下具體引用一條1962年的定理[4][5],有關連邊少的頂點:
一幅個頂點的完全圖(),若滿足:
- 對所有滿足的整數,度不大於的頂點個數,嚴格小於;
- 度不大於的頂點個數,小於或等於;
則必為哈密頓圖。
注意為偶時,條件2已包含於條件1,所以只在為奇數時,條件2才需要分開列出。

作為例子,考慮附圖中,具有個頂點的圖。其為哈密頓圖:已經將頂點排列好,使哈密頓圈(以紅色標示)正好是外圈。
- 狄拉克定理不足以證明該圖為哈密頓圖。若要應用狄拉克定理,則所有頂點的度皆要至少為,然而圖中有頂點的度僅為。
- 奧爾定理同樣不敷使用,因為圖中標出的兩個不相鄰頂點的度,和僅為,但奧爾定理的條件中,至少要有。
- 另一方面,波紹定理能夠斷定該圖必為哈密頓圖,因為只有個度為的頂點,以及個度為的頂點,故已滿足條件1(因為且)。
例子[编辑]

- 超過2個頂點的完全圖是哈密顿图。階無向完全圖上,不同的(無向)哈密頓圈有個。而若考慮方向,則有個有向哈密頓圈。
- 個頂點的圖當中,最少邊數的哈密頓圖是循環圖。任何循環圖皆為哈密顿图。
- 循環賽圖有奇數條(有向)哈密頓路徑。任意(多於兩個頂點的)循環賽圖為哈密頓圖當且僅當其為強連通。[6]
- 任何以柏拉圖立體(凸正多面體)的邊與頂點構成的圖(「1-骨架」)皆為哈密顿图。[7][8]
- 同樣,棱柱與反棱柱的1-骨架也是哈密頓圖。
- 13種阿基米德立體的1-骨架皆為哈密頓圖,但13種卡塔蘭立體當中,僅有7個的1-骨架是哈密頓圖。[9][10].
- 赫歇爾圖(附圖)是眾多不具哈密頓圈的凸多面體1-骨架當中,最小的一個。[11]
- 哈密頓圖的線圖仍是哈密頓圖。[12]:408
- 歐拉圖的線圖也是哈密頓圖。
哈密顿路径问题[编辑]
寻找哈密顿路径是一个典型的NP-完全问题。后来人们也证明了,找一条哈密顿路的近似比为常数的近似算法也是NP-完全的。
寻找哈密顿路的确定算法虽然很难有多项式时间的,但是这并不意味着只能进行时间复杂度为暴力搜索。利用状态压缩动态规划[來源請求],可以将时间复杂度降低到,具体算法是建立方程f[i][S][j],表示经过了i个节点,节点都是集合S的,到达节点j时的最短路径。每次都按照点j所连的节点进行转移。
參見[编辑]
參考文獻[编辑]
- ^ Melissa DeLeon. Department of Mathematics and Computer Science, Seton Hall University , 编. A Study of Sufficient Conditions for Hamiltonian Cycles (PDF). [2021-09-19]. (原始内容存档 (PDF)于2012-12-22) (英语).
- ^ Dirac, Gabriel Andrew. Some theorems on abstract graphs. Proc. London Math. Soc. 3. 1952, 2: 6––81. MR 0047308. doi:10.1112/plms/s3-2.1.69 (英语).
- ^ Ronald Graham. Handbook of Combinatorics. MIT Press. 1995. ISBN 978-0-262-57170-8 (英语).
- ^ Pósa, Lajos. A theorem concerning hamilton lines. Magyar Tud. Akad. Mat. Kutató ́Int. Közl. 1962, 7: 225–226 (英语).
- ^ Nash-Williams, Crispin. On Hamiltonian circuits in finite graphs (PDF). Proc. Amer. Math. Soc. 1966, 17: 466–467 [2021-09-19]. (原始内容存档 (PDF)于2022-02-17) (英语).
- ^ Graham 1995,第29 & 31頁.
- ^ Gardner, M. "Mathematical Games: About the Remarkable Similarity between the Icosian Game and the Towers of Hanoi." Sci. Amer. 196, 150–156, May 1957. [2021-09-03]. (原始内容存档于2016-10-22).
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Xiong, Liming; Liu, Zhanhong. Hamiltonian iterated line graphs [哈密頓的疊代線圖]. Discrete Mathematics. 2002, 256: 407–422. doi:10.1016/S0012-365X(01)00442-3 (英语).