下面是常用于正交曲线坐标系中的一些向量微积分公式。
- 本文对球坐标使用标准符号ISO 80000-2,它取代了ISO 31-11,(部分其他来源可能有着颠倒θ和φ的定义):
- 极角表示为θ:它是在z轴与连接原点和目标点的径向向量之间的角度。
- 方位角表示为φ:它是在x轴与径向向量在xy面上的投影之间的角度。
- 函数atan2(y, x)可以用于替代数学函数arctan(y/x)。这是由于它的定义域和像的缘故,经典arctan函数的像为(−π/2, +π/2),而atan2定义的像为(−π, π]。
坐标转换[编辑]
在直角、圆柱和球坐标间的变换[1]
|
|
从
|
| 直角
|
圆柱
|
球
|
| 到
|
直角
|

|

|

|
| 圆柱
|

|

|

|
| 球
|

|

|

|
单位向量转换[编辑]
在直角、圆柱和球坐标系间的单位向量转换,从目的坐标的角度。[1]
|
|
直角
|
圆柱
|
球
|
| 直角
|
不適用
|

|

|
| 圆柱
|

|
不適用
|

|
| 球
|

|

|
不適用
|
在直角、圆柱和球坐标系间的单位向量转换,从源坐标的角度。
|
|
直角
|
圆柱
|
球
|
| 直角
|
不適用
|

|

|
| 圆柱
|

|
不適用
|

|
| 球
|

|

|
不適用
|
Del公式[编辑]
在直角、圆柱和球坐标下的del算子的表格
| 运算
|
直角坐标 (x, y, z)
|
圆柱坐标 (ρ, φ, z)
|
球坐标 (r, θ, φ),这里的θ是极角而φ是方位角α
|
| 向量场 A
|

|

|

|
| 梯度 ∇f[1]
|

|

|

|
| 散度 ∇ ⋅ A[1]
|

|

|

|
| 旋度 ∇ × A[1]
|

|

|

|
| 拉普拉斯算子 ∇2f ≡ ∆f[1]
|

|

|

|
| 向量拉普拉斯算子 ∇2A ≡ ∆A
|

|
— 点击查看 [显示] — 
|
— 点击查看 [显示] — 
|
| 物质导数α[2] (A ⋅ ∇)B
|

|

|
— 点击查看 [显示] — 
|
| 张量散度 ∇ ⋅ T
|
— 点击查看 [显示] — 
|
— 点击查看 [显示] — ![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3116bd7e75151c8d599b5e090d2433daffa21069)
|
— 点击查看 [显示] — ![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89522d9531233ee5f0a581ec441bb20c337a13b8)
|
| 微分位移 dℓ[1]
|

|

|

|
| 微分正规面积 dS
|

|

|

|
| 微分体积 dV[1]
|

|

|

|
- ^α 本页对极角采用
 对方位角采用
对方位角采用 ,这是在物理学中常用的符号。某些来源在这些公式中对方位角采用
,这是在物理学中常用的符号。某些来源在这些公式中对方位角采用 对极角采用
对极角采用 ,这是常用数学符号,如果需要这种数学公式,可对换上表公式中的
,这是常用数学符号,如果需要这种数学公式,可对换上表公式中的 和
和 。
。
非平凡的演算规则[编辑]



 (del的拉格朗日公式)
(del的拉格朗日公式)
直角坐标系推导[编辑]
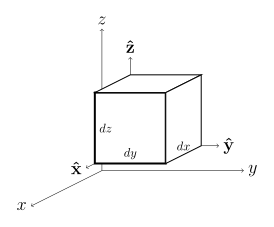


 和
和 的表达式可以同理得出。
的表达式可以同理得出。
註:第一式中的 是
是 在
在 時的量值,並非
時的量值,並非 值乘上
值乘上 。以下圓柱座標、球座標的推導中亦然。
。以下圓柱座標、球座標的推導中亦然。
圆柱坐标系推导[编辑]






球坐标系推导[编辑]
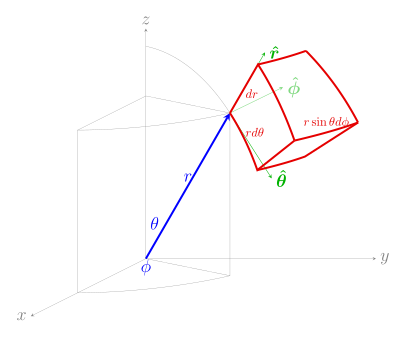





单位向量转换公式[编辑]
坐标参数u的单位向量以如下方式定义,u的小的正值改变导致位置向量 在
在 方向上的改变。因此:
方向上的改变。因此:

这里的s是弧长参数。
对于两组坐标系 和
和 ,依据链式法则:
,依据链式法则:

现在,使除了一个之外的所有 并在两边除以对应的坐标参数的微分,得到:
并在两边除以对应的坐标参数的微分,得到:

外部链接[编辑]












































![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3116bd7e75151c8d599b5e090d2433daffa21069)
![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89522d9531233ee5f0a581ec441bb20c337a13b8)











































