扭棱立方体
 (按這裡觀看旋轉模型) | |||||
| 類別 | 半正多面體 | ||||
|---|---|---|---|---|---|
| 對偶多面體 | 五角二十四面體 | ||||
| 識別 | |||||
| 名稱 | 扭棱立方体 | ||||
| 參考索引 | U12, C24, W17 | ||||
| 鮑爾斯縮寫 | snic | ||||
| 數學表示法 | |||||
| 考克斯特符號 | |||||
| 施萊夫利符號 | sr{4,3} | ||||
| 威佐夫符號 | | 2 3 4 | ||||
| 康威表示法 | sC | ||||
| 性質 | |||||
| 面 | 38 | ||||
| 邊 | 60 | ||||
| 頂點 | 24 | ||||
| 歐拉特徵數 | F=38, E=60, V=24 (χ=2) | ||||
| 組成與佈局 | |||||
| 面的種類 | 正三角形 正方形 | ||||
| 面的佈局 | (8+24)個{3} 6個{4} | ||||
| 頂點圖 | 3.3.3.3.4 | ||||
| 對稱性 | |||||
| 對稱群 | O群 | ||||
| 特性 | |||||
| 對掌性 | |||||
| 圖像 | |||||
| |||||
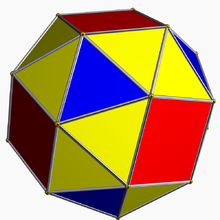
在幾何學中,扭棱立方體(英語:snub cube[1]),又稱擬立方體(英語:cubus simus[2][3])是一種由38個面組成的阿基米德立體[4],由6個正方形和32個正三角形組成,共有60條邊和24個頂點[5]。
性質[编辑]
扭棱立方體是一個手性多面體[6],也就是說,該多面體鏡射之後會跟原本的型形狀不同,無法藉由旋轉半周再回到原本的形狀[7][8][9]。扭棱立方體是一種阿基米德立體,其所有的面都是正多邊形,且每個頂點都是4個三角形和一個正方形,其頂點圖計為3.3.3.3.4或34.4[10],由於所有頂點相等,因此也稱為半正多面體。
體積與表面積[编辑]
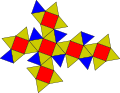
其中t表示三波那契常數:
- 。
由於扭棱立方體由6個正方形和32個正三角形組成,因此其表面積即6倍的正方形面積和32倍的正三角形面積。
二面角[编辑]
扭棱立方體有兩種不同角度的二面角,分別是三角形-三角形二面角和三角形-正方形二面角。其中三角形-三角形二面角餘角的餘弦值是三次方程的零點、三角形-正方形二面角餘角的餘弦值是六次方程的零點。
三角形-三角形二面角以反正割表示為:
換算成角度約為153.23度或153度14分04秒。
三角形-正方形二面角為:
換算成角度約為142.98度或142度59分00秒。
正交投影[编辑]
| 建立於 | 正三角形面 | 正方形面 | 邊 |
|---|---|---|---|
| 圖像 | 
|

|

|
| 投影對稱性 | [3] | [4]+ | [2] |
| 對偶圖像 | 
|

|

|
球面鑲嵌[编辑]
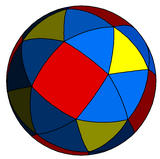
|
 以正方形為中心 |
| 正投影圖 | 球極平面投影 |
|---|
幾何關聯[编辑]

扭棱立方體可透過將立方體的正方形面向外拉,使之不再相連,然後再將正方形面旋轉一個角度,再將空隙以三角形補滿而得
 扭棱立方體 |
 立方體 |
 小斜方截半立方體 |
 扭棱立方體 |
相關多面體及鑲嵌[编辑]
扭棱立方體是立方體經過扭棱變換後的結果,其他也是由立方體透過康威變換得到的多面體有:
| 對稱性: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | c{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
|||||||||
| 對偶多面體 | |||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V4.62/63 | V34.4 | V33 | V3.62 | V35 |
| 原像 |  正四面體 |
 立方體 |
 正八面體 |
 正十二面體 |
 正二十面體 |
|---|---|---|---|---|---|
| 扭稜 |  扭棱四面體 sr{3,3} |

|

| ||
| 扭棱立方体 sr{4,3} |
扭棱八面體 sr{3,4} |
扭棱十二面体 sr{5,3} |
扭棱二十面体 sr{3,5} | ||
| 完全扭稜 |  完全扭稜四面體 β{3,3} |
 完全扭稜立方體 β{4,3} |
 二複合二十面體 β{3,4} |
 完全扭稜十二面體 β{5,3} |
 完全扭稜二十面體 β{3,5} |
參見[编辑]
參考文獻[编辑]
- ^ Wenninger, M. J. "The Snub Cube." Model 17 in Polyhedron Models. Cambridge, England: Cambridge University Press, p. 31, 1989.
- ^ Kepler, J. Harmonices Mundi. 1619. Reprinted Opera Omnia, Lib. II. Frankfurt, Germany. [ASIN B0000DN8M2 網路書源ASIN B0000DN8M2]
- ^ Weissbach, B. and Martini, H. "On the Chiral Archimedean Solids." Contrib. Algebra and Geometry 43, 121-133, 2002.
- ^ Geometry Technologies. "Snub Cube.". scienceu.com. 1999-07-28. (原始内容存档于2000-03-08).
- ^ Weisstein, Eric W. (编). Snub cubic. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ The Snub Cube. eusebeia. 2016-09-09 [2016-08-22]. (原始内容存档于2012-03-16).
- ^ Coxeter, H. S. M., Kaleidoscopes: Selected Writings, John Wiley and Sons: 282, 1995, ISBN 9780471010036.
- ^ Archimedean Solids: Snub Cube (laevo). dmccooey.com. (原始内容存档于2016-03-24).
- ^ Archimedean Solids: Snub Cube (dextro). dmccooey.com. (原始内容存档于2016-03-24).
- ^ Cundy, H. and Rollett, A. "Snub Cube. 3^4.4." §3.7.7 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 107, 1989. ISBN 978-0906212202
外部連結[编辑]
| ||||||||||||
| ||||||||||||||||||||






![{\displaystyle {\tfrac {1+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}}{3}}\approx 1.839\,29}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6384a79e4dc2dc59d706d9662df1968f38208de7)































