格里旺克函数

格里旺克函数（Griewank function）是數學上常用于测试优化程序效率的函数，定义如下：^[1] $G(x_{1},x_{2},\cdots ,x_{n})=1+{\frac {1}{4000}}\sum _{1}^{n}x_{i}^{2}-\prod _{i=1}^{n}cos({\frac {x_{i})}{{\sqrt {(}}i)}}$

一阶格里旺函数[编辑]

$g:=1+(1/4000)*x[1]^{2}-cos(x[1])$

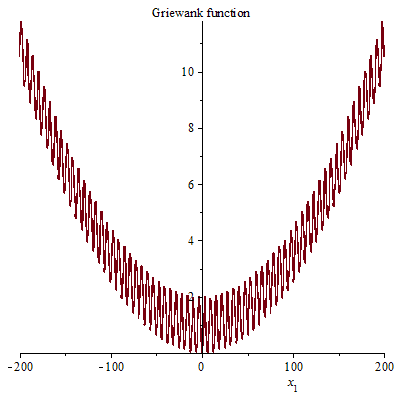
如图所示，一阶格里旺函数有许多极点。^[2]取上述函数的一阶导数，令其为0：

${\frac {1}{2000}}*x[1]+sin(x[1])=0$

用数值解法，求其中在实数域[-100..100]之间的解，共得62个，列出如下：

[-97.438110610025603200, -94.200661844477748520, -91.151778636270389965, -87.920619819329359985, -84.865447114417916660, -81.640577359698817225, -78.579116013127494725, -75.360534496781834905, -72.292785301096032350, -69.080491261738200370, -66.006454947055212230, -62.800447685694571355, -59.720124919768677970, -56.520403799747265470, -53.433795188029228405, -50.240359634965042195, -47.147465720656019171, -43.960315222391878044, -40.861136486491770843, -37.680270593049735600, -34.574807454399982858, -31.400225777941327138, -28.288478593262152626, -25.120180808052873462, -22.002149871974999083, -18.840135714356858698, -15.715821259447690012, -12.560090527814781691, -9.4294927245990724370, -6.2800452793799046870, -3.1431642363549054240, 3.1431642363549054240, 6.2800452793799046870, 9.4294927245990724370, 12.560090527814781691, 15.715821259447690012, 18.840135714356858698, 22.002149871974999083, 25.120180808052873462, 28.288478593262152626, 31.400225777941327138, 34.574807454399982858, 37.680270593049735600, 40.861136486491770847, 43.960315222391878044, 47.147465720656019171, 50.240359634965042195, 53.433795188029228405, 56.520403799747265470, 59.720124919768677970, 62.800447685694571355, 66.006454947055212230, 69.080491261738200370, 72.292785301096032350, 75.360534496781834905, 78.579116013127494725, 81.640577359698817225, 84.865447114417916660, 87.920619819329359985, 91.151778636270389965, 94.200661844477748520, 97.438110610025603200, 0.]

在[-10000,10000]区间，极点个数=6365

二阶格里旺函数[编辑]

$g2:=1+(1/4000)*x[1]^{2}+(1/4000)*x[2]^{2}-cos(x[1])*cos((1/2)*x[2]*{\sqrt {(}}2))$

三阶格里旺函数[编辑]

${1+(1/4000)*x[1]^{2}+(1/4000)*x[2]^{2}+(1/4000)*x[3]^{2}-cos(x[1])*cos((1/2)*x[2]*{\sqrt {(}}2))*cos((1/3)*x[3]*sqrt(3))}$

参考文献[编辑]

^ Griewank, A. O. "Generalized Decent for Global Optimization." J. Opt. Th. Appl. 34, 11-39, 1981
^ Locatelli, M. "A Note on the Griewank Test Function." J. Global Opt. 25, 169-174, 2003

[1] Griewank, A. O. "Generalized Decent for Global Optimization." J. Opt. Th. Appl. 34, 11-39, 1981

[2] Locatelli, M. "A Note on the Griewank Test Function." J. Global Opt. 25, 169-174, 2003

[1]

[2]

一阶格里旺函数[编辑]

二阶格里旺函数[编辑]

三阶格里旺函数[编辑]

相關條目[编辑]

参考文献[编辑]