 伯努利雙紐線的外形如∞
伯努利雙紐線的外形如∞
環面曲線(toric section)是平面和環面相交形成的曲線,正如圓錐曲線是圓錐面和平面相交而成的。其方程為:

它們都是四次曲線。
伯努利雙紐線[编辑]
伯努利雙紐線(Lemniscate of Bernoulli)的方程為

求雙紐線的弧長需要應用橢圓積分。雙紐線可視為雙曲線的反演變換,反演圓心在双曲线的中心。
卡西尼卵形線[编辑]
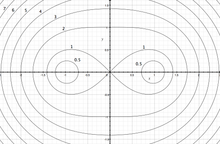 卡西尼卵形線
卡西尼卵形線
取兩個定點 為焦點。卡西尼卵形線(Cassini oval)是所有這樣的點P的軌跡:
為焦點。卡西尼卵形線(Cassini oval)是所有這樣的點P的軌跡: 和焦點的距離的積為常數(這類似橢圓的定義——點
和焦點的距離的積為常數(這類似橢圓的定義——點 和焦點的距離的和為常數)。即
和焦點的距離的和為常數)。即 。
。
在直角坐標系,若焦點分別在 和
和 ,卵形線的方程可寫成:
,卵形線的方程可寫成:



在極坐標系:

卵形線經過反演變換,依然是卵形線。
卵形線的形狀由 的值決定。若
的值決定。若 ,軌跡是一個封閉的圈。若
,軌跡是一個封閉的圈。若 ,軌跡是兩個封閉的圈。若
,軌跡是兩個封閉的圈。若 ,軌跡為伯努利雙紐線。
,軌跡為伯努利雙紐線。
Hippopede曲線[编辑]
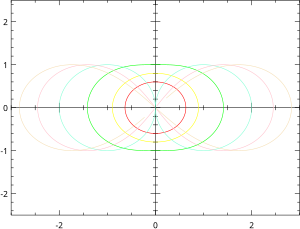 Hippopedes: a=1, b=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
Hippopedes: a=1, b=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
 Hippopedes: b=1, a=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
Hippopedes: b=1, a=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
Hippopede曲線(或Hippopede of Proclus)的極坐標方程為:

直角坐標系:

當 ,Hippopede曲線為伯努利雙紐線。
,Hippopede曲線為伯努利雙紐線。






















