多边形二面体
 多边形二面体的例子:球面上的六边形二面体 | |
| 类别 | 均匀多面体 球面镶嵌 |
|---|---|
| 对偶多面体 | 多面形 |
| 数学表示法 | |
| 考克斯特符号 | |
| 施莱夫利符号 | {n,2} |
| 威佐夫符号 | 2 | n 2 |
| 性质 | |
| 面 | |
| 边 | |
| 顶点 | |
| 欧拉特征数 | F=, E=, V= (χ=2) |
| 组成与布局 | |
| 面的种类 | n边形 |
| 顶点布局 | n2 |
| 对称性 | |
| 对称群 | Dnh, [2,n], (*22n), order 4n |
| 旋转对称群 | Dn, [2,n]+, (22n), order 2n |
| 注:为底面边数 。 | |
多边形二面体是由2个多边形面组成的多面体,是一种二面体,为由两个共用相同的一组边的多边形面组成的多面体。在三维欧几里德空间中,如果它的面是平的,就会属于退化的多面体,即与多边形相同,并不具有体积;而在三维球面中,与平面的两面体可以认为是透镜,它的一个例子是一个透镜空间L(p,q)的基本域。[1]多边形二面体也可以被称为双面体(bihedra)[2]、平面多面体(flat polyhedra)[3]或二重复盖多边形(doubly covered polygons)[3]。
通常一个普通的二面体隐含的意义是多边形(2正多边形叠在一起),因此施莱夫利符号中利用{n,2}来表示。[4]
多边形二面体可以作为一个球面镶嵌以非退化的形式存在,其由2个n条边的面覆盖整个球面,每个面恰好占据一个半球,顶点位于球面的大圆上。若这个球面镶嵌的多边形二面体顶点的间距相等,那么这个几何结构就是正图形,称为正多边形二面体。
n边形二面体的对偶多面体为n面形,由n个二角形共用两个顶点组成。
多边形二面体可以截半为多香肠面形(lucanicohedron)。[5]
作为平面多面体[编辑]
多边形二面体可以被认为是退化的柱体,其两个底面直接“背对背”地连接起来,且没有侧面,因此这个柱体将没有高度,也无法拥有体积。组成多边形二面体的两个多边形必须是全等的,其若要能顺利地以上述方式连接的话,这两个多边形必须互为镜像。这只适用于两个面之间的距离为零的情况;两个面距离大于零的情况只在其面为无限的多边形时(有点类似无限面形的二角形面,其宽度大于零,为无限延伸的条纹)。
多边形二面体也可以从亚历山德罗夫唯一性定理中产生,该定理将任何凸多面体的表面上的距离以局部欧几里得空间化的模式来计算,除了有有限数量角亏之和为4π的点。 这一特性也适用于多边形二面体表面的距离,因此亚历山德罗夫唯一性定理的陈述要求将多边形二面体视为凸多面体。[6]
有些多边形二面体可以作为一些多面体类型之系列的最初项存在,例如:底面为二角形的柱体是正方形二面体、底面为二角形的锥体是三角形二面体。
正多边形二面体可以视为一种退化的正多面体,其在施莱夫利符号中以{n,2}表示,由2个施莱夫利符号表示为{n}的正多边形组成,其中,n为正多边形的边数,也就是正n边形。[7]
作为球面镶嵌[编辑]
球面的多边形二面体由2个球形多边形组成,其在球面的大圆上共用n个相同的顶点;球面多边形二面体的每个多边形面都恰好填满了一个半球。
球面正多边形二面体由两个球面正多边形组成,这两个球面正多边形在球面的大圆上共用n个相同的顶点,并在大圆赤道上等距分布。
施莱夫利符号记为{2,2}的多面体是一个自身对偶的多面体,它既是多面形(二面形)也是多边形二面体(二角形二面体)。
| 空间 | 球面 | 欧几里得 | |||||||
|---|---|---|---|---|---|---|---|---|---|
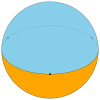
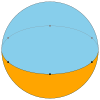
| 名称 | 零角形二面体 | 一角形二面体 | 二角形二面体 | 三角形二面体 | 正方形二面体 | 五边形二面体 | 六边形二面体 | ... | 无限边形二面体 |
| 图像 | 
|

|

|
|

|

|
|
... | 
|
| 施莱夫利 | {0,2} | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | {6,2} | ... | {∞,2} |
| 考克斯特 | ... | ||||||||
| 面 | 2 {0} | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | 2 {6} | ... | 2 {∞} |
| 边和 顶点 |
0个顶点 1条边 |
1 | 2 | 3 | 4 | 5 | 6 | ... | ∞ |
| 对偶多面体 | 零面体[注 1] | 一面形 | 二面形 | 三面形 | 四面形 | 五面形 | 六面形 | ... | 无限面形 |
无限边形二面体[编辑]
当多边形二面体的边数多达正无穷大时,则会出现不一样的特性:该几何结构不再是面互相背对背贴合的平面多面体,也不是球面镶嵌,而是一个可以填满整个平面的平面镶嵌图,其又称为二阶无限边形镶嵌。
多胞形二胞体[编辑]
正多胞形二胞体是多边形二面体在n维空间的类比,其施莱夫利符号记为{p,...,q,r,2},由2个施莱夫利符号记为{p,...,q,r}的维面组成,并且共用施莱夫利符号记为{p,...,q}的维脊。[9]
相关几何图形[编辑]
| 球面镶嵌 | 二面体 | 欧式镶嵌 仿紧空间 |
双曲镶嵌 非紧空间 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
{1,2} |
 {2,2} |
{3,2} |
 {4,2} |
{5,2} |
 {6,2} |
 {7,2} |
 {8,2} |
... |
 {∞,2} |
 {iπ/λ,2} |
截角多边形二面体[编辑]

截角多边形二面体是指经过截角变换的多边形二面体。n边形二面体由两个n边形背对背贴合组成,而截角之后,n边形会变成2n边形,并且在原有的顶点处形成二角形截面,因此n边形二面体为由2个2n边形背对背贴合组成,且贴合的棱处有n个二角形交错地出现,没有二角形的2n边形-2n边形贴合处则是直接贴合,因此其顶点为两个2n边形和一个二角形的公共顶点。例如截角三角形二面体,其由2个六边形和3个二角形组成,这3个二角形交错地出现在六边形周围。
参见[编辑]
注释[编辑]
参考文献[编辑]
- ^ Gausmann, Evelise; Roland Lehoucq, Jean-Pierre Luminet, Jean-Philippe Uzan, Jeffrey Weeks. Topological Lensing in Spherical Spaces. Classical and Quantum Gravity. 2001, 18: 5155–5186. arXiv:gr-qc/0106033
 . doi:10.1088/0264-9381/18/23/311.
. doi:10.1088/0264-9381/18/23/311.
- ^ Kántor, S., On the volume of unbounded polyhedra in the hyperbolic space (PDF), Beiträge zur Algebra und Geometrie, 2003, 44 (1): 145–154 [2017-02-14], MR 1990989, (原始内容 (PDF)存档于2017-02-15).
- ^ 3.0 3.1 O'Rourke, Joseph, Flat zipper-unfolding pairs for Platonic solids, 2010, Bibcode:2010arXiv1010.2450O, arXiv:1010.2450

- ^ Weisstein, Eric W. (编). Dihedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Draghicescu, Mircea. Building Polyhedra Models for Mathematical Art Projects and Teaching Geometry (PDF). Proceedings of Bridges 2019: Mathematics, Art, Music, Architecture, Education, Culture. 2019: 629–634 [2022-12-28]. (原始内容存档 (PDF)于2022-12-23).
- ^ O'Rourke, Joseph, On flat polyhedra deriving from Alexandrov's theorem, 2010, Bibcode:2010arXiv1007.2016O, arXiv:1007.2016

- ^ Coxeter, H. S. M., Regular Polytopes 3rd, Dover Publications Inc.: 12, January 1973, ISBN 0-486-61480-8
- ^ G. S. Anagnostatos. On the Possible Stability of Tetraneutron and Hexaneutron. HNPS Proceedings. 2020-02-20, 13: 313 [2021-08-12]. ISSN 2654-0088. doi:10.12681/hnps.2981. (原始内容存档于2021-08-12).
- ^ McMullen, Peter; Schulte, Egon, Abstract Regular Polytopes 1st, Cambridge University Press: 158, December 2002, ISBN 0-521-81496-0
- 参考书目
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
外部链接[编辑]
| |||||||||||||||||||||||||||||||||||||||||||||||||



