星形四角化菱形十二面体

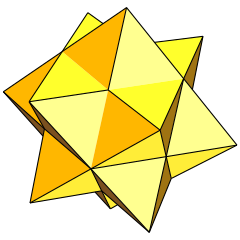**星形四角化菱形十二面体**
	; （按这里观看STL模型）
类别	艾雪立体; 星形菱形十二面体; 星形多面体
数学表示法
康威表示法	k(h=0.76)KjC
性质
面	48
边	72
顶点	26
欧拉特征数	F=48, E=72, V=26 （χ=2）
组成与布局
面的种类	简单多面体：等腰三角形复杂多面体：非凸六边形
对称性
对称群	Oh, B3, [4,3], *432
旋转对称群; （英语：Rotation_groups）	O, [4,3]+, (432)
特性
	面可递
	查; 论; 编;

在几何学中，星形四角化菱形十二面体又称为第一种星形菱形十二面体（First stellation of rhombic dodecahedron），是一种星形菱形十二面体，菱形十二面体的星形化体之一，也是空间填充多面体之一^[2]。在艺术领域中，这种形状又称为艾雪立体（Escher's Solid）^[3]^[4]，出现于莫里兹·柯尼利斯·艾雪的作品《瀑布》和一个研究艾雪作品《群星》的研究中。

性质[编辑]

星形四角化菱形十二面体共有三种形式，第一种为菱形十二面体的星形化体，共有12个面，面的几何中心位置与菱形十二面体相同。第二种为简单多面体，由48个等腰三角形组成，可以视为在菱形十二面体的每个面上叠上一个菱形锥来构成。星形四角化菱形十二面体共有26个顶点和72条边，在26个顶点中，其中有6个顶点度为8, 、8个顶点度为6和12个度为4的顶点。在72条边中有48条长边和24条较短的边。对应的欧拉示性数26 + 48 − 72 = +2。最后一种是3个双四角锥的复合体^[6]^[7]。


第一种菱形十二面体的星形化体	48个等腰三角形组成的简单多面体	3个扁八面体的复合体

此外，星形四角化菱形十二面体可以独立填满三维空间^[8]^[9]，所构成的几何结构为星形四角化菱形十二面体堆砌。

星形四角化菱形十二面体的骨架图为四角化菱形十二面体图^[10]。

体积与表面积[编辑]

一个最短边边长为a的星形四角化菱形十二面体，其表面积A、体积V为^[10]：

{\begin{aligned}A&=16{\sqrt {2}}\,a^{2}\approx 22.6274\,a^{2}\\V&={\tfrac {32{\sqrt {3}}}{9}}a^{3}\approx 6.1584\,a^{3}\end{aligned}}

若一个最长边边长为单位长，则其体积为4^[11]，若最长边的边长为a，则体积为：^[12]

V=4a^{3}

面的组成[编辑]

星形四角化菱形十二面体作为一个简单多面体时由48个全等的等腰三角形组成；作为一个星形多面体时由12个非凸六边形组成；作为一个复合立体时由3个双四角锥组成^[7]：

等腰三角形	非凸六边形
48个等腰三角形组成的简单多面体	第一种菱形十二面体的星形化体

若每个等腰三角形底边为1，则两侧边的边长为 ${\frac {\sqrt {3}}{2}}$ ^[11]。

顶点坐标[编辑]

若一个星形四角化菱形十二面体最长边长为单位长且几何中心位于原点，则其顶点坐标为^[13]：

\left(\pm 1\,,\quad 0\,,\quad 0\right)

、

\left(0\,,\quad \pm 1\,,\quad 0\right)

、

\left(0\,,\quad 0\,,\quad \pm 1\right)

\left(0\,,\quad \pm 1\,,\quad \pm 1\right)

、

\left(\pm 1\,,\quad 0\,,\quad \pm 1\right)

、

\left(\pm 1\,,\quad \pm 1\,,\quad 0\right)

\left(\pm {\frac {1}{2}}\,,\quad \pm {\frac {1}{2}}\,,\quad \pm {\frac {1}{2}}\right)

历史[编辑]

1957年多尔曼·露可（Dorman Luke）在他的论文中描述了一些菱形十二面体的星形化体^[14]。1961年，星形四角化菱形十二面体被艾雪描绘在其作品《瀑布》中^[15]。1986年，阿瑟斯·洛布（Arthur Loeb）发表了一篇针对艾雪作品《群星》的研究，其探讨了星形四角化菱形十二面体的性质^[16]，然而《群星》中所出现的形状不是星形四角化菱形十二面体而是三复合正八面体^[17]。后续的研究指出《瀑布》和《群星》中出现的2个相似的形状是不同的形状，前者是星形四角化菱形十二面体，后者是三复合正八面体^[7]。1971年吉本直贵发现了由两个星形菱形十二面体拼凑成立方体的结构，并利用其发表了一种可以变形成星形四角化菱形十二面体的吉本魔方^[18]。

相关多面体与镶嵌[编辑]

星形四角化菱形十二面体可以将菱形十二面体透过四角化变换来完成，其等价于将菱形十二面体每个面替换成一个顶点和四个三角形^[19]，而菱形十二面体是一个由立方体透过康威变换的结果。其他也是由立方体透过康威变换的形状有：

半正正八面体家族多面体
对称性: [4,3], (*432)							[4,3]⁺, (432)	[1⁺,4,3], (*332)	[4,3⁺], (3*2)


{4,3}	t_0,1{4,3}	t₁{4,3}	t_1,2{4,3}	{3,4}	t_0,2{4,3}	t_0,1,2{4,3}	s{4,3}	h{4,3}	h_1,2{4,3}
半正多面体的对偶


V4.4.4	V3.8.8	V3.4.3.4	V4.6.6	V3.3.3.3	V3.4.4.4	V4.6.8	V3.3.3.3.4	V3.3.3	V3.3.3.3.3


菱形十二面体	四角化菱形十二面体	星形四角化菱形十二面体	反平行四边形二十四面体

星形四角化菱形十二面体是一种星形菱形十二面体，其他星形菱形十二面体有^[2]：

星形化次数	0	1	2
名称	菱形十二面体	艾雪立体	(未获命名)
图像
星状图

星形四角化菱形十二面体堆砌[编辑]

星形四角化菱形十二面体可以独立填满三维空间^[8]^[20]，其所形成的几何结构称为星形四角化菱形十二面体堆砌。

北炯立体[编辑]

哲养·北炯曾在其论文中探讨星形十二面体^[21]，但不慎将以五边形组成的正十二面体之星形化体与菱形组成的菱形十二面体之星形化体搞混了。后来莫雷帝将其描述为在正十二面体的面上加入五角锥组成的立体^[22]，即小星形十二面体。汉士·史梅斯特（Hans Smessaert）等人才以星形四角化菱形十二面体的结构完成北炯最初探讨的议题^[23]。后来在部分文献中，这种立体被称为北炯立体（Béziau's solid）或北炯的星形菱形十二面体（Béziau's stellar rhombic dodecahedron）。

莫雷帝描述的北炯立体	汉士·史梅斯特描述的北炯立体

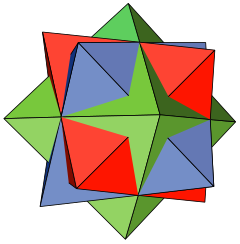
三复合正八面体[编辑]

三复合正八面体是一个外观与星形四角化菱形十二面体十分相似的形状，皆出现于艾雪的木版画中。^[7]^[24]

四角化菱形十二面体[编辑]

星形四角化菱形十二面体与四角化菱形十二面体皆为菱形十二面体透过四角化变换后的结果，差别只在四角化时在面上加入之菱形锥的锥高不同，四角化菱形十二面体为加入的菱形锥^[19]，且其锥高不超过外接球的结果。

四角化菱形十二面体	星形四角化菱形十二面体

参见[编辑]

吉本魔方

参考文献[编辑]

^ Chris (Kit) Wallace. Escher's Solid. kitwallace.co.uk. [2019-09-09].
^ ^2.0 ^2.1 George Hart. Stellations. georgehart.com. [2019-09-06]. （原始内容存档于2018-11-30）.
^ Berger, Jonathan Bernard, The Design and Modeling of Periodic Materials with Novel Properties (PDF), UC Santa Barbara, 2014 [2019-11-14], （原始内容存档 (PDF)于2019-09-22）
^ Escher, Maurits Cornelis, The Info List-MC Escher, TheInfoList.com
^ ^5.0 ^5.1 Silva, Ederson Marcelino da; et al, Poliedros de Arquimedes, Catalan, Kepler-Poinsot, Platão e o Sólido de Escher: contribuições para o ensino e aprendizagem de poliedros (PDF), Universidade Tecnológica Federal do Paraná, 2018
^ Silva, Ederson Marcelino da, Poliedros de Arquimedes, Catalan, Kepler-Poinsot, Platão e o Sólido de Escher: contribuições para o ensino e aprendizagem de poliedros,^[5] 2018: p.60
^ ^7.0 ^7.1 ^7.2 ^7.3 The compound of three octahedra and a remarkable compound of three square dipyramids, the Escher's solid （页面存档备份，存于互联网档案馆）, Livio Zefiro, University of Genova.
^ ^8.0 ^8.1 Ioana Mihaila. Tessellations from Group Actions and the Mystery of Escher’s Solid (PDF). [2013-05-09]. （原始内容存档于2013-06-27）.
^ US patent 9370765,Peter Haaland,“Space-filling polyhedral sorbents”,发表于2016-06-21,发行于2016-06-21,指定于Innerproduct Partners Fund Lp , US 2016/0096164 A1 (PDF). [2019-09-09]. Suitable regular shaped space-filling polyhedra includ, but are not limited to, an acute golden rhombohedron, ...... an Escher's solid, ......and a truncated octahedron.
^ ^10.0 ^10.1 Weisstein, Eric W. (编). Escher's Solid. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
^ ^11.0 ^11.1 David I. McCooey. Other Solids: Escher's Solid. dmccooey.com. 2015 [2019-09-02]. （原始内容存档于2019-09-05）.
^ Silva, Ederson Marcelino da, Poliedros de Arquimedes, Catalan, Kepler-Poinsot, Platão e o Sólido de Escher: contribuições para o ensino e aprendizagem de poliedros,^[5] 2018: p.85
^ Data of Escher's Solid. dmccooey.com. （原始内容存档于2019-09-05）.
^ Luke, D. Stellations of the rhombic dodecahedron. The Mathematical Gazette. 1957, 337: 189–194.
^ Bool, F. H.; Kist, J. R.; Locher, J. L.; and Wierda, F., M. C. Escher: His Life and Complete Graphic Work, New York: Harry N. Abrams, Inc.: p.323, 1992年9月1日, ISBN 9780810981133
^ Arthur Loeb, "Polyhedra in the Work of M.C. Escher," in Coxeter et al. (eds.), M.C. Escher: Art and Science, 1986.
^ George Hart. The Polyhedra of M.C. Escher. [2019-09-05]. （原始内容存档于2019-01-15）.
^ Yoshimoto Cube No. 1 | MoMA Design Store. Museum of Modern Art Store. [20 August 2018]. （原始内容存档于2019-09-05）.
^ ^19.0 ^19.1 Hexakis Octahedron. Florida Center for Instructional Technology, College of Education, University of South Florida. [2019-09-03]. （原始内容存档于2015-01-21）.
^ Alan Holden, Shapes, Space and Symmetry, Columbia University Press, NY, 1971.
^ Béziau, Jean-Yves. New light on the square of oppositions and its nameless corner. Logical Investigations. 2003, 10 (2003): 218––232.
^ Moretti, Alessio. The critics of paraconsistency and of many-valuedness and the geometry of oppositions. Logic and Logical Philosophy. 2010, 19 (1-2): 63––94.
^ Smessaert, Hans and Demey, Lorenz, Béziau’s contributions to the logical geometry of modalities and quantifiers, The road to universal logic (Springer), 2015: 475––493
^ Coxeter, H. S. M., A special book review: M. C. Escher: His life and complete graphic work, The Mathematical Intelligencer, 1985, 7 (1): 59–69, doi:10.1007/BF03023010 Coxeter's analysis of Stars is on pp. 61–62.

外部链接[编辑]

埃里克·韦斯坦因. 星形四角化菱形十二面體. MathWorld.

[1] Chris (Kit) Wallace. Escher's Solid. kitwallace.co.uk. [2019-09-09].

[George_Hart_Stellations-4] 2.0 ^2.1 George Hart. Stellations. georgehart.com. [2019-09-06]. （原始内容存档于2018-11-30）.

[phdthesis_berger2014design-5] Berger, Jonathan Bernard, The Design and Modeling of Periodic Materials with Novel Properties (PDF), UC Santa Barbara, 2014 [2019-11-14], （原始内容存档 (PDF)于2019-09-22）

[article_escherinfo-6] Escher, Maurits Cornelis, The Info List-MC Escher, TheInfoList.com

[mastersthesis_silva2018poliedros-7] 5.0 ^5.1 Silva, Ederson Marcelino da; et al, Poliedros de Arquimedes, Catalan, Kepler-Poinsot, Platão e o Sólido de Escher: contribuições para o ensino e aprendizagem de poliedros (PDF), Universidade Tecnológica Federal do Paraná, 2018

[8] Silva, Ederson Marcelino da, Poliedros de Arquimedes, Catalan, Kepler-Poinsot, Platão e o Sólido de Escher: contribuições para o ensino e aprendizagem de poliedros,^[5] 2018: p.60

[Livio_Zefiro_2010-9] 7.0 ^7.1 ^7.2 ^7.3 The compound of three octahedra and a remarkable compound of three square dipyramids, the Escher's solid （页面存档备份，存于互联网档案馆）, Livio Zefiro, University of Genova.

[Ioana_Mihaila_2005-10] 8.0 ^8.1 Ioana Mihaila. Tessellations from Group Actions and the Mystery of Escher’s Solid (PDF). [2013-05-09]. （原始内容存档于2013-06-27）.

[11] US patent 9370765,Peter Haaland,“Space-filling polyhedral sorbents”,发表于2016-06-21,发行于2016-06-21,指定于Innerproduct Partners Fund Lp , US 2016/0096164 A1 (PDF). [2019-09-09]. Suitable regular shaped space-filling polyhedra includ, but are not limited to, an acute golden rhombohedron, ...... an Escher's solid, ......and a truncated octahedron.

[Mathworld_EschersSolid-12] 10.0 ^10.1 Weisstein, Eric W. (编). Escher's Solid. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.

[dmccooey_Escher-13] 11.0 ^11.1 David I. McCooey. Other Solids: Escher's Solid. dmccooey.com. 2015 [2019-09-02]. （原始内容存档于2019-09-05）.

[14] Silva, Ederson Marcelino da, Poliedros de Arquimedes, Catalan, Kepler-Poinsot, Platão e o Sólido de Escher: contribuições para o ensino e aprendizagem de poliedros,^[5] 2018: p.85

[15] Data of Escher's Solid. dmccooey.com. （原始内容存档于2019-09-05）.

[16] Luke, D. Stellations of the rhombic dodecahedron. The Mathematical Gazette. 1957, 337: 189–194.

[17] Bool, F. H.; Kist, J. R.; Locher, J. L.; and Wierda, F., M. C. Escher: His Life and Complete Graphic Work, New York: Harry N. Abrams, Inc.: p.323, 1992年9月1日, ISBN 9780810981133

[18] Arthur Loeb, "Polyhedra in the Work of M.C. Escher," in Coxeter et al. (eds.), M.C. Escher: Art and Science, 1986.

[19] George Hart. The Polyhedra of M.C. Escher. [2019-09-05]. （原始内容存档于2019-01-15）.

[20] Yoshimoto Cube No. 1 | MoMA Design Store. Museum of Modern Art Store. [20 August 2018]. （原始内容存档于2019-09-05）.

[etc.usf.edu_Hexakis_Octahedron-21] 19.0 ^19.1 Hexakis Octahedron. Florida Center for Instructional Technology, College of Education, University of South Florida. [2019-09-03]. （原始内容存档于2015-01-21）.

[22] Alan Holden, Shapes, Space and Symmetry, Columbia University Press, NY, 1971.

[article_beziau2003new-23] Béziau, Jean-Yves. New light on the square of oppositions and its nameless corner. Logical Investigations. 2003, 10 (2003): 218––232.

[article_moretti2010critics-24] Moretti, Alessio. The critics of paraconsistency and of many-valuedness and the geometry of oppositions. Logic and Logical Philosophy. 2010, 19 (1-2): 63––94.

[incollection_smessaert2015beziau-25] Smessaert, Hans and Demey, Lorenz, Béziau’s contributions to the logical geometry of modalities and quantifiers, The road to universal logic (Springer), 2015: 475––493

[coxeter-26] Coxeter, H. S. M., A special book review: M. C. Escher: His life and complete graphic work, The Mathematical Intelligencer, 1985, 7 (1): 59–69, doi:10.1007/BF03023010 Coxeter's analysis of Stars is on pp. 61–62.

[1]

[2]

[3]

[4]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[5]