開普勒定律
此條目需要補充更多來源。 (2015年7月26日) |

開普勒定律(英語:Kepler's law)是由德國天文學家、數學家約翰尼斯·克卜勒所發現的、關於行星運動的定律。開普勒於1609年在他出版的《新天文學》科學雜誌上發表了關於行星運動的兩條定律,又於1618年,發現了第三條定律。
開普勒幸運地得到了著名丹麥天文學家第谷·布拉赫所觀察與收集、且非常精確的天文資料。大約於1605年,根據布拉赫的行星位置資料,開普勒發現行星的移動遵守著三條相當簡單的定律。同年年底,他撰寫完成了發表文稿。但是,直到1609年,才在《新天文學》科學雜誌發表,這是因為布拉赫的觀察數據屬於他的繼承人,不能隨便讓別人使用,因此產生的一些法律糾紛造成了延遲。
在天文學與物理學上、開普勒的定律給予亞里士多德派與托勒密派極大的挑戰。他主張地球是不斷地移動的;行星軌道不是圓形(epicycle)的,而是橢圓形的;行星公轉的速度不等恆。這些論點,大大地動搖了當時的天文學與物理學。經過幾乎一個世紀的研究,物理學家終於能夠運用物理理論解釋原理。牛頓應用他的第二定律和萬有引力定律,在數學上嚴格地証明了開普勒定律,也讓人了解了其中的物理意義。
開普勒定律
[編輯]開普勒的三條行星運動定律改變了整個天文學,徹底摧毀了托勒密複雜的宇宙體系,完善並簡化了哥白尼的日心說。
開普勒第一定律
[編輯]
開普勒的第一定律,亦稱為橢圓定律、軌道定律:每一個行星都沿著各自的橢圓軌道環繞著太陽,而太陽則處在橢圓的一個焦點上。[1]
開普勒第二定律
[編輯]
開普勒第二定律,也稱為等面積定律:在相等時間內,太陽和運動着的行星的連線所掃過的面積都是相等的。[1]
這一定律實際揭示了行星繞太陽公轉的角動量守恆。用公式表示為
- 。
由此定律可以推知,行星離太陽較近時,運行速度較大,離太陽較遠時,運行速度較小。
開普勒第三定律
[編輯]
開普勒第三定律,也稱為週期定律:各個行星繞太陽公轉周期的平方及其橢圓軌道的半長軸的立方成正比。[1] 用公式表示為
- ;
其中是常量,它只與中心天體有關。
由這一定律導出:行星與太陽之間的引力與半徑的平方成反比。這是艾薩克·牛頓的萬有引力定律的一個重要基礎。
用公式表示為
- ;
這裡, 是行星公轉軌道半長軸, 是行星公轉周期, 是常數。
數學推導:由牛頓萬有引力定律導出開普勒定律
[編輯]開普勒定律描述的是行星圍繞太陽的運動,牛頓定律可以更廣義地描述幾個粒子因萬有引力相互吸引而形成的運動。假設只有兩個粒子,其中一個粒子超輕於另外一個粒子,則輕的粒子會繞著重的粒子運動,就好似行星根據開普勒定律繞著太陽運動。另外,牛頓定律還可計算出關於其它方面的解答,行星軌道可以呈拋物線運動或雙曲線運動。這是開普勒定律所無法預測到的結果。在一個粒子並不超輕於另外一個粒子的狀況下,依照廣義二體問題的解答,每一個粒子會繞著它們的共同質心運動。這也是開普勒定律無法預測到的。
開普勒定律使用幾何語言將行星的坐標及時間跟軌道參數相連結。牛頓第二定律是一個微分方程式。開普勒定律的推導涉及一些解析微分方程式的技巧。在推導開普勒第一定律之前,必須先推導出開普勒第二定律,因為開普勒第一定律需要用到開普勒第二定律裏的一些計算結果。
開普勒第二定律推導
[編輯]牛頓萬有引力定律表明,任意兩個粒子由通過連線方向的力相互吸引。該引力的大小與它們的質量乘積成正比,與它們距離的平方成反比。由於太陽超重於行星,可以假設太陽是固定的。用方程式表示,
- ;
這裏, 是太陽作用於行星的萬有引力, 是行星的質量, 是太陽的質量, 是行星相對於太陽的位移向量, 是 的單位向量。
牛頓第二定律表明,物體受力後所產生的加速度 ,和其所受的淨力 成正比,和其質量 成反比,以方程式表示,
- 。
合併這兩個方程式,
- 。 (1)
思考位置向量 ,對於時間 微分一次可得到速度向量,再微分一次則可得到加速度向量:
- ,
- 。(2)
在這裡,用到了單位向量微分方程式:
- ,
- 。
其中, 是向量 的極角, 是該向量逆時針旋轉 90 度的向量。
合併方程式 (1) 與 (2) ,可以得到向量運動方程式:
取各個分量,可以得到兩個常微分方程式,一個是關於徑向加速度,另一個是關於切向加速度:
- ,(3)
- 。(4)
導引開普勒第二定律只需切向加速度方程式。
試想行星的角動量 。由於行星的質量是常數,角動量對於時間的導數為
- 。
角動量 也是一個運動常數,即使距離 與角速度 都可能會隨時間變化。
在很小的時間 中,恆星與行星連線掃過的面積 近似於一個以 為底, 以 為高的三角形,故
從時間 到時間 掃過的區域 ,
- 。
行星太陽連線掃過的區域面積相依於間隔時間 。所以,開普勒第二定律是正確的。
開普勒第一定律推導
[編輯]設定 。這樣,角速度是
- 。
對時間微分和對角度微分有如下關係:
- 。
根據上述關係,徑向距離 對時間的導數為:
- 。
再求一次導數:
- 。
代入徑向運動方程式 (3) , ,
- 。
將此方程式除以 ,則可得到一個簡單的常係數非齊次線性全微分方程式來描述行星軌道:
- 。
為了解這個微分方程,先列出一個特解
- 。
再求解剩餘的常係數齊次線性全微分方程式,
- 。
它的解為
- ;
這裡, 與 是常數。合併特解和與齊次方程解,可以得到通解
- 。
選擇坐標軸,讓 。代回 ,
- ;
其中, 是離心率。
這是圓錐曲線的極坐標方程式,坐標系的原點是圓錐曲線的焦點之一。假若 ,則 所描述的是橢圓軌道。這證明了開普勒第一定律。
開普勒第三定律推導
[編輯]在建立牛頓萬有引力定律的概念與數學架構上,開普勒第三定律是牛頓依據的重要線索之一。假若接受牛頓運動定律。試想一個虛擬行星環繞着太陽公轉,行星的移動軌道恰巧呈圓形,軌道半徑為 。那麼,太陽作用於行星的萬有引力為 。行星移動速度為 。依照開普勒第三定律,這速度 與半徑的平方根 成反比。所以,萬有引力 。猜想這大概是牛頓發現萬有引力定律的思路,但這個猜想無法被證實,因為在他的計算本里,並沒有找到任何關於這方面的證據。
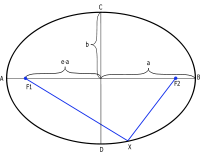
開普勒第一定律闡明,行星環繞太陽的軌道是橢圓形的。橢圓的面積是 ;這裡, 與 分別為橢圓的半長軸與半短軸。在開普勒第二定律推導里,行星-太陽連線掃過區域速度 為
- 。
所以,行星公轉周期 為
- 。(5)
關於此行星環繞太陽,橢圓的半長軸 ,半短軸 與近拱距 (近拱點 A 與引力中心之間的距離),遠拱距 (遠拱點 B 與引力中心之間的距離)的關係分別為
- ,(6)
- 。(7)
如果想要知道半長軸與半短軸,必須先求得近拱距與遠拱距。依據能量守恆定律,
- 。
在近拱點 A 與遠拱點 B,徑向速度都等於零:
- 。
所以,
- 。
稍微加以編排,可以得到 的一元二次方程式:
- 。
其兩個根分別為橢圓軌道的近拱距 與遠拱距 。
- ;
- 。
代入方程式 (6) 與 (7) ,
- ,
- 。
代入方程式 (5) ,周期的方程式為
- 。
參見
[編輯]參考資料
[編輯]
| ||||||||||
| ||||||



















































































