歐幾里得幾何
此條目沒有列出任何參考或來源。 (2016年9月5日) |

| 幾何學 |
|---|
 |
| 幾何學家 |
|
|
歐幾里得幾何有時就指二維平面上的幾何,即平面幾何,本文主要描述平面幾何。三維空間的歐幾里得幾何通常叫做立體幾何,高維的情形請參看歐幾里得空間。
數學上,歐幾里得幾何是二維平面和三維空間中的幾何,基於點線面公設。數學家也用這一術語表示具有相似性質的高維幾何。
其中公設五又稱之為平行公設(Parallel Axiom),敘述比較複雜,這個公設衍生出「三角形內角和等於一百八十度」的定理。在高斯(F. Gauss, 1777年—1855年)的時代,公設五就備受質疑,俄羅斯數學家羅巴切夫斯基(Nikolay Ivanovitch Lobachevski)、匈牙利數學家波約(Bolyai)闡明第五公設只是公理系統的一種可能選擇,並非必然的幾何真理,也就是「三角形內角和不一定等於一百八十度」,從而發現非歐幾里得的幾何學,即非歐幾何(non-Euclidean geometry)。
公理描述
[編輯]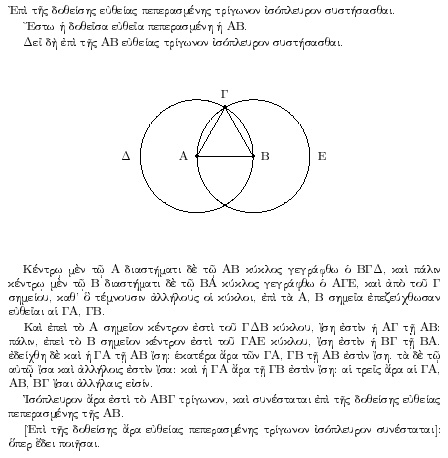
歐幾里得幾何的傳統描述是一個公理系統,通過有限的公理來證明所有的真命題。
歐幾里得平面幾何的五條公理(公設)是:
- 從一點向另一點可以引一條直線。
- 任意線段能無限延伸成一條直線。
- 給定任意線段,可以以其一個端點作為圓心,該線段作為半徑作一個圓。
- 所有直角都相等。
- 若兩條直線都與第三條直線相交,並且在同一邊的內角之和小於兩個直角,則這兩條直線在這一邊必定相交。
| “ | 通過一個不在直線上的點,有且僅有一條不與該直線相交的直線。 | ” |
平行公理並不像其他公理那麼顯然。許多幾何學家嘗試用其他公理來證明這條公理,但都沒有成功。19世紀,通過構造非歐幾里得幾何,說明平行公理是不能被證明的(若從上述公理體系中去掉平行公理,則可以得到更一般的幾何,即絕對幾何)。
從另一方面講,歐幾里得幾何的五條公理(公設)並不完備。例如,該幾何中的定理:在任意直線段上可作一等邊三角形。他用通常的方法進行構造:以線段為半徑,分別以線段的兩個端點為圓心作圓,將兩個圓的交點作為三角形的第三個頂點。然而,他的公理並不保證這兩個圓必定相交。[來源請求]因此,許多公理系統的修訂版本被提出,其中有希爾伯特公理。
歐幾里得還提出了五個一般概念,也可以作為公理。當然,之後他還使用量的其他性質。
- 與同一事物相等的事物相等。
- 相等的事物加上相等的事物仍然相等。
- 相等的事物減去相等的事物仍然相等。
- 一個事物與另一事物重合,則它們相等。
- 整體大於局部。
現代方法
[編輯]如今,歐幾里得幾何的構造通常不是通過公理化方法,而是通過解析幾何。通過這種方法,可以像證明定理一樣證明歐幾里得幾何(或非歐幾里得幾何)中的公理。這一方法沒有公理方法那麼漂亮,但絕對簡練。
- 構造
首先,定義點的集合為實數對的集合。給定兩個點和,定義距離:
- .
這就是歐幾里得度量。所有其他概念,如直線、角、圓可以通過作為實數對的點和之間的距離來定義。例如通過點和的直線可以定義成點的集合滿足
- 或。
經典定理
[編輯]參見
[編輯]
| ||||||||||||||||||||||||||||||||||
|










