複振器

複振器是一種用來產生在兩種狀態間變化的系統的電子電路，譬如說振盪器、計數器、flip-flop等等。最常見的形式是用來產生方波的非穩態振盪器。

複振器大致上可以分成3種：

• 非穩態複振器 (astable multivibrator), 這種電路不管在哪一種狀態中都不是穩定的；它持續的由一種狀態轉變到另一種狀態，這種複振器又被稱為弛張振盪器。

• 單穩態複振器 (monostable multivibrator), 它所處的兩種狀態中有一種是穩態。這種電路會在外部訊號觸發時落入非穩態，但是在非穩態持續一段時間後還是會回到穩態。這種電路適用於對外部事件產生持續固定長度的訊號，也有人稱這一類的電路叫单稳态触发器（One Shot）電路，常見於用來除去Switch Bounce的現象。

Bistable multivibrator (R1, R2 = 1 kΩ, R3, R4 = 10 kΩ).

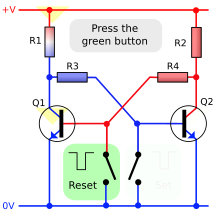
• 雙穩態複振器 (bistable multivibrator), 這種電路的兩種狀態都是穩態。如果沒有特定訊號觸發的話，它會一直處在其中一種狀態。若是有特定訊號觸發，此電路可以由一種狀態轉變到另一種狀態。它可以在建立基礎的記憶元件，如電腦中的記憶體或是中央處理器內部的暫存器。此電路也被稱為触发器或锁存器。有一種類似的電路是施密特触发器。

最簡單的複振器是由兩個交互偶合的電晶體構成的，並在電路中使用不同的RC電路以決定處於不同狀態的時間。

複振器常見於需要產生方波或定寬時脈的系統中，不過簡單的電路也意味著不夠精確的時脈控制，因此在時間因素非常重要的系統中較少見到複振器。

555計時IC是一種廣泛使用的積體電路版本的複振器。555計時IC中使用了更精密的設計以解決一般複振器定時不準的問題。

非穩態複振器電路

上圖說明了典型非穩態複振器電路的組態。

基本操作模式

此電路運作在以下兩種狀態：

狀態一

• Q1導通
• Q1的集極電壓為接近0V
• C1由流經R2及Q1的電流充電
• Q2基極的電壓等於C1兩端跨壓，此電壓將隨著C1充電的過程持續上升(尚未達到0.6V）
• Q2截止（假設Q2的基極電壓小於0.6V）
• C2經由R3及R4放電
• 輸出電壓為高（但因C2經由R4放電的緣故，較電源電壓稍低）
• 此狀態一直持續到Q2的基極電壓達到0.6V以前。當Q2基極電壓達0.6V時，Q2導通：此電路進入狀態二

狀態二

• Q2導通
• Q2的集極電壓（即是輸出電壓）由高電位變為接近0V
• C2把Q2集極電壓變化偶合到Q1的基極，使Q1瞬間截止
• Q1截止，使得Q1集極電壓上升到高電位
• C1經由R1及R2放電
• C2從低電位利用流經R3的電流充電，使C2由0V漸漸充電至0.6V
• 因Q1的基極電壓等於C2兩端跨壓，所以隨著C2充電，Q1的基極電壓也漸漸升高
• 此狀態一直持續到Q1的基極電壓達到0.6V以前。當Q1基極電壓達0.6時，Q1導通：此電路進入狀態一

電路啟動過程

當電路剛接上電源時，兩個電晶體都是截止狀態。不過，當這兩個電晶體的基極電壓一起上升時，由於電晶體製造過程中不可能把每個電晶體的導通延时控制得一樣，所以必然有其中一個電晶體搶先導通。於是此電路便進入其中一種狀態，而且也保証可以持續振盪。

振盪週期

粗略的來說，狀態一（輸出高電位）的持續時間與R1、C1相關，狀態二的持續時間與R2、C2相關。因為R1、R2、C1、C2都可以自由配置，因此可以自由決定振壓週期及duty cycle。

不過，在每個狀態的持續時間是由電容在充電開始時的初始狀態（電容兩端的電壓）決定的，而這又與前一個狀態中的放電量有關；前一個階段的放電量又由放電過程中電流通過的電阻R1、R4與放電過程的持續時間決定…。總而言之，在剛啟動電路時，要花費頗長的時間把電容充電（一般而言電容兩端在未啟動時是完全放電的），不過之後的各個階段的持續時間便會變短並趨於穩定。

因為複振器是利用電流的充電過程控制週期，所以振盪週期同時也與輸出端流出複振器的電流量有關。

由於種種不隱定因素對複振器振盪週期的影響，因此在實作中通常使用更精確的計時積體電路取代單純的複振器電路。

單穩態複振器

雙穩態複振器

外部連結

• Java applets 模擬複振器運作