边收缩

在图论中,边收缩是指將一個圖的其中一個邊移除,並將被移除邊的兩個頂點合併,同時保持與被移除邊之頂點相連的其他頂點之連接關係的一種變換,為圖子式理論中的基本運算元之一,然而此種變換不一定是圖論中的變換,亦可以作用於拓樸結構甚至是幾何體,例如邊收縮二十面體,即正二十面體經過一次邊收縮變換後的像。另一種與邊收縮類似的圖論變換為點合併(vertex contraction)是邊收縮變換的一個廣義形式。
定义
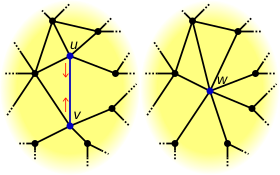
[编辑]邊收縮是一種作用於邊上的變換,因此其需作用於特定的邊,令其計為e,並令e所連接的兩個頂點計為u和v,而邊收縮會使頂點u和v合併成一個新的頂點w,並使原本與u和v相連的所有邊都連到w。通常一系列的邊進行邊收縮變換的先後順序不會影響結果,換句話說即邊收縮是一個具有交換律的變換[2]。
邊收縮變換有時會計為 G / e,類似於 G \ e,但 G \ e 指的是完全將e從G中移除。
根據下述的幾個定義,邊收縮可能會導致多重邊的形成,也就是產生了有至少二個邊的二個頂點完全相同、至少有二個頂點可以由二個邊相連接的圖,即使原本的圖是一個簡單圖,也可能導致變換結果為伪图[4]。
正式定義
[编辑]令G=(V,E)是一個圖,亦可以是有向圖或無向圖,並令e=(u,v)是圖G中的其中一個邊,且u≠v。 定義f是一個圖論變換函數,其可以將除了{u,v}外的所有頂點(V\{u,v})映射(或變換)到本身,其餘情況則映射到新頂點w。而針對e的邊收縮變換函數其變換後的像可以表示為:
- G′=(V′,E′)
其中V′為除了{u,v}外的所有頂點與{w}的聯集(V′=(V\{u,v})∪{w})、E′為除了e之外的所有邊(E′=E\{e})。對所有的x∈V,x′=f(x)∈V′,若邊e∈E與x相連則邊e′∈E′與x′相連,反之亦然。
用途
[编辑]邊收縮或點合併可以用於圖論的數學歸納法,尤其是對於使用圖之邊或頂點個數的數學歸納法很有幫助,因為我們可以透過先假設某特性在所有較小的圖皆成立,並透過將該特性推導到較大的圖來證明。
相關變換
[编辑]點合併
[编辑]點合併 (Vertex identification)是指將兩個不一定落在同一條邊上的頂點合併成一個頂點,並將原本與舊頂點相連的頂點改連接到這個合併而成的新頂點。
簡化
[编辑]簡化,又稱為平滑(smoothing),是邊收縮的一個特例,當邊收縮選定的邊其中一個頂點的度為2,則該變換又可稱為簡化(或平滑)。其逆變換稱為細分。
當一個圖套用平滑變換之後,其所產生的新圖會與原圖同胚。
幾何形狀的邊收縮
[编辑]當一個幾何形狀是具有點可遞性質時,我們可以對該多面體進行邊收縮變換,其變換結果至少會少一條邊,且必定會少一個頂點,而面和邊數量的變化則要看所選的邊是哪一種多邊形的邊,例如三角形面會消失,若邊重合則會再多減少一條邊。例如正二十面體套用邊收縮變換之後少掉了2個三角形面、少掉了3條邊(2個三角形退化成邊並與原有邊重合因此被移除)和一個頂點。
 正二十面體 |
 邊收縮二十面體 |
参见
[编辑]參考文獻
[编辑]- ^ Gross, Jonathan; Yellen, Jay, Graph Theory and its applications, CRC Press, 1998, ISBN 0-8493-3982-0
- ^ Gross & Yellen 1998[1], p. 264
- ^ Rosen, Kenneth, Discrete Mathematics and Its Applications 7th, McGraw-Hill, 2011, ISBN 9780073383095
- ^ Rosen 2011[3], p. 664
- Oxley, James, Matroid Theory, Oxford University Press, 1992
- West, Douglas B., Introduction to Graph Theory 2nd, Prentice-Hall, 2001, ISBN 0-13-014400-2
