德勞內三角剖分
外观
(重定向自德勞內三角化)

在數學和計算幾何領域,平面上的點集P的德勞內三角剖分(英語:Delaunay triangulation)是一種是点P的一个三角剖分DT,使在P中沒有點嚴格處於 DT(P) 中任意一個三角形外接圓的內部。德勞內三角剖分最大化了此三角剖分中三角形的最小角,換句話,此算法儘量避免出現「極瘦」的三角形。此算法命名來源於鮑里斯·德勞內,以紀念他自1934年在此領域的工作。[1]
與沃羅諾伊圖的關係
[编辑]若一離散點集的點均處於一般位置,則德勞內三角化就對應到沃罗诺伊图的對偶。特殊情形包括了三點共線及四點共圓
-
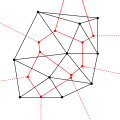
一個德勞內三角化的例子,所有三角形外接圓的圓心以紅點表示。
-
連接外接圓圓心即產生沃罗诺伊图,在此以紅線表示。
參見
[编辑]- ^ B. Delaunay: Sur la sphère vide, Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7:793–800, 1934