偏三角面體
 以六方偏三角面體(或稱複三方偏三角面體)為例 | |
| 類別 | 偏三角面體 |
|---|---|
| 性質 | |
| 面 | |
| 邊 | |
| 頂點 | |
| 歐拉特徵數 | F=, E=, V= (χ=2) |
| 組成與佈局 | |
| 面的種類 | 2n個不等邊三角形 |
| 對稱性 | |
| 對稱群 | Dnd, [2+,2n], (2*n), order 4n |
| 旋轉對稱群 | Dn, [2,n]+, (22n), order 2n |
| 特性 | |
| 凸、面可遞 | |
| 註:為底面邊數 。 | |
偏三角面體(scalenohedron)[1] 是指由作為底的鋸齒扭歪多邊形之頂點與其中心正上方及正下方的兩對稱頂點相連所形成的立體。 在礦物學中,偏三角面體指上述形狀的晶形[2],也就是說部分礦物的晶形為偏三角面體,例如方解石[3]。
偏三角面體通常以底的邊數命名,例如底為六邊形的偏三角面體稱為六方偏三角面體(hexagonal scalenohedron),由上下各6個共12個不等邊三角形組成[4]:245。 而部分偏三角面體以複偏三角面體的方式存在,即對稱性為n邊形二面體群的複偏三角面體其底為鋸齒扭歪2n邊形,這種立體通常命名為複n角偏三角面體或複n方偏三角面體(di-n-gonal scalenohedron)。 在晶體學中,亦有複偏三角面體的晶形,尤其以複二方(didigonal,8個面)和複三方(ditrigonal,12個面)最為常見。[5][6]
偏三角面體所有面都是全等的不等邊三角形,且其為等面圖形。其可以視為一種直「對稱」的、擁有鋸齒扭歪多邊形之底的雙錐體,也可以視為將每個四邊形面各分割成兩個不等邊三角形的偏方面體。
性質
[编辑]n方偏三角面體由上下兩個頂點、n個底面頂點、2n個面和3n條邊組成;而複n方偏三角面體由上下兩個頂點、2n個底面頂點、4n個面和6n條邊組成;其拓樸結構等價於雙2n角錐,但其2n邊形的頂點位於兩個環上,一個在幾何中心之上方、另一個在幾何中心之下方。[5]
「正」直「對稱」的複n方偏三角面體(或稱複n角偏三角面體)有n個過相對底邊中點的兩倍旋轉對稱軸、n個過相對頂邊的鏡射對稱平面、1個過上下兩頂點的n倍旋轉對稱軸和1個過上下兩頂點的2n倍旋轉反射對稱軸(圍繞這個軸做1n次瑕旋轉立體保持原樣)[6],對應的對稱群為Dnv = Dnd, [2+,2n], (2*n),其階數為4n階(如果n為奇數,則存在關於中心的点反演對稱性,對應於180°的旋轉反射)。
以2n = 2×3為例:
- 「正」直「對稱」的複三方偏三角面體具有3個類似的垂直對稱平面,彼此傾斜60°並相交於鉛直的3倍旋轉對稱軸、3個類似的水平2倍旋轉對稱軸,每個水平2倍旋轉對稱軸垂直於對稱面、点反演對稱中心[7]:577,599和鉛直的6倍旋轉反射對稱軸。
例子
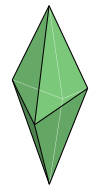
[编辑]| 複二方偏三角面體 正方偏三角面體 四方偏三角面體 |
複三方偏三角面體 六方偏三角面體 |
複四方偏三角面體 八方偏三角面體 |
複五方偏三角面體 十方偏三角面體 |
複六方偏三角面體 十二方偏三角面體 |
|---|---|---|---|---|
|

|

|

|

|
參見
[编辑]參考文獻
[编辑]- ^ 偏三角面體 scalenohedron. 樂詞網, 國家教育研究院. [2023-01-08]. (原始内容存档于2023-01-09).
- ^ skalenoeder. norske leksikon. 2009-02-14 [2023-01-10]. (原始内容存档于2023-01-10).
- ^ 方解石. catalog.digitalarchives.tw. [2023-01-08]. (原始内容存档于2023-01-09).
- ^ 臺灣商務印書館. 編審委員會. 增修辭源, 第 1 卷. 增修辭源. 臺灣商務印書館. 1979 [2023-01-08]. ISBN 9789570513738. (原始内容存档于2023-01-08).
- ^ 5.0 5.1 The 48 Special Crystal Forms. 2013-09-18 [2020-11-18]. (原始内容存档于2013-09-18).
- ^ 6.0 6.1 Crystal Form, Zones, Crystal Habit. Tulane.edu. [2017-09-16]. (原始内容存档于2013-09-01).
- ^ Spencer, Leonard James. Crystallography. Chisholm, Hugh (编). Encyclopædia Britannica 07 (第11版). London: Cambridge University Press: 569–591. 1911.




