傅科擺 鐘擺原理 擺 是一種實驗儀器,可用來展現種種力學現象。最基本的擺由一條繩 或竿,和一個錘組成。錘繫在繩的下方,繩的另一端固定。當推動擺時,錘來回移動。擺可以作一個計時器。
若最高處(
v
=
0
{\displaystyle v=0}
θ
{\displaystyle \theta }
θ
≤
5
∘
{\displaystyle \theta \leq 5^{\circ }}
則可使用下列公式算出它的振動週期 。
T
=
2
π
L
g
{\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}}
L
{\displaystyle L}
g
{\displaystyle g}
一擺長為
1
{\displaystyle 1}
簡諧運動 ,週期
T
≈
2.0
s
{\displaystyle T\approx 2.0s}
秒擺 。
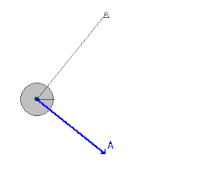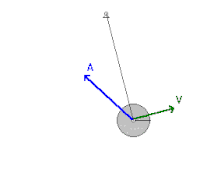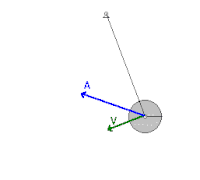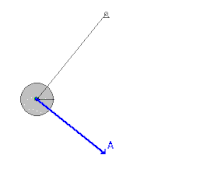
一單擺擺錘正在擺盪最高處(此時
v
=
0
{\displaystyle v=0}
θ
{\displaystyle \theta }
L
{\displaystyle L}
x
{\displaystyle x}
此物體受下列力的影響(下列說明錯誤,繩子的張力是因為擺錘重力引起,任何一瞬間擺錘法向(徑向)合力為零,但切線加速度為
−
g
sin
θ
{\displaystyle -g\sin \theta }
繩子之拉力大小
F
{\displaystyle F}
重力大小
F
g
=
m
g
{\displaystyle F_{g}=mg}
繩子的拉力
F
{\displaystyle F}
F
cos
θ
=
m
g
{\displaystyle F\cos \theta =mg}
F
sin
θ
=
k
x
{\displaystyle F\sin \theta =kx}
∵
lim
θ
→
0
cos
θ
=
1
{\displaystyle \because {\underset {\theta \to 0}{\mathop {\lim } }}\,\cos \theta =1}
∴
F
≈
m
G
g
{\displaystyle \therefore F\approx m_{G}g}
F
sin
θ
=
m
G
g
(
x
L
)
=
k
x
{\displaystyle F\sin {\theta }=m_{G}g\left({\frac {x}{L}}\right)=kx}
k
=
m
G
g
L
{\displaystyle k={\frac {m_{G}g}{L}}}
代入
T
=
2
π
m
I
k
{\displaystyle T=2\pi {\sqrt {\frac {m_{I}}{k}}}}
得到
T
=
2
π
m
I
L
m
G
g
{\displaystyle T=2\pi {\sqrt {\frac {m_{I}L}{m_{G}g}}}}
根據廣義相對論 可知,
m
I
=
m
G
{\displaystyle m_{I}=m_{G}\,}
故
T
=
2
π
L
g
{\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}}
sin θ 取為θ的誤差。 「
单摆 」重定向至此。
取
L
{\displaystyle L}
θ
{\displaystyle \theta }
θ
0
{\displaystyle \theta _{0}}
θ
{\displaystyle \theta }
m
{\displaystyle m}
θ
¨
{\displaystyle {\ddot {\theta }}}
α
=
d
2
θ
d
t
2
{\displaystyle \alpha ={\frac {{\rm {d}}^{2}\theta }{{\rm {d}}t^{2}}}}
忽略空氣阻力以及繩的彈性、重量的影響:
錘速率最高是在
θ
=
0
{\displaystyle \theta =0}
運動方程為:
m
L
θ
¨
=
−
m
g
sin
θ
{\displaystyle mL{\ddot {\theta }}=-m{\rm {g}}\sin \theta }
注意到不論θ 的值為何,運動週期和錘的質量無關。
當
θ
{\displaystyle \theta }
sin
θ
≈
θ
{\displaystyle \sin \theta \approx \theta }
簡諧運動 ,週期
T
=
2
π
L
g
{\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}}
準確的運動週期不可以用基礎函數求得。考慮微分方程:
d
t
d
θ
=
1
2
L
g
1
cos
θ
−
cos
θ
0
{\displaystyle {{\rm {d}}t \over {\rm {d}}\theta }={1 \over {\sqrt {2}}}{\sqrt {L \over {\rm {g}}}}{1 \over {\sqrt {\cos \theta -\cos \theta _{0}}}}}
T
=
θ
0
→
0
→
−
θ
0
→
0
→
θ
0
=
4
(
θ
0
→
0
)
{\displaystyle T=\theta _{0}\rightarrow 0\rightarrow -\theta _{0}\rightarrow 0\rightarrow \theta _{0}=4\left(\theta _{0}\rightarrow 0\right)}
T
=
4
1
2
L
g
∫
0
θ
0
1
cos
θ
−
cos
θ
0
d
θ
{\displaystyle T=4{1 \over {\sqrt {2}}}{\sqrt {L \over {\rm {g}}}}\int _{0}^{\theta _{0}}{1 \over {\sqrt {\cos \theta -\cos \theta _{0}}}}\,{\rm {d}}\theta }
將上式重寫成第一類橢圓函數 的形式:
T
=
4
L
g
F
(
sin
θ
0
2
,
π
2
)
{\displaystyle T=4{\sqrt {L \over {\rm {g}}}}F\left({\sin {\theta _{0} \over 2}},{\pi \over 2}\right)}
其中
F
(
k
,
ϕ
)
=
∫
0
ϕ
1
1
−
k
2
sin
2
θ
d
θ
.
{\displaystyle F(k,\phi )=\int _{0}^{\phi }{1 \over {\sqrt {1-k^{2}\sin ^{2}{\theta }}}}\,{\rm {d}}\theta .}
週期可以用級數表示成:
T
=
2
π
L
g
[
1
+
(
1
2
)
2
sin
2
θ
0
2
+
(
1
⋅
3
2
⋅
4
)
2
sin
4
θ
0
2
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
2
sin
6
θ
0
2
+
⋯
]
{\displaystyle T=2\pi {\sqrt {L \over {\mathrm {g} }}}\left[1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}\sin ^{6}{\frac {\theta _{0}}{2}}+\cdots \right]}
=
2
π
L
g
(
1
+
1
16
θ
0
2
+
11
3072
θ
0
4
+
⋯
)
=
2
π
L
g
[
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
2
sin
2
n
(
θ
0
2
)
]
{\displaystyle =2\pi {\sqrt {\frac {L}{g}}}\left(1+{\frac {1}{16}}\theta _{0}^{2}+{\frac {11}{3072}}\theta _{0}^{4}+\cdots \right)=2\pi {\sqrt {\frac {L}{g}}}\left[\sum _{n=0}^{\infty }\left({\frac {\left(2n\right)!}{2^{2n}\left(n!\right)^{2}}}\right)^{2}\sin ^{2n}\left({\frac {\theta _{0}}{2}}\right)\right]}
衝擊擺是來用計算子弹速度的實驗室儀器。它的原理為:物件碰撞前後動量守恒 ,擺運動時能量守恒 。
衝擊擺和普通擺相似,特別之處它的錘會和射入子弹產生完全非彈性碰撞,即碰撞後兩者會合為一。
將子弹射向停止的錘,使錘和子弹合在一起擺動。設錘質量為
m
p
{\displaystyle m_{p}\,}
m
b
{\displaystyle m_{b}\,}
v ,錘和子弹碰撞後的速度為u 。
以下是子弹速度的計算方法:
由動量守恒定律 ,
m
b
×
v
+
m
p
×
0
=
(
m
b
+
m
p
)
×
u
{\displaystyle m_{b}\times v+m_{p}\times 0=(m_{b}+m_{p})\times u}
由能量守恒定律 ,
1
2
(
m
b
+
m
p
)
u
2
=
(
m
b
+
m
p
)
g
h
{\displaystyle {\frac {1}{2}}(m_{b}+m_{p})u^{2}=(m_{b}+m_{p})gh}
解得
v
=
(
m
b
+
m
p
)
2
g
h
m
b
{\displaystyle v={\frac {(m_{b}+m_{p}){\sqrt {2gh}}}{m_{b}}}}
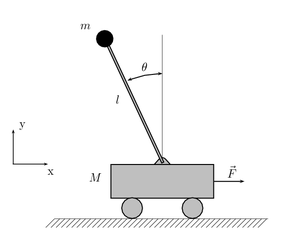
和台車和倒單擺組成的系統 倒單擺有許多不同的架構,常見的有二種。
最簡單的是無質量的直桿一端接在固定的樞紐上,另一端連結重量,此架構類似一般單擺,但因為重量在樞紐點上方,直桿在重量下方,需支持重物不落下,因此會將單擺的線改為有剛性的直桿。
另外一種是將倒單擺放在可以一維水平運動的台車上,透過台車的水平運動來控制擺的位置。
倒單擺在擺直立朝上時可以平衡,不過是不穩定平衡,需要透過控制系統才能維持平衡。
圓錐 面。這是圓周運動 。
[ 编辑 ] 「
复摆 」重定向至此。
當質量不集中或不規則的物體以轉軸吊起擺動時,此擺稱作複擺(物理擺)。由於有質量分佈的緣故,週期跟剛性物體重心對轉軸的轉動慣量(I)有關。根據平行軸定理及可以求出小角度複擺週期為
T
=
2
π
I
m
g
d
{\displaystyle T=2\pi {\sqrt {\frac {I}{mgd}}}}
[ 编辑 ] 雙擺系統的一例 雙擺系統是混沌的。
和雙擺一樣,磁性擺系統是混沌的。
傅科擺的移動可作為地球自轉的證據。
擺鐘。
為了減少溫度變化的影響,有不同的設計:
柵形補償擺(Gridiron Pendulum):以不同金屬(鋼和銅)配搭,保持擺的長度不變[ 1]
Graham's pendulum:有一個水銀管柱,保持擺的重心不變
以木製擺[ 2]
Ellicott compensated pendulum:用多個擺的結構配合 Paul Appell, "Sur une interprétation des valeurs imaginaires du temps en Mécanique", Comptes Rendus Hebdomadaires des Scéances de l'Académie des Sciences, volume 87, number 1, July, 1878.
The Pendulum: A Physics Case Study, Gregory L. Baker and James A. Blackburn, Oxford University Press, 2005
^ [1] (页面存档备份 ,存于互联网档案馆 )^ [2] (页面存档备份 ,存于互联网档案馆 )







































![{\displaystyle T=2\pi {\sqrt {L \over {\mathrm {g} }}}\left[1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}\sin ^{6}{\frac {\theta _{0}}{2}}+\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89530b6d177974d59c72066989d56d5a339d1442)
![{\displaystyle =2\pi {\sqrt {\frac {L}{g}}}\left(1+{\frac {1}{16}}\theta _{0}^{2}+{\frac {11}{3072}}\theta _{0}^{4}+\cdots \right)=2\pi {\sqrt {\frac {L}{g}}}\left[\sum _{n=0}^{\infty }\left({\frac {\left(2n\right)!}{2^{2n}\left(n!\right)^{2}}}\right)^{2}\sin ^{2n}\left({\frac {\theta _{0}}{2}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bc6b231c69b842d48ad60dc442655ae5e41603d)





