动态光散射
动态光散射,也称作光子相关光谱或准弹性光散射,是一种物理表征手段,用来测量溶液或悬浮液中的粒徑分布,[1]也可以用来测如量高分子浓溶液等的复杂流体的行为。
原理[编辑]
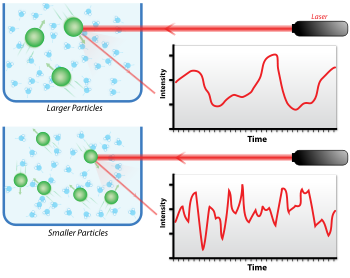
当光射到遠小于其波長的小颗粒上时,光会向各方向散射(瑞利散射)。如果光源是雷射,在某一方向上,我们可以观察到散射光的强度随时间而波动,这是因为溶液中的微小颗粒在做布朗运动,且每个发生散射的颗粒之间的距离一直随时间变化。來自不同顆粒的散射光因相位不同產生建設性或破壞性干涉。所得到的强度随时间波动的曲线带有引起散射的颗粒随时间移动的資訊。動態光散射實驗易受灰塵或雜質影響,故样品的过滤和离心十分重要。
颗粒的運動資訊可通过实验中记录到的散射光强度的自相关函數导出,二阶自相关曲函數的推导如下:
此处的是選定的波向量的自相关函数,是延迟时间,是散射光的强度。当延迟时间较短时,相关性较高,因为颗粒的移動距离短。故相差很短时间的两个訊号没有顯著差别。当延迟时间較长时,相关性呈指数衰减趋势,意味着经历较长时间后,两組訊号的散射光强度没有相关性。这一指数衰减的快慢和颗粒的运动特性关系密切,特别取决于扩散系数。基于假设分布的数学方法被用于与相关性相拟合。如果样品是单分散的,衰减是简单的指数关系。Siegert公式将二阶自我相关函数和一阶自我相关函数联系起来:
此处的参数β是取决于颗粒的集合形状的校正系数。它约等于speckles数目的反比。当激光束聚焦在较小的区域上时,会导致较粗糙的speckle pattern,探测器收集到较少的speckle,形成较大的二阶自相关函数。
多分散指数(Polydiseperse Index,PDI),即相对偏差(Relative variance),是指示分散度的重要指标,PDI = sigma2/ZD2,其中sigma是标准偏差,Z是Z平均尺寸。分散度(Polydispersity,Pd),是标准偏差(Standard deviation)、宽度(width)、绝对分散试(absolute polydispersity),或百分分散度(Polydispersity,%Pd)也就是偏差因子(Coefficient of variation)。其中%Pd = (PdI)1/2 × 100,也称作相对分散度。[2]
应用[编辑]
动态光散射用于表征蛋白质、高分子、胶束、糖和纳米颗粒的尺寸。如果系统是单分散的,颗粒的平均有效直径可以求出来,这一测量取决于颗粒的心,表面结构,颗粒的浓度和介质中的离子种类。DLS也可以用于稳定性研究,通过测量不同时间的粒径分布,可以展现颗粒随时间聚沉的趋势。随着微粒的聚沉,具有较大粒径的颗粒变多。同样,DLS也可以用来分析温度对稳定性的影响。
推荐书籍[编辑]
《激光光散射谱学》张明生著 科学出版社, 2008.5 《Laser light scattering》Chu, Benjamin著.New York, Academic Press, 1974.
参考资料[编辑]
- ^ Berne, B.J.; Pecora, R. Dynamic Light Scattering; Wiley: New York, 1976
- ^ "Dynamic light scattering and application to proteins in solutions"http://mafija.fmf.uni-lj.si/seminar/files/2009_2010/Dynamic_light_scattering_and_application_to_proteins_in_solutions.pdf (页面存档备份,存于互联网档案馆)







![{\displaystyle g^{2}(q;\tau )=1+\beta \left[g^{1}(q;\tau )\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec3b1e787d6c8072a7b9291b748854e4899c7ab1)