井字棋
 |
此条目没有列出任何参考或来源。（2010年9月21日） 維基百科所有的內容都應該可供查證。 请协助添加来自可靠来源的引用以改善这篇条目。无法查证的内容可能被提出异议而移除。 |
井字棋，大陸、台灣又稱為井字游戏、圈圈叉叉；另外也有打井遊戲、OX棋的稱呼，香港多稱井字過三關、过三关，是種纸笔游戏。
目录 |
[编辑] 玩法
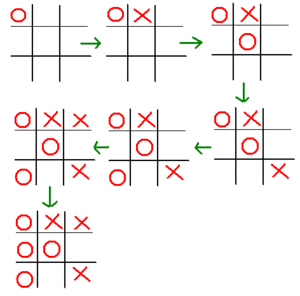
两个玩家，一個打圈(O)，一個打叉(X)，轮流在3乘3的格上打自己的符号，最先以横、直、斜连成一线则为胜。
如果雙方都下得正確無誤，將得和局。
这种游戏实际上是由第一位玩家所控制，第一位玩家是攻，第二位玩家是守。
第一位玩家在角位行第一子的话赢面最大（见图一），第二位玩家若是在邊位下子，第一位玩家就可以以两粒连线牵制著第二位玩家，然后制造「两头蛇」。
[编辑] 變化
因為原本的遊戲如果下法無誤，將得和局，所以出現變化，玩法是在下完第六子時(後方第三子)，最初的第一子要消失，第七子下完第二子消失，以此類推，保持盤上只有六子，下子後必須先處理消失之子，方可判斷是否連成一條線，這種玩法普通在紙上玩時，通常不用圈叉，多以不同顏色數字來表示(不然難以分辨何子先下，但是高手可以不用數字)，不過後來各類翻譯機都內建此遊戲，就都以圈叉表示了，此種玩法難度增高，先下者如下在邊則必勝，如下在別的地方，一樣正確進行會和局，但是由於變化複雜，多數人難以計算此變化，容易下錯，增加遊戲娛樂性。
[编辑] 人工智能
这种游戏的变化简单，常成为博弈论和遊戲樹搜寻的教学例子。这个游戏只有765个可能局面，26830个棋局。如果将对称的棋局视作不同，则有255168个棋局。
由于这种游戏的结构简单，早期这游戏就成为了人工智能的一个好题目。学生都要从既有的玩法中，归纳出游戏的致胜之道，并将策略演绎成为程式，让电脑与用户对弈。
世界上第一个电脑游戏，1952年为EDSAC电脑制作的OXO游戏，就是以该游戏为题材，可以正确无误地与人类对手下棋。
[编辑] 變種
[编辑] 立體井字棋
由原來的平面過三關，改變成為立體的 3x3x3 過三關。不過趣味不高，因為只要先手下在立方體中央就保證必勝。
