十五平均律
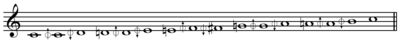


在音樂中,十五平均律(又稱15-TET、15-EDO或15-ET)是把一個八度平分為十五音級的平均律。每一級的頻率比率都是1:21/15,或80音分(ⓘ)。由於15是3乘5,所以十五平均律的音階可以分為三等分,每一等分都和印尼的甘美蘭的Slendro音階相似。十五平均律不是一個中庸全音律。
用途[编辑]
十五平均律的結他已經被製造了。美國音樂家温蒂·卡洛斯使用了十五平均律作為音欒專輯Tales of Heaven and Hell裏的曲目Afterlife的其中一個音階[3]。小伊斯利·布萊克伍德曾經替十五平均律的結他寫過一套組曲,並且替它錄了音[4]。他認為十五平均律「能通過很多種風格使古典音樂和流行音樂更豐富[5]」。
音程音距[编辑]
以下是十五平均率的常用音程的音距:
| 音程 | 音距(音級) | 音距(音分) | 純率(比率) | 純率(音分) | 誤差 | 音頻 |
|---|---|---|---|---|---|---|
| 完全五度 | 9 | 720 | 3:2 | 701.96 | +18.04 | ⓘ |
| 含七三全音 | 7 | 560 | 7:5 | 582.51 | −22.51 | ⓘ |
| 11:8寛四度 | 7 | 560 | 11:8 | 551.32 | +8.68 | ⓘ |
| 15:11寛四度 | 7 | 560 | 15:11 | 536.95 | +23.05 | ⓘ |
| 完全四度 | 6 | 480 | 4:3 | 498.04 | −18.04 | ⓘ |
| 含七大三度 | 5 | 400 | 9:7 | 435.08 | −35.08 | ⓘ |
| 含十一大三度 | 5 | 400 | 14:11 | 417.51 | −17.51 | ⓘ |
| 大三度 | 5 | 400 | 5:4 | 386.31 | +13.69 | ⓘ |
| 小三度 | 4 | 320 | 6:5 | 315.64 | +4.36 | ⓘ |
| 含七小三度 | 3 | 240 | 7:6 | 266.87 | −26.87 | ⓘ |
| 含七全音 | 3 | 240 | 8:7 | 231.17 | +8.83 | ⓘ |
| 大全音 | 3 | 240 | 9:8 | 203.91 | +36.09 | ⓘ |
| 小全音 | 2 | 160 | 10:9 | 182.40 | −22.40 | ⓘ |
| 大含十一自然二度 | 2 | 160 | 11:10 | 165.00 | −5.00 | ⓘ |
| 小含十一自然二度 | 2 | 160 | 12:11 | 150.63 | +9.36 | ⓘ |
| 純全音階半度 | 1 | 80 | 16:15 | 111.73 | −31.73 | ⓘ |
| 含七半音階半度 | 1 | 80 | 21:20 | 84.46 | −4.47 | ⓘ |
| 純半音階半度 | 1 | 80 | 25:24 | 70.67 | +9.33 | ⓘ |
第七個和第十一個諧波也能在十五平均律中找到,但第三個和第五個諧波在第十五平均率中只能找到差不多的音程。在十五平均律中的完全五度比在十二平均律、十九平均律和二十二平均律中的完全五度走調。在十五平均律中的大三度和在十二平均律中的大三度相同,但其他在兩個平均律中相同的音程比較不走調。十五平均律是包含第十一個諧波和一個可使用的完全五度的平均律中最小的一個,但是二十二平均率中有一個較好的第十一個諧波,而且有較多不走調的五度和大三度。
雖然十五平均律中也有完全五度、大和小三度,但是十五平均律和十二平均律中的完全五度、大和小三度帶給人的感覺較不同。十五平均律中有11:8和16:11的音程,但是十二平均律和十九平均律中都沒有。除此之外,十五平均律也有一個自然二度和含七全音。
參考資料[编辑]
- ^ Myles Leigh Skinner (2007). Toward a Quarter-tone Syntax: Analyses of Selected Works by Blackwood, Haba, Ives, and Wyschnegradsky, p.52. ISBN 9780542998478.
- ^ Skinner (2007), p.58n11. Cites Cohn, Richard (1997). "Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations", Journal of Music Theory41/1.
- ^ David J. Benson, Music: A Mathematical Offering, Cambridge University Press, (2006), p. 385. ISBN 9780521853873.
- ^ Easley Blackwood, Jeffrey Kust, Easley Blackwood: Microtonal, Cedille (1996) ASIN: B0000018Z8.
- ^ Skinner (2007), p.75.
外部連結[编辑]
- Ivor Darreg, "15-TONE SCALE SYSTEM" (1991), Sonic-Arts.org.
- Brewt: 「十五平均律教學」.
| |||||||
