轉動慣量列表

  关于这个物理量的严格定义及其推导过程，请参见转动惯量。

對於一個有多個質點的系統，$I=\sum _{i=1}^{N}{m_{i}r_{i}^{2}}$。若該系統由剛體組成，可以用無限個質點的轉動慣量和，即用積分計算其轉動慣量。以下列表给出了常见物理模型的转动惯量。

值得注意的是，不應將其與截面慣量（又稱截面二次轴矩（second axial moment of area）），截面矩（area moment of inertia）混淆，後者用於彎折方面的計算。以下之轉動慣量假設了整個物體具有均勻的常數密度。

常见物理模型的转动惯量

描述	圖形	轉動慣量	註解
质点，离轴距离为r，质量为m		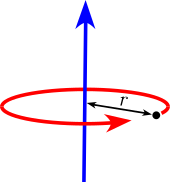$I=mr^{2}\,\!$	—
兩端開通的薄圓柱殼，半徑為r，質量為m		$I=mr^{2}\,\!$	此表示法假設了殼的厚度可以忽略不計。此為下一個物體，當其r1 = r2時的特例。
兩端開通的厚圓柱，內半徑為r1，外半徑為r2，高為h，質量為m		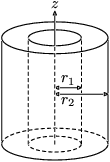$I_{z}={\frac {1}{2}}m\left({r_{1}}^{2}+{r_{2}}^{2}\right)$ $I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{1}}^{2}+{r_{2}}^{2}\right)+h^{2}\right]$ 或者定義標準化厚度tn = t/r並定義r = r2， 可得$I_{z}=mr^{2}\left(1-t_{n}+{\frac {1}{2}}t_{n}^{2}\right)$	—
實心圓柱，半徑為r，高為h，質量為m		$I_{z}={\frac {mr^{2}}{2}}\,\!$ $I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)\,\!$	此為前面物體，當其r1 = 0時的特例。
薄圆盘，半徑為r，質量為m		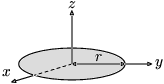$I_{z}={\frac {mr^{2}}{2}}\,\!$ $I_{x}=I_{y}={\frac {mr^{2}}{4}}\,\!$	此為前面物體，當其h = 0時的特例。
圓環，半徑為r，質量為m		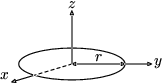$I_{z}=mr^{2}\,\!$ $I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!$	此為後面環面，當其b = 0時的特例。
球壳，内半径为r1，外半径为r2，质量为m		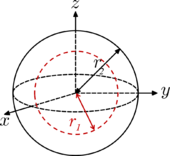$I={\frac {2}{5}}m\left({\frac {{r_{2}}^{5}-{r_{1}}^{5}}{{r_{2}}^{3}-{r_{1}}^{3}}}\right)\,\!$	—
實心球，半徑為r，質量為m		$I={\frac {2mr^{2}}{5}}\,\!$	此为前面物体，当其r1 = 0时的特例；也是后面椭球，当其a = b = c时的特例。
空心球，半徑為r，質量為m		$I={\frac {2mr^{2}}{3}}\,\!$	此为前面球壳，当其r1 → r2时的极限。
椭球，半轴为a、b、c，质量为m		$I_{a}={\frac {1}{5}}m\left(b^{2}+c^{2}\right)\,\!$ $I_{b}={\frac {1}{5}}m\left(a^{2}+c^{2}\right)\,\!$ $I_{c}={\frac {1}{5}}m\left(a^{2}+b^{2}\right)\,\!$	—
圆锥，半徑為r，高為h，質量為m		$I_{z}={\frac {3}{10}}mr^{2}\,\!$ $I_{x}=I_{y}={\frac {3}{20}}m\left({r^{2}}+{4}h^{2}\right)\,\!$	—
實心长方体，高為h，宽為w，长為d，質量為m		$I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)$ $I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)\,\!$ $I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)\,\!$	边长为$s$的立方体对任意过质心的轴的转动惯量$I_{\mathrm {CM} }={\frac {ms^{2}}{6}}\,\!$。
正四面体，边长为s，质量为m		$I_{\mathrm {solid} }={\frac {1}{20}}ms^{2}\,\!$ $I_{\mathrm {hollow} }={\frac {1}{12}}ms^{2}\,\!$	“solid”意为实心，“hollow”意为空心，下同。
正八面体，边长为s，质量为m		$I_{x,\mathrm {hollow} }=I_{y,\mathrm {hollow} }=I_{z,\mathrm {hollow} }={\frac {1}{6}}ms^{2}\,\!$ $I_{x,\mathrm {solid} }=I_{y,\mathrm {solid} }=I_{z,\mathrm {solid} }={\frac {1}{10}}ms^{2}\,\!$	—
细棒，长為L，質量為m		$I_{\mathrm {center} }={\frac {mL^{2}}{12}}\,\!$	此表示法假設了棒的宽度和厚度可以忽略不計。此為前面实心长方体，當其w = L，h = d = 0時的特例。
细棒，长為L，質量為m		$I_{\mathrm {end} }={\frac {mL^{2}}{3}}\,\!$	此表示法假設了棒的宽度和厚度可以忽略不計。
环面，圆管的半徑為a，截面的半徑為b，質量為m		关于直徑：${\frac {1}{8}}\left(4a^{2}+5b^{2}\right)m\,\!$ 关于纵轴：$\left(a^{2}+{\frac {3}{4}}b^{2}\right)m\,\!$	—
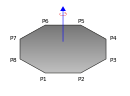薄多边形，顶点為${\vec {P}}_{1}$，${\vec {P}}_{2}$，${\vec {P}}_{3}$，……，${\vec {P}}_{N}$，質量為$m$		$I={\frac {m}{6}}{\frac {\sum _{n=1}^{N}||{\vec {P}}_{n+1}\times {\vec {P}}_{n}||({\vec {P}}_{n+1}^{2}+{\vec {P}}_{n+1}\cdot {\vec {P}}_{n}+{\vec {P}}_{n}^{2})}{\sum _{n=1}^{N}||{\vec {P}}_{n+1}\times {\vec {P}}_{n}||}}$	外接圆半径为R，质量为m的正n边形，对过其中心且垂直于所在平面的轴的转动惯量$I={\frac {1}{2}}mR^{2}\left(1-{\frac {2}{3}}\sin ^{2}{\frac {\pi }{n}}\right)\,\!$

常見物理模型的三維慣量張量

以下列表給出了每個物體主軸上的慣量張量。

為了保留上面的I的標量矩，I的張量矩根據以下式子被投射在由單位向量n所定義的方向上：

$\mathbf {n} \cdot \mathbf {I} \cdot \mathbf {n} \equiv n_{i}I_{ij}n_{j}\,,$

其中點積表示用到了張量收縮和愛因斯坦求和約定。n可以是I_x, I_y, I_z的笛卡爾基e_x, e_y, e_z

描述	圖形	慣量張量矩
實心球，半徑為r，質量為m		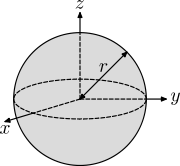$I={\begin{bmatrix}{\frac {2}{5}}mr^{2}&0&0\\0&{\frac {2}{5}}mr^{2}&0\\0&0&{\frac {2}{5}}mr^{2}\end{bmatrix}}$
空心球，半徑為r，質量為m		$I={\begin{bmatrix}{\frac {2}{3}}mr^{2}&0&0\\0&{\frac {2}{3}}mr^{2}&0\\0&0&{\frac {2}{3}}mr^{2}\end{bmatrix}}$
實心椭球，半轴为a、b、c，质量为m		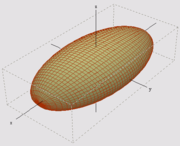$I={\begin{bmatrix}{\frac {1}{5}}m(b^{2}+c^{2})&0&0\\0&{\frac {1}{5}}m(a^{2}+c^{2})&0\\0&0&{\frac {1}{5}}m(a^{2}+b^{2})\end{bmatrix}}$
圆锥，半徑為r，高為h，質量為m		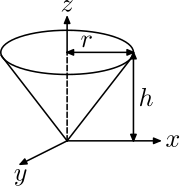$I={\begin{bmatrix}{\frac {3}{5}}mh^{2}+{\frac {3}{20}}mr^{2}&0&0\\0&{\frac {3}{5}}mh^{2}+{\frac {3}{20}}mr^{2}&0\\0&0&{\frac {3}{10}}mr^{2}\end{bmatrix}}$
實心长方体，高為h，宽為w，长為d，質量為m	180x	$I={\begin{bmatrix}{\frac {1}{12}}m(h^{2}+d^{2})&0&0\\0&{\frac {1}{12}}m(w^{2}+d^{2})&0\\0&0&{\frac {1}{12}}m(w^{2}+h^{2})\end{bmatrix}}$
端點繞y軸旋轉的细棒，长為l，質量為m		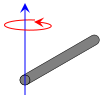$I={\begin{bmatrix}{\frac {1}{3}}ml^{2}&0&0\\0&0&0\\0&0&{\frac {1}{3}}ml^{2}\end{bmatrix}}$
中心繞y軸旋轉的细棒，长為l，質量為m		$I={\begin{bmatrix}{\frac {1}{12}}ml^{2}&0&0\\0&0&0\\0&0&{\frac {1}{12}}ml^{2}\end{bmatrix}}$
實心圓柱，半徑為r，高為h，質量為m		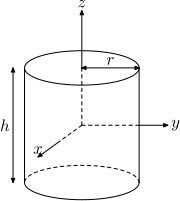$I={\begin{bmatrix}{\frac {1}{12}}m(3r^{2}+h^{2})&0&0\\0&{\frac {1}{12}}m(3r^{2}+h^{2})&0\\0&0&{\frac {1}{2}}mr^{2}\end{bmatrix}}$
兩端開通的厚圓柱，內半徑為r1，外半徑為r2，高為h，質量為m		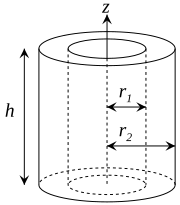$I={\begin{bmatrix}{\frac {1}{12}}m(3(r_{1}^{2}+r_{2}^{2})+h^{2})&0&0\\0&{\frac {1}{12}}m(3(r_{1}^{2}+r_{2}^{2})+h^{2})&0\\0&0&{\frac {1}{2}}m(r_{1}^{2}+r_{2}^{2})\end{bmatrix}}$

相關條目

• 轉動慣量
• 截面慣量列表