Coshc函数 常见于有关光学散射 [ 1] 海森堡时空 [ 2] 双曲几何学 的论文 中[ 3] [ 4] [ 5]
Coshc
(
z
)
=
cosh
(
z
)
z
{\displaystyle \operatorname {Coshc} (z)={\frac {\cosh(z)}{z}}}
它是下列微分方程的一个解:
w
(
z
)
z
−
2
d
d
z
w
(
z
)
−
z
d
2
d
z
2
w
(
z
)
=
0
{\displaystyle w\left(z\right)z-2\,{\frac {d}{dz}}w\left(z\right)-z{\frac {d^{2}}{d{z}^{2}}}w\left(z\right)=0}
Coshc 2D plot Coshc'(z) 2D plot 复域虚部
Im
(
cosh
(
x
+
i
y
)
x
+
i
y
)
{\displaystyle \operatorname {Im} \left({\frac {\cosh(x+iy)}{x+iy}}\right)}
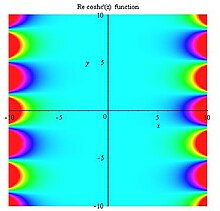
复域实部
Re
(
cosh
(
x
+
i
y
)
x
+
i
y
)
{\displaystyle \operatorname {Re} \left({\frac {\cosh \left(x+iy\right)}{x+iy}}\right)}
绝对值
|
cosh
(
x
+
i
y
)
x
+
i
y
|
{\displaystyle \left|{\frac {\cosh(x+iy)}{x+iy}}\right|}
一阶导数
sinh
(
z
)
z
−
cosh
(
z
)
z
2
{\displaystyle {\frac {\sinh(z)}{z}}-{\frac {\cosh(z)}{z^{2}}}}
导数实部
−
Re
(
−
1
−
(
cosh
(
x
+
i
y
)
)
2
x
+
i
y
+
cosh
(
x
+
i
y
)
(
x
+
i
y
)
2
)
{\displaystyle -\operatorname {Re} \left(-{\frac {1-(\cosh(x+iy))^{2}}{x+iy}}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}}\right)}
导数虚部
−
Im
(
−
1
−
(
cosh
(
x
+
i
y
)
)
2
x
+
i
y
+
cosh
(
x
+
i
y
)
(
x
+
i
y
)
2
)
{\displaystyle -\operatorname {Im} \left(-{\frac {1-(\cosh(x+iy))^{2}}{x+iy}}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}}\right)}
导数绝对值
|
−
1
−
(
cosh
(
x
+
i
y
)
)
2
x
+
i
y
+
cosh
(
x
+
i
y
)
(
x
+
i
y
)
2
|
{\displaystyle \left|-{\frac {1-(\cosh(x+iy))^{2}}{x+iy}}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}}\right|}
Coshc
(
z
)
=
(
i
z
+
1
/
2
π
)
M
(
1
,
2
,
i
π
−
2
z
)
e
1
/
2
i
π
−
z
z
{\displaystyle \operatorname {Coshc} (z)={\frac {\left(iz+1/2\,\pi \right){{\rm {M}}\left(1,\,2,\,i\pi -2\,z\right)}}{{{\rm {e}}^{1/2\,i\pi -z}}z}}}
Coshc
(
z
)
=
1
2
(
2
i
z
+
π
)
H
e
u
n
B
(
2
,
0
,
0
,
0
,
2
1
/
2
i
π
−
z
)
e
1
/
2
i
π
−
z
z
{\displaystyle \operatorname {Coshc} (z)={\frac {1}{2}}\,{\frac {\left(2\,iz+\pi \right){\it {HeunB}}\left(2,0,0,0,{\sqrt {2}}{\sqrt {1/2\,i\pi -z}}\right)}{{{\rm {e}}^{1/2\,i\pi -z}}z}}}
Coshc
(
z
)
=
−
i
(
2
i
z
+
π
)
W
h
i
t
t
a
k
e
r
M
(
0
,
1
/
2
,
i
π
−
2
z
)
(
4
i
z
+
2
π
)
z
{\displaystyle \operatorname {Coshc} (z)={\frac {-i\left(2\,iz+\pi \right){{\rm {\mathbf {W} hittakerM}}\left(0,\,1/2,\,i\pi -2\,z\right)}}{\left(4\,iz+2\,\pi \right)z}}}
Coshc
z
≈
(
z
−
1
+
1
2
z
+
1
24
z
3
+
1
720
z
5
+
1
40320
z
7
+
1
3628800
z
9
+
1
479001600
z
11
+
1
87178291200
z
13
+
O
(
z
15
)
)
{\displaystyle \operatorname {Coshc} z\approx ({z}^{-1}+{\frac {1}{2}}z+{\frac {1}{24}}{z}^{3}+{\frac {1}{720}}{z}^{5}+{\frac {1}{40320}}{z}^{7}+{\frac {1}{3628800}}{z}^{9}+{\frac {1}{479001600}}{z}^{11}+{\frac {1}{87178291200}}{z}^{13}+O\left({z}^{15}\right))}
Coshc abs complex 3D Coshc Im complex 3D plot Coshc Re complex 3D plot
Coshc'(z) Im complex 3D plot Coshc'(z) Re complex 3D plot Coshc'(z) abs complex 3D plot
Coshc'(x) abs density plot Coshc'(x) Im density plot Coshc'(x) Re density plot
^ PN Den Outer, TM Nieuwenhuizen, A Lagendijk,Location of objects in multiple-scattering media,JOSA A, Vol. 10, Issue 6, pp. 1209-1218 (1993)
^ T Körpinar ,New characterizations for minimizing energy of biharmonic particles in Heisenberg spacetime - International Journal of Theoretical Physics, 2014 - Springer
^ Nilg¨un S¨onmez,A Trigonometric Proof of the Euler Theorem in Hyperbolic Geometry,International Mathematical Forum, 4, 2009, no. 38, 1877 - 1881
^ JHM ten Thije Boonkkamp, J van Dijk, L Liu,Extension of the complete flux scheme to systems of conservation laws,J Sci Comput (2012) 53:552–568,DOI 10.1007/s10915-012-9588-5
^ Weisstein, Eric W. "Coshc Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CoshcFunction.html [永久失效連結