朗道-利夫希兹方程
在物理學上,朗道-利夫希兹-吉爾伯特方程(Landau–Lifshitz–Gilbert),是以列夫·達維多維奇·朗道、叶夫根尼·利夫希茨和T·L·吉爾伯特命名的物理方程,以差分方程為基礎闡述一個進動磁性粒子的自發磁化。由T·L·吉爾伯特修改列夫·達維多維奇·朗道、叶夫根尼·利夫希茨的方程得到。该方程可以描述无外场作用下粒子受平均场作用而产生的运动。该方程直接暗示了自旋系统存在孤子。 朗道-利夫希兹方程是非线性偏微分方程,该方程有单一孤子的严格解,对于多孤子情形,可以采取数值方法求解。該方程在在不同情形下模擬微磁性磁場的鐵磁性磁場,尤其孤子於磁場的時閾行為。.[1] 附加方程用於闡述自旋极化电流对磁体的影响。[2]
朗道-利夫希茲方程
[编辑]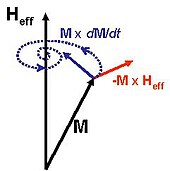
設一個鐵磁體,磁化強度M可在其內部發生變化,但每一點擁有相等的磁飽和強度MS.朗道-利夫希兹-吉爾伯特方程對磁化響應于轉矩的旋轉,引入:[3][4][5]
其中,γ 是孤子旋磁比,λ是現象阻尼參數,則:
其中,α是一个无量纲常数,称为阻尼因子。有效場場Heff為外部場的一個組合時,退磁場(磁化磁場)的量子力學效應。解方程前提是包含用於退磁場的附加方程。
採用不可逆的統計力學法,可獨立推導出朗道-利夫希茲方程。[6]
朗道-利夫希茲-吉爾伯特方程
[编辑]1955年吉爾伯特由一個依賴於磁場的時間導數取代了朗道-利夫希茲的阻尼項:
其中,η 是材料特性的阻尼參數。它可以轉化為朗道-利夫希茲方程:
由此:
此情形的朗道-利夫希茲方程中,進動期γ'依賴於阻尼項。這更好地代表現實中磁體影響時,阻尼較大。
方程形式
[编辑]普通形式
[编辑]该方程的基本思想就是,在规范场作用下,粒子的运动本身会产生电磁场,而这种电磁场可以自我驱动于每一个粒子
协变形式
[编辑]协变情况下,, 这里的速度代表的是粒子运动的群速度。
物理意义
[编辑]平均场引发的自我驱动往往具有自持效果,这种效果的体现就是一群粒子可以形成稳定的孤子波。这就是磁性孤子。
参考文献
[编辑]- Landau-Lifshitz equation, B Guo and S Ding, World Scientific, ISBN 109812778756
- ^ Yang, Bo. Numerical Studies of Dynamical Micromagnetics. [8 August 2011]. (原始内容存档于2017-01-19).
- ^ 存档副本. [2015-07-04]. (原始内容存档于2015-04-07).
- ^ Aharoni 1996
- ^ Brown 1978
- ^ Chikazumi 1997
- ^ T. Iwata, J. Magn. Magn. Mater. 31–34, 1013 (1983); T. Iwata, J. Magn. Magn. Mater. 59, 215 (1986); V.G. Baryakhtar, Zh. Eksp. Teor. Fiz. 87, 1501 (1984); S. Barta (unpublished, 1999); W. M. Saslow, J. Appl. Phys. 105, 07D315 (2009).
延伸閱讀
[编辑]- Amikam Aharoni. Introduction to the Theory of Ferromagnetism. Clarendon Press. 1996. ISBN 0-19-851791-2. (原始内容存档于2011-06-29).
- William Fuller Brown, Jr. Micromagnetics. Robert E. Krieger Publishing Co. 1978 [Originally published in 1963]. ISBN 0-88275-665-6.
- Chikazumi, Sōshin. Physics of Ferromagnetism. Clarendon Press. 1997. ISBN 0-19-851776-9.
- Gilbert, T.L., A Lagrangian formulation of the gyromagnetic equation of the magnetic field, Physical Review, 1955, 100: 1243, Bibcode:1955PhRv..100.1235., doi:10.1103/PhysRev.100.1235. This is only an abstract; the full report is "Armor Research Foundation Project No. A059, Supplementary Report, May 1, 1956", but was never published. A description of the work is given in Gilbert, T. L., A phenomenological theory of damping in ferromagnetic materials, IEEE Trans. Mag., 2004, 40 (6): 3443–3449, Bibcode:2004ITM....40.3443G, doi:10.1109/TMAG.2004.836740
- Landau, L.D.; Lifshitz, E.M., Theory of the dispersion of magnetic permeability in ferromagnetic bodies, Phys. Z. Sowietunion, 1935, 8, 153
- Skrotskiĭ, G V, The Landau-Lifshitz equation revisited, Sov. Phys. Usp., 1984, 27 (12): 977–979, Bibcode:1984SvPhU..27..977S, doi:10.1070/PU1984v027n12ABEH004101
- Guo, Boling; Ding, Shijin, Landau-Lifshitz Equations, Frontiers of Research With the Chinese Academy of Sciences, World Scientific Publishing Company, 2008, ISBN 978-981-277-875-8
- Cimrak, Ivan, A Survey on the Numerics and Computations for the Landau-Lifshitz Equation of Micromagnetism (PDF), Archives of Comp. Meth. Eng., 2007, 15 (3): 1–37 [2015-07-04], doi:10.1007/BF03024947, (原始内容 (PDF)存档于2015-07-05)
- M, Lakshmanan, The fascinating world of the Landau–Lifshitz–Gilbert equation: an overview (PDF), Phil. Trans. R. Soc. A, 2010, 369 (1939): 1280–1300, Bibcode:2011RSPTA.369.1280L, arXiv:1101.1005
 , doi:10.1098/rsta.2010.0319
, doi:10.1098/rsta.2010.0319








