自由膨胀

自由膨胀，在隔热腔室中，从体积V_i = V₀膨胀到体积V_f = 2V₀

气体的自由膨胀可以快速将活塞外推，推动速度比气体中移动最快分子还快的速度实现

自由膨胀不可逆，但对每个腔室可以是准静态的：每个部份都是准热力学平衡，但对整个系统而言则不然

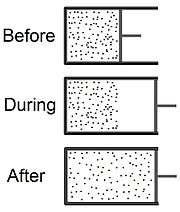
自由膨胀（英语：free expansion）也称为焦耳膨胀，是一种不可逆的热力学过程，过程中气体在一个绝热的系统内，一开始气体只在系统的部份区域，和其他部份用隔板隔开，之后突然移除隔板，使气体膨胀，外界和系统之间没有功和热的交换。

自由膨胀是一个有关理想气体的思想实验，可以探讨古典热力学的现象。这个例子可以用来计算热力学物理量的变化，包括因为此过程的不可逆，造成整体熵的增加（熵产生量）。针对理想气体的自由膨胀，过程前后的温度不会变化，而且过程前后的状态符合以下的式子

p_i V_i = p_f V_f,

其中p为压力，V为体积而下标的i及f表示初始及结束的状态。

实际的自由膨胀会和实际气体的特性有关，这类过程中的温度变化可以量测分子间作用力。

焦耳膨胀的名称是得名自詹姆斯·焦耳，他在1845年研究功和热时有使用膨胀，但此过程在焦耳之前就已为人所知，例如约翰·莱斯利在19世纪初就已知道，约瑟夫·路易·盖-吕萨克在1807年也研究，得到和焦耳类似的结果。

说明

此过程开始于某压力$P_{\mathrm {i} }$、某温度$T_{\mathrm {i} }$的气体，限制在某隔热容器中的一半空间（可参考此条目最上方的图）。气体的初始体积为$V_{\mathrm {i} }$，和容器的另一半空间（体积$V_{\mathrm {0} }$）已用机构隔开, 而另一半空间的压力是零。若两半空间之间的分隔突然移除，气体会膨胀充满整个容器，其总体积是$V_{\mathrm {f} }=V_{\mathrm {i} }+V_{\mathrm {0} }$。在容器的左半边有插入温度计，量测膨胀前后的气体热力学温度。

这个实验的热力学系统包括容器的两个半边，也就是实验结束时气体所充满的空间。因为系统隔热，无法和周围交换热量。因为总体积不变，外界也无法对系统作功。因此，内能变化$\Delta U$为零。内能包括内部的动能（因为分子移动）以及内部位能（因为分子间作用力）。当分子随机运动时，温度是对内部动态的量测。此例中，内部动态即为热。若腔室没有达到平衡，会有动能的流动，这部份是温度计无法侦测的（因此不是热的成份之一）。因此，温度的变化表示动能的变化，一直要到重新达到热平衡，才能完全看到此变化。当热以动能流动的方式传输，会让温度下降。 实务上，简单的两腔室自由膨胀常会加入多孔塞，膨胀的气体需通过多孔塞才能到低压的腔室。此目的是为了禁止方向性的流动，加快热平衡的重新建立。 因为总内能没有变化，腔室中的停滞流让动能又转换为气体的随机运动（热），因此温度会上升到预期温度。 若初始空气压力够低，让非理想气体成份凝结，一些内能会转换为液体的潜热（位能的变化）。因此，低温下的自由膨胀提供了分子间作用力的资讯。

理想气体

若是理想气体，其初始状态（$T_{\mathrm {i} }$, $P_{\mathrm {i} }$, $V_{\mathrm {i} }$）和最终状态（$T_{\mathrm {f} }$, $P_{\mathrm {f} }$, $V_{\mathrm {f} }$）会依照理想气体定律，一开始时 $$P_{\mathrm {i} }V_{\mathrm {i} }=nRT_{\mathrm {i} }$$ 隔板打开后 $$P_{\mathrm {f} }V_{\mathrm {f} }=nRT_{\mathrm {f} }.$$

此处$n$是气体莫耳数，$R$是莫耳理想气体常数。因为内能没有变化，而理想气体的内能只是温度的函数，因此温度没有变化，$T_{\mathrm {i} }=T_{\mathrm {f} }$。这表示 $$P_{\mathrm {i} }V_{\mathrm {i} }=P_{\mathrm {f} }V_{\mathrm {f} }=nRT_{\mathrm {i} }.$$

若体积加倍，压力会减半。

温度不会变化的事实，方便计算整体熵的变化。

真实气体

真实气体的自由膨胀和理想气体不同，真实气体自由膨胀后，温度会变化。若温度比反转温度（inversion temperature）要低，气体在自由膨胀后会降温，若温度比反转温度高，在自由膨胀后，气体温度会上升。一般来言，气体的反转温度会高于室温，只有氦气（反转温度约40 K）和氢气（反转温度约200 K）例外。因为自由膨胀过程中，内能是定值，自由膨胀过程中的降温是因为内部动能转换为位能，昇温则是内部位能转换为动能。

相关条目

• 焦耳-汤姆孙效应：气体从高压区透过阀或是多孔塞进入低压区的过程。

参考资料

大部份大学教科书都对此主题说明的很深入，例如Concepts in Thermal Physics, Blundell & Blundell, OUP ISBN 0-19-856770-7