藤村幸三郎的三角形問題

藤村幸三郎的三角形問題(Kobon triangle problem)是一個離散幾何上未解決的問題,該問題首先由藤村幸三郎(Kobon Fujimura)提出。這個問題問說「對k條線進行排列,則在此直線排列(Arrangement of lines)中,以這k條線為邊且彼此不重疊的三角形最多有多少個?」。一些此問題的變體問的是在射影平面上的狀況,且要求其中的三角形不能為該直線排列中的各線給穿過。[1]
田村三郎證明說此問題的最大整數解之值不超過,這為「對k條線進行排列,則在此直線排列(Arrangement of lines)中,以這k條線為邊且彼此不重疊的三角形的數量的最大值」解提供了一個上界。[2]
在2007年,約翰尼斯‧巴德(Johannes Bader)和吉萊‧克雷蒙(Gilles Clément)發現了一個較小的上界,他們證明說當k除以6的餘數為0或2時,該k值對此問題答案的上界會比田村氏所給出的上界要來得小。[3]在這些k值中,其上界值會為田村氏給出的上界值減一。
此問題的「完美解」(與理論最大值相合的已知最佳解)在k = 3, 4, 5, 6, 7, 8, 9, 13, 15 和 17的狀況下是已求出的[4] ;在k = 10, 11 和 12的狀況下,目前已知的最佳解比其理論上界要小一個值。
藉由使用佛吉(D. Forge)和羅米瑞茲─阿爾豐森(J. L. Ramirez Alfonsin)兩氏提供的方法[1][5],在已知k0條線狀況下的完美解的狀況下,亦可知此問題對形如的各數字ki的(完美)解,像例如當k0 = 3時,在k = 3,5,9,17,33,65,...等的狀況下,「對k條線進行排列,則在此直線排列(Arrangement of lines)中,以這k條線為邊且彼此不重疊的三角形的數量的最大值」亦可求出。
| k | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | OEIS |
| 田村氏的上界 | 1 | 2 | 5 | 8 | 11 | 16 | 21 | 26 | 33 | 40 | 47 | 56 | 65 | 74 | 85 | 96 | 107 | 120 | 133 | A032765 |
| 克雷蒙與巴德二氏的上界 | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 26 | 33 | 39 | 47 | 55 | 65 | 74 | 85 | 95 | 107 | 119 | 133 | - |
| 已知的最佳解 | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 25 | 32 | 38 | 47 | 53 | 65 | 72 | 85 | 93 | 104 | 115 | 130 | A006066 |
範例
[編輯]-
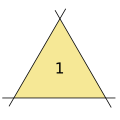
三條直線的狀況,此情況下為一三角形
-
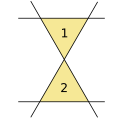
四條直線的狀況
-
五條直線的狀況
-
六條直線的狀況
-
七條直線的狀況
參照
[編輯]- ^ 1.0 1.1 Forge, D.; Ramírez Alfonsín, J. L., Straight line arrangements in the real projective plane, Discrete and Computational Geometry, 1998, 20 (2): 155–161, doi:10.1007/PL00009373.
- ^ Weisstein, Eric W. (編). Kobon Triangle. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ G. Clément and J. Bader. Tighter Upper Bound for the Number of Kobon Triangles. Draft Version, 2007. (PDF). [2013-05-23]. (原始內容 (PDF)存檔於2017-11-11).
- ^ Ed Pegg Jr. on Math Games. [2013-05-23]. (原始內容存檔於2013-06-02).
- ^ "Matlab code illustrating the procedure of D. Forge and J. L. Ramirez Alfonsin", Retrieved on 9 May 2012.. [2013-05-23]. (原始內容存檔於2021-03-08).
外部連結
[編輯]- Johannes Bader, "Kobon Triangles"