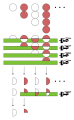
English: Euler summation of
1 − 2 + 3 − 4 + · · · to 1/2-1/4.
The original series 1 − 2 + 3 − 4 + · · · is depicted at the top of the diagram; the Euler transformed series 1/2 − 1/4 + 0 + 0 + · · · is depicted at the bottom of the diagram. The conclusion is that the Euler sum of 1 − 2 + 3 − 4 + · · · is 1/2-1/4 = 1/4.
Only the first four terms of the series are shown. A white disk represents +1; a reddish disk represents −1. The units are grouped on top of each other as they occur within the terms of the series.
Let a = 1 − 2 + 3 − 4 + · · · be the original formal series. Let S be the shift operator on formal series,

Let T be the average between S and the identity operator:

Then given a series a, if it converges, then its sum is the same as the sum of the series

The Euler summation procedure has many descriptions, but for the present purposes it can be described as a repetition of the above "process". To be precise, the nth term of the Euler transformed series is

See eq. (20.3) of Korevaar, Jacob (2004年) 《 Tauberian Theory: A Century of Developments》、Springer、pp. 326 ISBN 3-540-21058-X
To compute this transform in place, one pulls half of each term into the next term, then fixes the first term, then repeats.
The part of the diagram with the four green stripes indicates taking half of every term in the original series a and pulling it into the next term. Most of the units cancel, leaving the series

The first term of this series is fixed, leaving

The process repeated upon the remaining terms, leaving 1/2 − 1/4 + 0 + 0 + · · ·. Now two terms are fixed, and the remaining terms are all zero, so all further applications of T do not change the series, and they are not depicted. In the visual language, subsequent green stripes pull on nothingness.
The result is the Euler transformed series, 1/2 − 1/4 + 0 + 0 + · · ·. It is convergent, having only two nonzero terms, and its sum is 1/2 − 1/4. The diagram does not distinguish between the finite series and its sum. As a number, 1/2 − 1/4 = 1/4.
The above is done to illustrate
how Euler summation works on the series. In practice, one exploits auxiliary quantities, and the computation is much easier; see for example
Image:Pm1234-Euler1755.png. An extended description of Euler's procedure on 1 − 2 + 3 − 4 + · · ·, including reversing its alternation and taking iterated forward differences, is at
w:1 − 2 + 3 − 4 + · · ·#Euler and Borel.