描述函数
描述函数(describing function)是控制系统中用近似方式处理非线性系统的方法,由Nikolay Mitrofanovich Krylov及尼古拉·博戈柳博夫在1930年代提出[1][2],后来由Ralph Kochenburger延伸[3]。描述函数是以准线性为基础,是用会依输入波形振幅而变化的线性时不变传递函数来近似非线性系统的作法。依照定义,真正线性时不变系统的传递函数不会随输入函数的振幅而变化(因为是线性系统)。因此,其和振幅的相依性就会产生一群的线性系统,这些系统结合起来的目的是为了近似非线性系统的特性。描述函数是少数广为应用来设计非线性系统的方法,描述函数是在分析闭回路控制器(例如工业过程控制、伺服机构、电子振荡器)的极限环时,常见的数学工具。
原理[编辑]
考虑一个慢速,稳定的线性系统,其回授路径中有不连续(但有分段连续)的非线性特性(例如有饱和的放大器、或是有死区效应的元件)。在非线性元件上看到的连续区域会视线性系统的振幅而定。若线性系统输出的振幅变小,其非线性元件的特性可能又会变换到另一个区域。这种在二个连续区间之间的切换会造成周期性的振荡。描述函数方式法目的是要预设这些振荡的特性(也就是其基频),作法是假设慢速系统特性类似低通滤波器或带通滤波器,会将能量集中在单一频率。即使输出波形有多个不同的模态,描述函数仍可以提供有关频率的资讯,也许也包括振幅相关的资讯。此情形下,描述函数有点类似在描述回授系统的滑动模式。
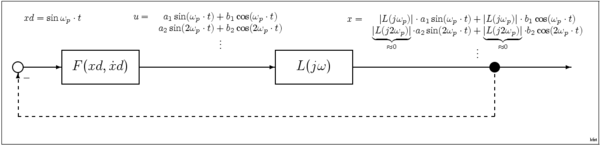
利用低通滤波器的假设,系统响应可以表示为一组正弦曲线中的一个弦波。此情形下,系统可以表示为弦波描述函数(SIDF),是对振幅为A,频率为的弦波输入的系统响应。SIDF是描述线性函数传递函数 的变体。在准线性系统中,输入信号为弦波时,其输出也是相同频率的弦波,但其振幅及相位的关系可以用表示。以此观点来看,许多系统在弦波输入下的响应虽不一定是纯弦波,但大部分输出能量集中在是和输入信号相同的频率,因此可以近似为准线性系统。其原因是这类系统在其本质上有低通或是带通的特性,因此高次的谐波受到了抑制,也有可能是特意加入了滤波器。弦波描述函数(SIDF)的重要用途之一是消除弦波电子振荡器的非理想讯号。
考虑非线性系统,在弦波输入下,其描述函数可以表示为,其中的实部g及虚部b可以表示如下:
也有其他型式的描述函数,例如水平输入以及高斯噪声输入的描述函数。描述函数无法完整的描述系统,不过多半已可以处理像是控制或是稳定性的问题。描述函数最适用于分析非线性程度相对轻微的系统。此外,高阶弦波输入描述函数(HOSIDF)描述非线性系统在弦波输入下,其各阶谐波成分的振幅及相位。高阶弦波输入描述函数是描述函数是延伸版本,用在响应的非线性程度非常明显的场合。
注意事项[编辑]
在许多种类的系统中,描述函数都可以产生一定准确度的结果,不过也有些情形会失效。例如在一些很强调其高阶谐波特性的系统,描述函数就不一定能发挥作用。Tzypkin曾经用起停式控制系统为例说明过[4]。另一个比较简单的例子是由非反相施密特触发器加上反相积分器组成的闭回路振荡器,以积分器的输出为施密特触发器的输入。施密特触发器的输出是方波,而积分器的输出是三角波,的三角波的波峰恰好就是方波的切换点。振荡器中的这两部分输出都落后输入90度。若是用描述函数来处此一电路,施密特触发器的输入会变成频率为其基频的弦波,通过触发器也会有延迟,但会比90度要小(弦波触发触发器的时机会比三角波要快),因此描述函数下,系统振荡的方式会和原系统的不同[5]。
若是符合阿依热尔曼猜想或卡尔曼猜想的条件,可能利用描述函数找不到周期解[6][7],相反的,也有周期解的反例(隐藏振荡)。因此描述函数的应用也需要确认是否适合[8][9]。
参考资料[编辑]
- ^ Krylov, N. M.; N. Bogoliubov. Introduction to Nonlinear Mechanics. Princeton, US: Princeton Univ. Press. 1943 [2019-05-02]. ISBN 0691079854. (原始内容存档于2013-06-20).
- ^ Blaquiere, Austin. Nonlinear System Analysis. Elsevier Science. : 177. ISBN 0323151663.
- ^ Kochenburger, Ralph J. A Frequency Response Method for Analyzing and Synthesizing Contactor Servomechanisms. Trans. AIEE (American Institute of Electrical Engineers). January 1950, 69 (1): 270–284 [June 18, 2013]. doi:10.1109/t-aiee.1950.5060149. (原始内容存档于2016-03-04).
- ^ Tsypkin, Yakov Z. Relay Control Systems. Cambridge: Univ Press. 1984.
- ^ Boris Lurie; Paul Enright. Classical Feedback Control: With MATLAB. CRC Press. 2000: 298–299. ISBN 978-0-8247-0370-7.
- ^ Leonov G.A.; Kuznetsov N.V. Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems (PDF). Doklady Mathematics. 2011, 84 (1): 475–481 [2019-05-02]. doi:10.1134/S1064562411040120. (原始内容存档 (PDF)于2016-03-04).,
- ^ Aizerman's and Kalman's conjectures and describing function method (PDF). [2019-05-02]. (原始内容存档 (PDF)于2016-03-04).
- ^ Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits (PDF). Journal of Computer and Systems Sciences International. 2011, 50 (4): 511–543 [2019-05-02]. doi:10.1134/S106423071104006X. (原始内容存档 (PDF)于2016-03-04).
- ^ Leonov G.A.; Kuznetsov N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. International Journal of Bifurcation and Chaos. 2013, 23 (1): art. no. 1330002 [2019-05-02]. doi:10.1142/S0218127413300024. (原始内容存档于2019-03-24).
延伸阅读[编辑]
- N. Krylov and N. Bogolyubov: Introduction to Nonlinear Mechanics, Princeton University Press, 1947
- A. Gelb and W. E. Vander Velde: Multiple-Input Describing Functions and Nonlinear System Design (页面存档备份,存于互联网档案馆), McGraw Hill, 1968.
- James K. Roberge, Operational Amplifiers: Theory and Practice, chapter 6: Non-Linear Systems (页面存档备份,存于互联网档案馆), 1975; free copy courtesy of MIT OpenCourseWare 6.010 (2013); see also (1985) video recording of Roberge's lecture on describing functions (页面存档备份,存于互联网档案馆)
- P.W.J.M. Nuij, O.H. Bosgra, M. Steinbuch, Higher Order Sinusoidal Input Describing Functions for the Analysis of Nonlinear Systems with Harmonic Responses, Mechanical Systems and Signal Processing, 20(8), 1883–1904, (2006)








