大间隔最近邻居(Large margin nearest neighbor (LMNN))分类算法是统计学的一种机器学习算法。该算法是在 近邻分类其中学习一种欧式距离度量函数。该度量函数优化的目标是:对于一个输入
近邻分类其中学习一种欧式距离度量函数。该度量函数优化的目标是:对于一个输入 的
的 个近邻都属于同一类别,而不同类别的样本与
个近邻都属于同一类别,而不同类别的样本与 保持一定大的距离。
保持一定大的距离。 近邻规则是模式识别领域广泛使用的一种简单有效的方法。它的效果的好坏只依赖于确定最近邻的距离度量。基于欧式距离度量学习函数的大间隔最近邻居分类算法能够很好的改善
近邻规则是模式识别领域广泛使用的一种简单有效的方法。它的效果的好坏只依赖于确定最近邻的距离度量。基于欧式距离度量学习函数的大间隔最近邻居分类算法能够很好的改善 近邻算法分类效果。[1]
近邻算法分类效果。[1]
大间隔最近邻居算法的主要想法就是通过学习一种距离度量使得在一个新的转换空间中,对于一个输入 的
的 个近邻都属于同一类别,而不同类别的样本与
个近邻都属于同一类别,而不同类别的样本与 保持一定大的距离。如果该想法能够实现则留一(LOO)分类错误率将会最小化。该算法的最主要的任务就是求得满足条件的线性空间转换矩阵
保持一定大的距离。如果该想法能够实现则留一(LOO)分类错误率将会最小化。该算法的最主要的任务就是求得满足条件的线性空间转换矩阵 。
定义有类别标签的训练数据集为:
。
定义有类别标签的训练数据集为: , 其中类别标签集为:
, 其中类别标签集为: .
我们的目标是学习一种用来估计如下平方距离的线性变换
.
我们的目标是学习一种用来估计如下平方距离的线性变换 :
:

其中 是半正定矩阵。欧氏距离是该距离度量的特例(
是半正定矩阵。欧氏距离是该距离度量的特例( 为单位矩阵的形式)。该度量算法也被称作是马氏距离度量(Mahalanobis Metric)。
图1显示了,该算法的学习过程:
为单位矩阵的形式)。该度量算法也被称作是马氏距离度量(Mahalanobis Metric)。
图1显示了,该算法的学习过程:
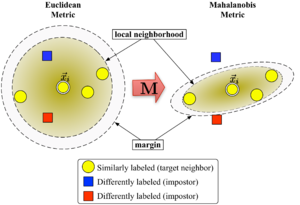 Figure 1: Schematic illustration of LMNN.
Figure 1: Schematic illustration of LMNN.
目标邻居的定义[编辑]
对于每一个输入样本 ,除了要知道其类别标签
,除了要知道其类别标签 外,还需要确定其
外,还需要确定其 个目标邻居,即
个目标邻居,即 个同类别的输入,并且希望通过上式求出的距离最小。当缺乏先验知识的话,属于同类别的目标邻居可以由欧氏距离确定。则属于同类别的
个同类别的输入,并且希望通过上式求出的距离最小。当缺乏先验知识的话,属于同类别的目标邻居可以由欧氏距离确定。则属于同类别的 个的输入即为目标邻居。
个的输入即为目标邻居。
入侵样本的定义[编辑]
对于任何一个输入样本 ,其入侵样本是指与其最近邻的
,其入侵样本是指与其最近邻的 个样本中与其不同类的样本。该算法在对训练样本学习过程中应尽可能的使入侵样本的数目达到最小化。
个样本中与其不同类的样本。该算法在对训练样本学习过程中应尽可能的使入侵样本的数目达到最小化。
大间隔最近邻居算法的转换矩阵 可以通过半定规划得到优化。该算法的目标是:对于每一个输入样本,其
可以通过半定规划得到优化。该算法的目标是:对于每一个输入样本,其 个目标邻居应尽可能的接近,而那些入侵样本应尽可能的远离该输入样本(即与其保持一定大的距离间隔)。图1显示了该算法的学习过程,通过学习使得输入向量
个目标邻居应尽可能的接近,而那些入侵样本应尽可能的远离该输入样本(即与其保持一定大的距离间隔)。图1显示了该算法的学习过程,通过学习使得输入向量 被其目标近邻包围。对于一个测试样本,我们取
被其目标近邻包围。对于一个测试样本,我们取 为3的最近邻规则。
第一个优化的目标是实现输入样本
为3的最近邻规则。
第一个优化的目标是实现输入样本 与其目标近邻的平均距离的最小化:
与其目标近邻的平均距离的最小化:
 .
.
第二个优化的目标是使输入样本 到其目标邻居的距离与其到入侵近邻的距离至少保持1个单位的间隔。该约束可以表示为:
到其目标邻居的距离与其到入侵近邻的距离至少保持1个单位的间隔。该约束可以表示为:

因此,最终的优化问题可以表示为:





其中 为半定矩阵。
为半定矩阵。
参考文献[编辑]
外部链接[编辑]















