大間隔最近鄰居(Large margin nearest neighbor (LMNN))分類算法是統計學的一種機器學習算法。該算法是在 近鄰分類其中學習一種歐式距離度量函數。該度量函數優化的目標是:對於一個輸入
近鄰分類其中學習一種歐式距離度量函數。該度量函數優化的目標是:對於一個輸入 的
的 個近鄰都屬於同一類別,而不同類別的樣本與
個近鄰都屬於同一類別,而不同類別的樣本與 保持一定大的距離。
保持一定大的距離。 近鄰規則是模式識別領域廣泛使用的一種簡單有效的方法。它的效果的好壞只依賴於確定最近鄰的距離度量。基於歐式距離度量學習函數的大間隔最近鄰居分類算法能夠很好的改善
近鄰規則是模式識別領域廣泛使用的一種簡單有效的方法。它的效果的好壞只依賴於確定最近鄰的距離度量。基於歐式距離度量學習函數的大間隔最近鄰居分類算法能夠很好的改善 近鄰算法分類效果。[1]
近鄰算法分類效果。[1]
大間隔最近鄰居算法的主要想法就是通過學習一種距離度量使得在一個新的轉換空間中,對於一個輸入 的
的 個近鄰都屬於同一類別,而不同類別的樣本與
個近鄰都屬於同一類別,而不同類別的樣本與 保持一定大的距離。如果該想法能夠實現則留一(LOO)分類錯誤率將會最小化。該算法的最主要的任務就是求得滿足條件的線性空間轉換矩陣
保持一定大的距離。如果該想法能夠實現則留一(LOO)分類錯誤率將會最小化。該算法的最主要的任務就是求得滿足條件的線性空間轉換矩陣 。
定義有類別標籤的訓練數據集為:
。
定義有類別標籤的訓練數據集為: , 其中類別標籤集為:
, 其中類別標籤集為: .
我們的目標是學習一種用來估計如下平方距離的線性變換
.
我們的目標是學習一種用來估計如下平方距離的線性變換 :
:

其中 是半正定矩陣。歐氏距離是該距離度量的特例(
是半正定矩陣。歐氏距離是該距離度量的特例( 為單位矩陣的形式)。該度量算法也被稱作是馬氏距離度量(Mahalanobis Metric)。
圖1顯示了,該算法的學習過程:
為單位矩陣的形式)。該度量算法也被稱作是馬氏距離度量(Mahalanobis Metric)。
圖1顯示了,該算法的學習過程:
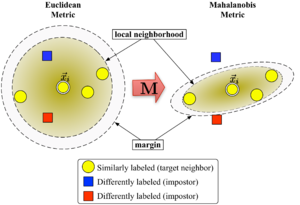 Figure 1: Schematic illustration of LMNN.
Figure 1: Schematic illustration of LMNN.
對於每一個輸入樣本 ,除了要知道其類別標籤
,除了要知道其類別標籤 外,還需要確定其
外,還需要確定其 個目標鄰居,即
個目標鄰居,即 個同類別的輸入,並且希望通過上式求出的距離最小。當缺乏先驗知識的話,屬於同類別的目標鄰居可以由歐氏距離確定。則屬於同類別的
個同類別的輸入,並且希望通過上式求出的距離最小。當缺乏先驗知識的話,屬於同類別的目標鄰居可以由歐氏距離確定。則屬於同類別的 個的輸入即為目標鄰居。
個的輸入即為目標鄰居。
對於任何一個輸入樣本 ,其入侵樣本是指與其最近鄰的
,其入侵樣本是指與其最近鄰的 個樣本中與其不同類的樣本。該算法在對訓練樣本學習過程中應儘可能的使入侵樣本的數目達到最小化。
個樣本中與其不同類的樣本。該算法在對訓練樣本學習過程中應儘可能的使入侵樣本的數目達到最小化。
大間隔最近鄰居算法的轉換矩陣 可以通過半定規劃得到優化。該算法的目標是:對於每一個輸入樣本,其
可以通過半定規劃得到優化。該算法的目標是:對於每一個輸入樣本,其 個目標鄰居應儘可能的接近,而那些入侵樣本應儘可能的遠離該輸入樣本(即與其保持一定大的距離間隔)。圖1顯示了該算法的學習過程,通過學習使得輸入向量
個目標鄰居應儘可能的接近,而那些入侵樣本應儘可能的遠離該輸入樣本(即與其保持一定大的距離間隔)。圖1顯示了該算法的學習過程,通過學習使得輸入向量 被其目標近鄰包圍。對於一個測試樣本,我們取
被其目標近鄰包圍。對於一個測試樣本,我們取 為3的最近鄰規則。
第一個優化的目標是實現輸入樣本
為3的最近鄰規則。
第一個優化的目標是實現輸入樣本 與其目標近鄰的平均距離的最小化:
與其目標近鄰的平均距離的最小化:
 .
.
第二個優化的目標是使輸入樣本 到其目標鄰居的距離與其到入侵近鄰的距離至少保持1個單位的間隔。該約束可以表示為:
到其目標鄰居的距離與其到入侵近鄰的距離至少保持1個單位的間隔。該約束可以表示為:

因此,最終的優化問題可以表示為:





其中 為半定矩陣。
為半定矩陣。















