应力-应变曲线
此條目或其章節极大或完全地依赖于某个单一的来源。 (2015年9月26日) |

1: 彈力限(比例限,虎克定律此後不成立)
2: 偏位降伏強度(0.2%的應變再依弹性模量延伸)
某一种特定材料的应力与应变关系称为该材料的应力-应变曲线(stress-strain curve)。 每一种材料都有唯一的应力-应变曲线,该曲线可以通过记录材料在不同的拉伸和压缩加载(应力)下的形变(应变)来获得。这条曲线也提供了很多该材料的特性,例如其弹性模量、降伏強度(彈力限)、極限拉伸強度,也可以看出材料是脆性材料還是延展性材料[1]。
一般而言,有關任何變形下,应力和应变的關係都可以視為是应力-应变曲线。应力和应变可以是正應力及正應變,剪應力及剪應變,也可以是混合的。可以是單一軸向、雙軸或是多軸的,甚至可以是時變的。變形可以是壓縮、拉伸、扭转、轉動等。若沒有特別標明,应力-应变曲线是指在拉伸測試下正向應力及正向應變之間的關係。
考慮一截面積為A的棒狀物體,其兩端施加大小相等,方向相反的拉伸力。材料會受到應力(定義為受力和其截面積之間比值),也會有軸向的伸長:
其中下標0是材料的原始尺寸,應力的SI單位是牛頓每平方米(N/m2),或是Pa(1 Pa = 1 N/m2),應變為無因次量。
在拉伸試驗下,記錄不同應變下,材料應力的變化,一直到材料斷裂為止,描繪其曲線,即為应力-应变曲线。一般而言,应力-应变曲线會用應變為x軸,應力為y軸。為了工程的需求,一般會假設材料在整個拉伸過程中,其截面積不會變化,不過在變形過程中,截面積也會略為變小。在假設截面積不變的條件下所畫的应力-应变曲线稱為「工程应力-应变曲线」,考慮真正截面積變化的应力-应变曲线稱為「真应力-应变曲线」。
曲線的不同階段
[编辑]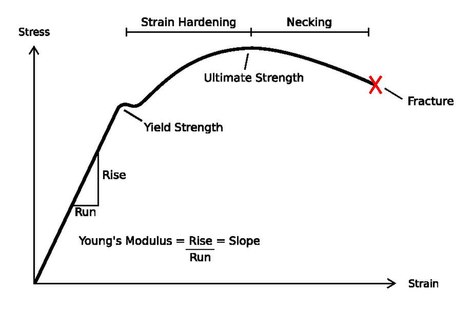
右圖是室溫下低碳鋼的应力-应变曲线,曲線的不同階段有不同的特性,也有不同的機械性質。而其他材料也可能會省略其中的一些階段,或是出現其他的階段。
第一階段是線性彈性階段。此階段的應力和應變成正比,遵守胡克定律,其斜率即為杨氏模量。材料在這個階段的變形都是彈性變形,此階段的結束是塑性變形的開始,該點的應力即為降伏強度(或是上降伏點,簡稱UYP)。
第二階段是應變硬化階段。其應力超過降伏強度,小於極限強度(ultimate strength point)。極限強度是應力-應變曲線的最高點。這個區域一開始的應力不隨應變變化,有短暫的水平區,之後,其應力隨著材料伸長而變大。平坦區的應力稱為下降伏點(LYP),是因為賴得帶的形成及傳遞所造成。明顯的,非均質塑性變形會在上降伏強度形成賴得帶,將變形擴散到下降伏強度的材料。當材料再度均勻變形時,隨著材料的伸展,其應力會增加,這稱為加工硬化。因為塑性變形引起的緻密位錯使位錯無法再進一步發展。為了要克服這種阻礙,需要加較大的臨界分解剪應力。在應變累積時,材料也就在進行加工硬化,一直到應力到達極限強度為止。
第三階段是頸縮階段,應力超過極限強度後,試料中會出現頸縮(Necking)現象,也就是某一段的截面積明顯比平均截面積要小。頸縮變形是非均質的,因為應力在截面積較小的區域更容易集中,因此頸縮會自我增強,讓應力更集中。這種正回授會讓頸縮很快就生成,並且很快斷裂。不過此時拉力雖在減少,但其加工硬化仍在進行中。此時用真實截面積計算的真應力會繼續增加,但假設截面積不變的工程應力就會減少。第三階段的最後是材料的斷裂。在斷裂後可以計算材料的伸長量以及截面積的縮減量。
真實應力和應變之間的關係
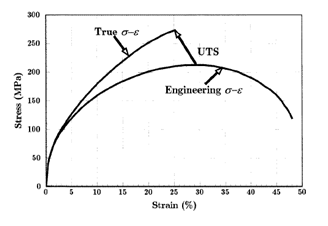
[编辑]真實應力和應變的關係會考慮到截面積縮小對應力的影響,以及因應變參考長度使用當時長度(而不是原始長度)造成的應變降低,和工程應力及應變之間的關係有些不同。
此處的尺寸是即時值,假設物體體積守恆,變形是均勻的出現。
真實應力和應變可以用工程應力及應變表示。針對真實應力
針對應變
兩邊積分,再考慮邊界條件
因此在張力測試中,真實應力會大於工程應力,真實應變小於工程應變。在真實應力-應變圖上有一個點,而其對應的等效工程應力及應變點會往左上方移。真實應力及工程應力的差值會隨著塑性變形增加而變大。在低應變時(例如線性形變),兩者的差值可以省略。對於抗張強度的點,是工程應力-應變曲線的最大點,但不是真應力-應變曲線的最大點。因為工程應力和施力成正比,頸縮形變的判斷基準可以用來計算:
上述分析考慮到抗張強度的本質,抗張強度點時,加工硬化(又称应变硬化)的效果恰好和截面積減少的效果相抵消。
在頸縮形變後,材料承受的是非均質的形變,因此上述公式不再有效。頸縮時的應力及應變可以表示為:
以下的經驗式常用來描述真實應力和應變之間的關係。
上述的n是應變硬化係數,K是強度係數。n可以用來衡量材料加工硬化的特化,n越大的越不容易頸縮。一般而言,金屬在室溫下的n從0.02至0.5之間[2]
分類
[编辑]在許多不同的材料中,可以依應力-應變曲線的特性將材料分為二類:分別是延展性(ductile)材料及脆性(brittle)材料[3]。
延展性材料
[编辑]
具有延展性的材料,包括結構鋼,以及許多其他金屬的合金,可以依其在室溫下降伏的情形來區分其特性[4]。
低碳鋼的应力-应变關係,在降伏強度以下都非常的線性,這段線性區域即為彈性區,斜率為弹性模量或杨氏模量。 許多延展性的材料(包括一些金屬、塑料以及陶瓷)都有降伏點。塑性流動從上降伏點開始,在下降伏點繼續塑性流動。在下降伏點時,永久變形會在試料中不均勻的分佈。在上降伏點形成的變形帶會在下降伏點時延著标距长度傳播。在魯德(luders)應變時,變形帶會佔據整個标距长度。超過這點後,就會出現加工硬化。降伏點的出現對應材料中差排的钉扎点。例如在差排處出現固溶體,就會有钉扎點的效果,使差排無法再移動。因此,需要較大的力才能使差排再移動。若差排離開钉扎点,需要的應力就會比較小。
應變超過降伏點後,因為差排離開科氏氣團,曲線會略為下降。若繼續變形,會因為應變硬化而使應力增加,直到到達極限拉伸強度為止。到達時,會因為泊松收縮的影響使截面積減少。因此試料開始頸縮,最後會斷裂。
延展性材料的頸縮和系統的幾何不穩定性有關。因為材料本身天然的不均勻,常會出現有些區域有夾雜小雜質或是出現小孔,可能是在表面或是內部,其應變會集中,讓這些區域面積比其他區域要小。在應變小於極限拉伸應變時,區域加工硬化的的應力增加率比面積縮減率要大,因此這些區域比其他區域更不容易變形,此情形下就沒有幾何不穩定性,也就是說,在極限拉伸應變之前,材料可以讓不均勻的影響降低。不過若應變繼續增加,加工硬化的效果會下降,截面較小的區域就會比其他區域要脆弱,面積減小會集中在這些區域,頸縮會越來越明顯,直到材料斷裂為止。當材料出現頸縮的情形,塑性變形會集中在頸縮部位,材料其他部份仍維持彈性變形。
延展性材料的应力-应变曲线可以用Ramberg-Osgood方程來近似[5],此方程應用上很直接,只需要材料極限拉伸強度、降伏強度、杨氏模量及伸長比例即可。
脆性材料
[编辑]
脆性材料(例如鑄鐵、玻璃及石頭等)在受到拉伸時,會在長度還沒有明顯變化時就先斷裂了[6],有些則是在降服點之前才斷裂。
像混凝土或是碳纖維之類的脆性材料沒有明確定義的降服點,也沒有應變硬化的現象,因此其最大強度等於斷裂強度。像玻璃也是脆性材料,沒有塑性變形,在彈性變形的過程中就斷裂了。這類脆性材料在拉伸變形過程沒有頸縮現象,將斷裂的二部份重新組合,形狀會和原來完全一樣。脆性材料的典型應力-應變曲線是線性的。有些材料(如混凝土)的抗拉強度遠低於拉壓強度,因此在工程應用中,會假設其抗拉強度為零。玻璃纖維的抗拉強度比鋼要大,而一整塊的玻璃無此特性,這是因為和材料中缺陷有關的应力强度因子所造成的。當試樣尺寸越大,缺陷的大小也隨之加大。一般而言,繩子的抗拉強度會小於個別纖維抗拉強度的總和。
影響因子
[编辑]不同材料的应力-应变曲线會有很大的變化,是不同內在結構及組成的結果。因為外在因素的不同,相同種類的材料進行多次的拉伸實驗,也會有不同的結果,主要會依試件的溫度以及加載的速度而不同。不過若在進一步的描,內在因素和外在因素的分界不是非常的明確。許多因素會影響应力-应变曲线,例如改變楊氏模數、硬化程度,也有可能改變結構以及其組成。
在应力-应变曲线中,常會忽略時間的影響,不過若應變率較高,其應力也會較大,其關係如下
其中的m是應變率敏感度。m越大時,材料抵抗頸縮的能力也越大。就像加工硬化係數的效果一樣
另一個主要影響因素是溫度。溫度會影響差排及擴散的活化程度。脆性材料可能會因為溫度上昇而變成延展性材料。
相關條目
[编辑]參考來源
[编辑]- ^ Luebkeman, C., & Peting, D. (2012, 04 28).
- ^ Courtney, Thomas. Mechanical behavior of materials. Waveland Press, Inc. 2005: 6–13.
- ^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 51.
- ^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 58.
- ^ Mechanical Properties of Materials. (原始内容存档于2019-05-04).
- ^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 59.


















