薄膜
薄膜材料是指厚度介于单原子到几毫米间的薄金属或有机物层。电子半导体功能器件和光学镀膜是薄膜技术的主要应用。
一个很为人们熟知的表面技术的应用是家用的镜子:为了形成反射表面在镜子的背面常常镀上一层金属,镀银操作广泛应用于镜子的制作,而低于一个纳米的极薄的镀层常常用来制作双面镜。
当光学用薄膜材料(例如减反射膜消反射膜等)由数个不同厚度不同反射率的薄层复合而成时,他们的光学性能可以得到加强。相似结构的由不同金属薄层组成的周期性排列的薄膜会形成所谓的超晶格结果。在超晶格结构中,电子的运动被限制在二维空间中而不能在三维空间中运动于是产生了量子阱效应。
薄膜技术有很广泛的应用。长久以来的研究已经将铁磁薄膜用于计算机存储设备,医药品,制造薄膜电池,染料敏化太阳能电池等。
陶瓷薄膜也有很广泛的应用。由于陶瓷材料相对的高硬度使这类薄膜可以用于保护衬底免受腐蚀氧化以及磨损的危害。在刀具上陶瓷薄膜有着尤其显著的功用,使用陶瓷薄膜的刀具的使用寿命可以有效提升几个数量级。
现阶段对于一种被称为多组分非晶重金属阳离子氧化物的新型的无机氧化物材料的研究正在进行,这种材料有望用于制造稳定,环保,低成本的透明晶体管。
沉积[编辑]
将金属薄层沉积到衬底或之前获得的薄层的技术称为表面沉积。这里的“薄”是一个相对的概念,但大多数的沉积技术都可以将薄层厚度控制在几个到几十纳米尺度的范围内,分子束外延技术可以得到单一原子层的结构。
沉积技术在光学仪器(消反射膜,减反射膜,自清洁表面等)、电子技术(薄膜电阻,半导体,集成电路)、包装和现代艺术都有应用。在对薄膜厚度要求不高时,类似于沉积的技术常常被使用。例如:用电解法提纯铜,硅沉积,铀的提纯中都用到了类似于化学气相沉积的过程。
沉积可大略分为 物理沉积(PVD)与 化学沉积(CVD)两种。
真空沉积[编辑]
- 原理
在高真空的容器中、将欲沉积的材料加热直至汽化升华、并使此气体附着于放置在附近的基板表面上、形成一层薄膜。依沉积材料、基板的种类可分为:抵抗加热、电子束、高周波诱导、雷射等加热方式。沉积材料有铝、鋅、金、银、白金、镍等金属材料与可产生光学特性薄膜的材料,主要有使用SiO2、TiO2、ZrO2、MgF2等氧化物与氟化物。沉积除金属外,树脂和树脂与玻璃也可以使用、近年来连纸也变成可沉积。
成膜时依基板与沉积材料可先使用RF等离子与离子枪照射来使沉积有更高的密着度。但是、被沉积物是树脂的时候这样做会造成反效果,因此在被沉积物的材质不明确下必须进行调查与事前的实验以免造成失败。
RF等离子加工法为真空槽内加入氩与氧气,使已经离子化的被沉积物表面变质(RF离子化)。而离子枪加工法是在离子枪内部加入氩与氧气后在离子化的基板表面设置开有φ1mm左右小孔的画素电极,而后将离子枪往该处照射进行加工(IAD:Ion Assist Deposition)
将容器真空化的作用为,沉积材料的分子在到达基板之前,避免与容器内残存的气体分子发生冲突,以及可以降低沉积材料的蒸发温度。一般需要10-3~10-4 Pa程度的真空度,要达成真空情况需使用真空泵。
沉积时的量测膜厚有使用分光学反射与折射率来计算与以水晶震动分子的沉积材料的振动数变化来测量膜厚等方法。
- 用途
光学薄膜(眼镜与镜片的反射防止膜、特殊镜子等)、磁带(录音、录像带等)、构成显示器的电极・半导体膜・绝缘膜等(电浆电视与有机EL、液晶显示器)、手机、PDA的荧幕表面・装饰表面用的涂层、电子零件(电容、半导体集积回路等)、食品包装材料(装饼干糖果用的袋子有的沉积上一层铝膜)、以至于新颖材料与建材、各式各样范围广泛接可使用此加工法。电子显微镜的标本在制作时也使用此加工法。
- 历史
1857年Michael Faraday最早提出基本原理,而后、1930年代由于油扩散式真空帮浦实用化、沉积主要用于制作镜片反射防止膜。第二次世界大战时、其他的光学机器的需求提高、真空沉积也因此快速发展。
化学沉积[编辑]
化学沉积的原理是使流体在固体基体表面发生化学变化从而在原有表面上留下了一个固体层。由于流体是环绕于固态基体的,这使得沉积可以在所有表面都发生而几乎没有方向性。即由化学沉积获得的薄膜多是均匀无方向性的。
化学沉积可以根据流体的状态进行进一步分类:
- 电镀 依靠液体,通常是金属盐在水中溶解形成的溶液,进行沉积。一些电镀过程完全靠溶液中的溶质进行(通常用于贵金属的镀层),但目前为止大多数工业上比较重要的应用均属于电极电镀。之前电镀不常用于半导体工艺中,但随着化学抛光技术的产生得到了进一步的发展。
- 化学溶液沉积(CSD)一般使用溶解有非金属有机物粉末的有机溶剂作为流体。这是一种相对简单,廉价的的用于制造满足理论计算的晶体相的沉积工艺
- 化学气相沉积(CVD) 一般使用待沉积元素的卤化物或者氢化物作为沉积源。在金属有机物化学气相沉积(MOCVD)中,金属有机物被用来作为沉积源。工业上的应用一般都使用低压高真空度的沉积气体。
- 等离子化学气相沉积(PECVD)使用离子化的蒸汽或者等离子体作为沉积源。工业应用的PECVD依靠电磁学途径(电流激励,微波激发等方式)而不是化学反应获得等离子体。
生长模式[编辑]
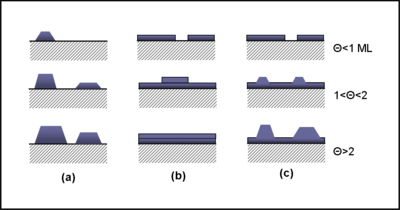
薄膜的外延生长模式(Growth Mode)被分为三大类型:岛状生长模式、层状生长模式和岛状/层状生长模式(或斯特兰斯基-克拉斯坦诺夫生长)[1]。其中,岛状生长模式又称Volmer-Weber模式、VM模式,得名于马克斯·福尔默和A. 韦伯[2]。层状生长模式又称Frank–van der Merwe模式、FM模式,得名于弗雷德里克·查尔斯·弗兰克和Jan H van der Merwe[3][4][5]。岛状/层状生长模式又称斯特兰斯基-克拉斯坦诺夫模式、SK模式,得名于伊万·斯特兰斯基和 Lyubomir Krastanov[6]。
相關條目[编辑]
参考文献[编辑]
- ^ Bauer, Ernst. Phaenomenologische Theorie der Kristallabscheidung an Oberflaechen I.. Zeitschrift für Kristallographie. 1958, 110: 372–394. Bibcode:1958ZK....110..372B. doi:10.1524/zkri.1958.110.1-6.372.
- ^ Volmer, M.; Weber, A. Keimbildung in übersättigten Gebilden. Z. Phys. Chem. 1926, 119: 277–301.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. I. Static Theory. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 205–216. Bibcode:1949RSPSA.198..205F. JSTOR 98165. doi:10.1098/rspa.1949.0095.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. II. Misfitting Monolayers and Oriented Overgrowth. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 216–225. Bibcode:1949RSPSA.198..216F. JSTOR 98166. doi:10.1098/rspa.1949.0096.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. III. Influence of the Second Harmonic Term in the Potential Representation, on the Properties of the Model. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 200 (1060): 125–134. Bibcode:1949RSPSA.200..125F. JSTOR 98394. doi:10.1098/rspa.1949.0163.
- ^ Stranski, I. N.; Krastanov, L. Zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander. Sitzungsber. Akad. Wiss. Wien. Math.-Naturwiss. 1938, 146: 797–810.
外部連結[编辑]
“薄膜在你身边”- 请和歪先生一起来了解薄膜在日常生活中有多么重要 (页面存档备份,存于互联网档案馆)
| ||||||||||||
