薄膜
薄膜材料是指厚度介於單原子到幾毫米間的薄金屬或有機物層。電子半導體功能器件和光學鍍膜是薄膜技術的主要應用。
一個很為人們熟知的表面技術的應用是家用的鏡子:為了形成反射表面在鏡子的背面常常鍍上一層金屬,鍍銀操作廣泛應用於鏡子的製作,而低於一個納米的極薄的鍍層常常用來製作雙面鏡。
當光學用薄膜材料(例如減反射膜消反射膜等)由數個不同厚度不同反射率的薄層複合而成時,他們的光學性能可以得到加強。相似結構的由不同金屬薄層組成的周期性排列的薄膜會形成所謂的超晶格結果。在超晶格結構中,電子的運動被限制在二維空間中而不能在三維空間中運動於是產生了量子阱效應。
薄膜技術有很廣泛的應用。長久以來的研究已經將鐵磁薄膜用於計算機存儲設備,醫藥品,製造薄膜電池,染料敏化太陽能電池等。
陶瓷薄膜也有很廣泛的應用。由於陶瓷材料相對的高硬度使這類薄膜可以用於保護襯底免受腐蝕氧化以及磨損的危害。在刀具上陶瓷薄膜有着尤其顯著的功用,使用陶瓷薄膜的刀具的使用壽命可以有效提升幾個數量級。
現階段對於一種被稱為多組分非晶重金屬陽離子氧化物的新型的無機氧化物材料的研究正在進行,這種材料有望用於製造穩定,環保,低成本的透明晶體管。
沉積
[編輯]將金屬薄層沉積到襯底或之前獲得的薄層的技術稱為表面沉積。這裡的「薄」是一個相對的概念,但大多數的沉積技術都可以將薄層厚度控制在幾個到幾十納米尺度的範圍內,分子束外延技術可以得到單一原子層的結構。
沉積技術在光學儀器(消反射膜,減反射膜,自清潔表面等)、電子技術(薄膜電阻,半導體,集成電路)、包裝和現代藝術都有應用。在對薄膜厚度要求不高時,類似於沉積的技術常常被使用。例如:用電解法提純銅,硅沉積,鈾的提純中都用到了類似於化學氣相沉積的過程。
沉積可大略分為 物理沉積(PVD)與 化學沉積(CVD)兩種。
真空沉積
[編輯]- 原理
在高真空的容器中、將欲沉積的材料加熱直至汽化升華、並使此氣體附着於放置在附近的基板表面上、形成一層薄膜。依沉積材料、基板的種類可分為:抵抗加熱、電子束、高周波誘導、雷射等加熱方式。沉積材料有鋁、鋅、金、銀、白金、鎳等金屬材料與可產生光學特性薄膜的材料,主要有使用SiO2、TiO2、ZrO2、MgF2等氧化物與氟化物。沉積除金屬外,樹脂和樹脂與玻璃也可以使用、近年來連紙也變成可沉積。
成膜時依基板與沉積材料可先使用RF等離子與離子槍照射來使沉積有更高的密着度。但是、被沉積物是樹脂的時候這樣做會造成反效果,因此在被沉積物的材質不明確下必須進行調查與事前的實驗以免造成失敗。
RF等離子加工法為真空槽內加入氬與氧氣,使已經離子化的被沉積物表面變質(RF離子化)。而離子槍加工法是在離子槍內部加入氬與氧氣後在離子化的基板表面設置開有φ1mm左右小孔的畫素電極,而後將離子槍往該處照射進行加工(IAD:Ion Assist Deposition)
將容器真空化的作用為,沉積材料的分子在到達基板之前,避免與容器內殘存的氣體分子發生衝突,以及可以降低沉積材料的蒸發溫度。一般需要10-3~10-4 Pa程度的真空度,要達成真空情況需使用真空泵。
沉積時的量測膜厚有使用分光學反射與折射率來計算與以水晶震動分子的沉積材料的振動數變化來測量膜厚等方法。
- 用途
光學薄膜(眼鏡與鏡片的反射防止膜、特殊鏡子等)、磁帶(錄音、錄像帶等)、構成顯示器的電極・半導體膜・絕緣膜等(電漿電視與有機EL、液晶顯示器)、手機、PDA的熒幕表面・裝飾表面用的塗層、電子零件(電容、半導體集積迴路等)、食品包裝材料(裝餅乾糖果用的袋子有的沉積上一層鋁膜)、以至於新穎材料與建材、各式各樣範圍廣泛接可使用此加工法。電子顯微鏡的標本在製作時也使用此加工法。
- 歷史
1857年Michael Faraday最早提出基本原理,而後、1930年代由於油擴散式真空幫浦實用化、沉積主要用於製作鏡片反射防止膜。第二次世界大戰時、其他的光學機器的需求提高、真空沉積也因此快速發展。
化學沉積
[編輯]化學沉積的原理是使流體在固體基體表面發生化學變化從而在原有表面上留下了一個固體層。由於流體是環繞於固態基體的,這使得沉積可以在所有表面都發生而幾乎沒有方向性。即由化學沉積獲得的薄膜多是均勻無方向性的。
化學沉積可以根據流體的狀態進行進一步分類:
- 電鍍 依靠液體,通常是金屬鹽在水中溶解形成的溶液,進行沉積。一些電鍍過程完全靠溶液中的溶質進行(通常用於貴金屬的鍍層),但目前為止大多數工業上比較重要的應用均屬於電極電鍍。之前電鍍不常用於半導體工藝中,但隨着化學拋光技術的產生得到了進一步的發展。
- 化學溶液沉積(CSD)一般使用溶解有非金屬有機物粉末的有機溶劑作為流體。這是一種相對簡單,廉價的的用於製造滿足理論計算的晶體相的沉積工藝
- 化學氣相沉積(CVD) 一般使用待沉積元素的鹵化物或者氫化物作為沉積源。在金屬有機物化學氣相沉積(MOCVD)中,金屬有機物被用來作為沉積源。工業上的應用一般都使用低壓高真空度的沉積氣體。
- 等離子化學氣相沉積(PECVD)使用離子化的蒸汽或者等離子體作為沉積源。工業應用的PECVD依靠電磁學途徑(電流激勵,微波激發等方式)而不是化學反應獲得等離子體。
生長模式
[編輯]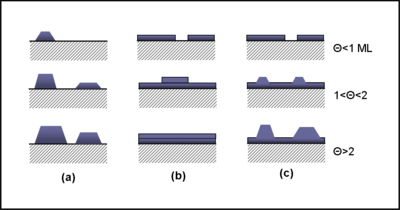
薄膜的外延生長模式(Growth Mode)被分為三大類型:島狀生長模式、層狀生長模式和島狀/層狀生長模式(或斯特蘭斯基-克拉斯坦諾夫生長)[1]。其中,島狀生長模式又稱Volmer-Weber模式、VM模式,得名於馬克斯·福爾默和A. 韋伯[2]。層狀生長模式又稱Frank–van der Merwe模式、FM模式,得名於弗雷德里克·查爾斯·弗蘭克和Jan H van der Merwe[3][4][5]。島狀/層狀生長模式又稱斯特蘭斯基-克拉斯坦諾夫模式、SK模式,得名於伊萬·斯特蘭斯基和 Lyubomir Krastanov[6]。
相關條目
[編輯]參考文獻
[編輯]- ^ Bauer, Ernst. Phaenomenologische Theorie der Kristallabscheidung an Oberflaechen I.. Zeitschrift für Kristallographie. 1958, 110: 372–394. Bibcode:1958ZK....110..372B. doi:10.1524/zkri.1958.110.1-6.372.
- ^ Volmer, M.; Weber, A. Keimbildung in übersättigten Gebilden. Z. Phys. Chem. 1926, 119: 277–301.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. I. Static Theory. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 205–216. Bibcode:1949RSPSA.198..205F. JSTOR 98165. doi:10.1098/rspa.1949.0095.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. II. Misfitting Monolayers and Oriented Overgrowth. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 216–225. Bibcode:1949RSPSA.198..216F. JSTOR 98166. doi:10.1098/rspa.1949.0096.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. III. Influence of the Second Harmonic Term in the Potential Representation, on the Properties of the Model. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 200 (1060): 125–134. Bibcode:1949RSPSA.200..125F. JSTOR 98394. doi:10.1098/rspa.1949.0163.
- ^ Stranski, I. N.; Krastanov, L. Zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander. Sitzungsber. Akad. Wiss. Wien. Math.-Naturwiss. 1938, 146: 797–810.
