S轉換 (s-transform)是一種時頻分析 的工具。
和其他時頻分析工具一樣,透過S轉換,我們可以同時從時域 以及頻域 觀察一個信號的能量分布。S轉換的特別之處在它既保持與傅立葉變換 的直接關係,又可在不同頻率有不同的解析度。此外,S轉換與小波轉換 (wavelet transform)有密切的關係,或可視為連續小波轉換 (continuous wavelet transform)的變形。S轉換的清晰度略優於加伯轉換 (Gabor transform),而不如韋格納分佈 (Wigner distribution function)、科恩克萊斯分佈 、改良式韋格納分佈 (Modified Wigner distribution function)。
一個信號x(t)的S轉換為
S
x
(
t
,
f
)
=
∫
−
∞
∞
x
(
τ
)
|
f
|
e
−
π
(
t
−
τ
)
2
f
2
e
−
j
2
π
f
τ
d
τ
{\displaystyle S_{x}(t,\,f)=\int _{-\infty }^{\infty }x(\tau )\,|f|\,e^{-\pi (t-\tau )^{2}f^{2}}e^{-j2\pi f\tau }\,d\tau }
其中窗函數 為高斯窗函數
w
(
t
,
f
)
=
|
f
|
e
−
π
t
2
f
2
{\displaystyle w(t,f)=|f|e^{-\pi t^{2}f^{2}}}
藉著摺積定理
x
(
t
)
∗
h
(
t
)
=
F
−
1
(
X
(
f
)
⋅
H
(
f
)
)
{\displaystyle x(t)\ast h(t)={\mathcal {F}}^{-1}(X(f)\cdot H(f))}
S轉換能以頻域
X
(
f
)
{\displaystyle X(f)}
S
x
(
t
,
f
)
=
∫
−
∞
∞
(
x
(
τ
)
e
−
j
2
π
f
τ
)
(
|
f
|
e
−
π
(
t
−
τ
)
2
f
2
)
d
τ
{\displaystyle S_{x}(t,f)=\int _{-\infty }^{\infty }(x(\tau )e^{-j2\pi f\tau })(|f|e^{-\pi (t-\tau )^{2}f^{2}})\,d\tau }
这里可将
S
x
(
t
,
f
)
{\displaystyle S_{x}(t,f)}
x
(
t
)
e
−
j
2
π
f
t
{\displaystyle x(t)e^{-j2\pi ft}}
|
f
|
e
−
π
t
2
f
2
{\displaystyle |f|e^{-\pi t^{2}f^{2}}}
x
(
τ
)
e
−
j
2
π
f
τ
{\displaystyle x(\tau )e^{-j2\pi f\tau }}
|
f
|
e
−
π
(
t
−
τ
)
2
f
2
{\displaystyle |f|e^{-\pi (t-\tau )^{2}f^{2}}}
傅立葉變換 可得
S
x
(
t
,
f
)
=
∫
−
∞
∞
X
(
f
+
α
)
e
−
π
α
2
/
f
2
e
j
2
π
α
t
d
α
{\displaystyle S_{x}(t,f)=\int _{-\infty }^{\infty }X(f+\alpha )\,e^{-\pi \alpha ^{2}/f^{2}}\,e^{j2\pi \alpha t}\,d\alpha }
對一訊號
x
(
t
)
{\displaystyle x(t)}
S
x
(
t
,
f
)
=
∫
−
∞
∞
x
(
τ
)
w
(
t
−
τ
,
f
)
e
−
j
2
π
f
τ
d
τ
{\displaystyle S_{x}(t,f)=\int _{-\infty }^{\infty }x(\tau )\,w(t-\tau ,f)e^{-j2\pi f\tau }\,d\tau }
其中
w
(
t
,
f
)
{\displaystyle w(t,f)}
窗函數 ,常見之窗函數為高斯函數,即
w
(
t
,
f
)
=
|
f
|
e
−
π
t
2
f
2
{\displaystyle w(t,f)=|f|e^{-\pi t^{2}f^{2}}}
事實上,S轉換之窗函數並不局限於高斯函數,考慮以下一般化型態的S轉換(generalized S transform):
S
x
(
t
,
f
,
P
)
=
∫
−
∞
∞
x
(
τ
)
w
(
t
−
τ
,
f
,
P
)
e
−
j
2
π
f
τ
d
τ
{\displaystyle S_{x}(t,f,P)=\int _{-\infty }^{\infty }x(\tau )\,w(t-\tau ,f,P)e^{-j2\pi f\tau }\,d\tau }
其中
w
(
t
,
f
,
P
)
{\displaystyle w(t,f,P)}
w
(
t
,
f
,
γ
)
=
|
f
|
e
−
π
t
2
f
2
/
γ
2
{\displaystyle w(t,f,\gamma )=|f|e^{-\pi t^{2}f^{2}/\gamma ^{2}}}
γ
{\displaystyle \gamma }
通過選取較小的
γ
{\displaystyle \gamma }
改善時頻兩域解析度的問題,可選擇非對稱的窗函數(asymmetric window),在正方向(forward direction)上有較陡峭之斜率,反方向(backward direction)上有較緩之斜率,藉由犧牲終端時間的解析度(一般而言較不重要)換取初始時間上更好的解析度。[1]
S轉換可以沿著時間軸方向積分,將可以得到
x
(
t
)
{\displaystyle x(t)}
X
(
f
)
{\displaystyle X(f)}
∫
−
∞
∞
|
f
|
e
−
π
(
t
−
τ
)
2
f
2
d
t
=
|
f
|
∫
−
∞
∞
e
−
π
(
t
−
τ
)
2
f
2
d
t
=
1
{\displaystyle \int _{-\infty }^{\infty }|f|e^{-\pi (t-\tau )^{2}f^{2}}\,dt=|f|\int _{-\infty }^{\infty }e^{-\pi (t-\tau )^{2}f^{2}}\,dt=1}
因此,沿著時間軸t積分,
∫
−
∞
∞
S
x
(
t
,
f
)
d
t
=
∫
−
∞
∞
x
(
τ
)
[
∫
−
∞
∞
|
f
|
e
−
π
(
t
−
τ
)
2
f
2
d
t
]
e
−
j
2
π
f
τ
d
τ
=
X
(
f
)
{\displaystyle \int _{-\infty }^{\infty }S_{x}(t,f)\,dt=\int _{-\infty }^{\infty }x(\tau )\left[\int _{-\infty }^{\infty }|f|\,e^{-\pi (t-\tau )^{2}f^{2}}\,dt\right]\,e^{-j2\pi f\tau }\,d\tau =X(f)}
這表示S頻譜是可逆的,同時也提供一個簡單的逆轉換。
x
(
τ
)
=
∫
−
∞
∞
[
∫
−
∞
∞
S
x
(
t
,
f
)
d
t
]
e
j
2
π
f
τ
d
f
{\displaystyle x(\tau )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }S_{x}(t,f)\,dt\right]\,e^{j2\pi f\tau }\,df}
=
∫
−
∞
∞
X
(
f
)
e
j
2
π
f
τ
d
f
{\displaystyle =\int _{-\infty }^{\infty }X(f)\,e^{j2\pi f\tau }\,df}
S轉換如同其他時頻分析轉換,皆可以設計波器來達到消除雜訊留下訊號的功用,U(t,f) ,對x(t)進行訊號處理
x
f
i
l
t
e
r
(
τ
)
=
∫
−
∞
∞
[
∫
−
∞
∞
S
x
(
t
,
f
)
⋅
U
(
t
,
f
)
d
t
]
e
j
2
π
f
τ
d
f
{\displaystyle x_{filter}(\tau )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }S_{x}(t,f)\cdot U(t,f)\,dt\right]\,e^{j2\pi f\tau }\,df}
S轉換 相較於加伯轉換 ,雖在清晰度有較好的改善,但也有其缺點,就是運算複雜度變高,積分的範圍會隨著
f
{\displaystyle f\,}
頻譜 表示式來推導離散時間S轉換
S
x
(
t
,
f
)
=
∫
−
∞
∞
X
(
f
+
α
)
e
−
π
α
2
/
f
2
e
j
2
π
α
t
d
α
{\displaystyle S_{x}(t,f)=\int _{-\infty }^{\infty }X(f+\alpha )\,e^{-\pi \alpha ^{2}/f^{2}}\,e^{j2\pi \alpha t}\,d\alpha }
令
t
=
n
Δ
T
f
=
m
Δ
F
α
=
p
Δ
F
{\displaystyle t=n\Delta _{T}\,\,f=m\Delta _{F}\,\,\alpha =p\Delta _{F}}
Δ
T
{\displaystyle \Delta _{T}\,}
,
Δ
F
{\displaystyle ,\Delta _{F}\,}
如果要使用FFT的方式來實作,必須另加條件
Δ
T
⋅
Δ
F
=
1
/
N
{\displaystyle \Delta _{T}\cdot \Delta _{F}=1/N}
首先先對
x
(
t
)
{\displaystyle x(t)}
X
(
f
)
{\displaystyle X(f)}
X
[
m
Δ
F
]
=
1
N
∑
k
=
0
N
−
1
x
[
k
Δ
T
]
e
−
j
2
π
m
k
N
{\displaystyle X[m\Delta _{F}]={\frac {1}{N}}\,\sum _{k=0}^{N-1}x[k\Delta _{T}]\,e^{\frac {-j2\pi mk}{N}}}
接著帶入頻譜表示式中,
S
x
(
n
Δ
T
,
m
Δ
F
)
=
∑
p
=
0
N
−
1
X
[
(
p
+
m
)
Δ
F
]
e
−
π
p
2
m
2
e
j
2
p
n
N
{\displaystyle S_{x}(n\Delta _{T}\,,m\Delta _{F})=\sum _{p=0}^{N-1}X[(p+m)\,\Delta _{F}]\,e^{-\pi {\frac {p^{2}}{m^{2}}}}\,e^{\frac {j2pn}{N}}}
當 m=0 時,S轉換就定義成
S
x
(
n
Δ
T
,
0
)
=
1
N
∑
k
=
0
N
−
1
x
[
k
Δ
F
{\displaystyle S_{x}(n\Delta _{T}\,,0)={\frac {1}{N}}\,\sum _{k=0}^{N-1}x[k\Delta _{F}}
Step1 : 計算
X
[
p
Δ
F
]
{\displaystyle X[p\Delta _{F}]\,}
e
−
π
p
2
m
2
{\displaystyle e^{-\pi {\frac {p^{2}}{m^{2}}}}}
f
=
m
Δ
F
{\displaystyle f=m\Delta _{F}}
X
[
p
Δ
F
]
{\displaystyle X[p\Delta _{F}]}
X
[
(
p
+
m
)
Δ
F
]
{\displaystyle X[(p+m)\Delta _{F}]}
B
[
m
,
p
]
=
X
[
(
p
+
m
)
Δ
F
]
⋅
e
−
π
p
2
m
2
{\displaystyle B[m,p]=X[(p+m)\Delta _{F}]\cdot e^{-\pi {\frac {p^{2}}{m^{2}}}}}
Step5 : 對B[m,p]取逆離散傅立葉變換 (IDFT)可得到,
S
x
(
n
Δ
T
,
m
Δ
F
)
{\displaystyle S_{x}(n\Delta _{T}\,,m\Delta _{F})}
f
=
m
Δ
F
{\displaystyle f=m\Delta _{F}}
S
x
(
n
Δ
T
,
m
Δ
F
)
{\displaystyle S_{x}(n\Delta _{T}\,,m\Delta _{F})}
S轉換與加伯轉換(Gabor Transform)很相似,
G
x
(
t
,
f
)
=
∫
−
∞
∞
x
(
τ
)
e
−
π
(
t
−
τ
)
2
e
−
j
2
π
f
τ
d
τ
{\displaystyle G_{x}(t,f)=\int _{-\infty }^{\infty }x(\tau )\,e^{-\pi (t-\tau )^{2}}e^{-j2\pi f\tau }\,d\tau }
S
x
(
t
,
f
)
=
∫
−
∞
∞
x
(
τ
)
|
f
|
e
−
π
(
t
−
τ
)
2
f
2
e
−
j
2
π
f
τ
d
τ
{\displaystyle S_{x}(t,f)=\int _{-\infty }^{\infty }x(\tau )\,|f|e^{-\pi (t-\tau )^{2}f^{2}}e^{-j2\pi f\tau }\,d\tau }
唯一的不同就在於S轉換的Gaussian Window的寬度會隨著
f
{\displaystyle f}
低頻
時域解析度差
頻域解析度佳
高頻
頻域解析度差
時域解析度佳
原因就是
f
{\displaystyle f\,}
f
{\displaystyle f\,}
f
→
0
{\displaystyle f\rightarrow 0}
f
2
{\displaystyle f^{2}\,}
S轉換一般式
S
x
(
t
,
f
)
=
|
s
(
f
)
|
∫
−
∞
∞
x
(
τ
)
e
−
π
(
t
−
τ
)
2
s
2
(
f
)
e
−
j
2
π
f
τ
d
τ
{\displaystyle S_{x}(t,f)=|s(f)|\int _{-\infty }^{\infty }x(\tau )\,e^{-\pi (t-\tau )^{2}s^{2}(f)}e^{-j2\pi f\tau }\,d\tau }
s
(
f
)
{\displaystyle s(f)}
f
→
0
{\displaystyle f\rightarrow 0}
s
(
f
)
≠
0
{\displaystyle s(f)\neq 0}
S轉換是一種運算量高的時頻分析工具,尤其在低頻部分,Gaussian Window寬度變寬,頻域解析度比加伯轉換來的好,所以S轉換對於低頻訊號分析比較有優勢
韋格納分佈是時頻分析工具中,具有高清晰度的一個,但最大的缺點是有交叉項(cross-term)的問題。若一個信號是由數個信號成份組合而成,那麼使用韋格納分佈來分析時就會受到兩兩信號成份之間的交叉項干擾,这将会产生一些不必要的噪声。一個信號x的韋格納分佈為
W
x
(
t
,
f
)
=
∫
−
∞
∞
x
(
t
+
τ
2
)
x
∗
(
t
−
τ
2
)
e
−
j
2
π
τ
f
d
τ
{\displaystyle W_{x}(t,f)=\int _{-\infty }^{\infty }x(t+{\frac {\tau }{2}})x^{*}(t-{\frac {\tau }{2}})e^{-j2\pi \tau f}\,d\tau }
交叉項是在積分中兩個x項相乘時產生的。S轉換的計算原理與韋格納分佈不同,是直接對
x
(
τ
)
{\displaystyle x(\tau )}
加伯轉換的定義為
G
x
(
t
,
f
)
=
∫
−
∞
∞
x
(
τ
)
e
[
−
π
(
t
−
τ
)
2
f
2
]
e
(
−
j
2
π
f
τ
)
d
τ
{\displaystyle G_{x}(t,f)=\int _{-\infty }^{\infty }x(\tau )e^{\left[-\pi (t-\tau )^{2}f^{2}\right]}e^{\left(-j2\pi f\tau \right)}d\tau }
我們知道加伯轉換是短時距傅立葉轉換的一種特殊形式,其中只要把短時距傅立葉轉換的窗函數用高斯函數來替代就成了加伯轉換;S轉換則可視為一種窗函數會隨f變化的加伯轉換;隨著頻率的升高,高斯函數在時域上的寬度會越來越窄,使得時域上的解析度會增加,反之犧牲頻域上的解析度。
加伯轉換和S轉換原理相同,兩者唯一不同的地方就是窗函數的
f
2
{\displaystyle f^{2}}
f
{\displaystyle f}
連續小波轉換可以視為將一個信號對小波做相關 (correlation):
W
(
τ
,
d
)
=
∫
−
∞
∞
x
(
t
)
W
(
t
−
τ
,
d
)
d
t
{\displaystyle W(\tau ,\,d)=\int _{-\infty }^{\infty }x(t)\,W(t-\tau ,\,d)\,dt}
而S轉換可以視為連續小波轉換乘上一個相位項:
S
(
τ
,
f
)
=
e
−
j
2
π
τ
f
W
(
τ
,
d
)
{\displaystyle S(\tau ,\,f)=e^{-j2\pi \tau f}W(\tau ,\,d)}
而其用的母小波為:
w
(
t
,
f
)
=
|
f
|
exp
[
−
π
t
2
f
2
]
exp
[
−
j
2
π
f
t
]
{\displaystyle w(t,\,f)=|f|\,\exp[-\pi t^{2}f^{2}]\exp[-j2\pi ft]}
假設我們想要對一訊號
x
(
t
)
{\displaystyle x(t)}
x
(
t
)
=
c
o
s
(
2
π
t
)
,
t
<
10
,
{\displaystyle x(t)=cos(2\pi t),t<10,}
x
(
t
)
=
c
o
s
(
2
π
t
)
,
10
≤
t
<
20
,
{\displaystyle x(t)=cos(2\pi t),10\leq t<20,}
x
(
t
)
=
c
o
s
(
2
π
t
)
,
20
≤
t
.
{\displaystyle x(t)=cos(2\pi t),20\leq t.}
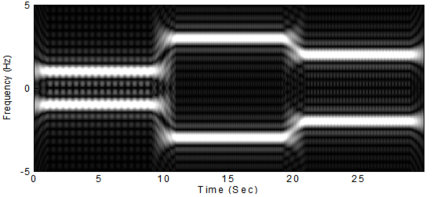
如果使用一個寬度為1秒的矩形函數來做短時距傅立葉轉換會得到
如果使用一個加伯轉換會得到時頻分析圖
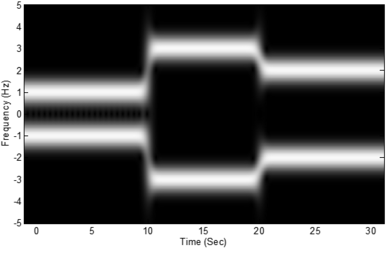
如果用S轉換會得到時頻分析圖
由上三圖可知,S轉換是一個在低頻時頻域解析度高,高頻時時域解析度高的時頻分析;舉例來說,對於100Hz與300Hz和1000Hz與1200Hz這兩組聲音,哪一組對於人耳會有明顯的差異呢? 答案是100Hz和300Hz,低頻時的頻率差異對於人耳較明顯,當頻率越高時,人耳就越難分辨出頻率的差異;同樣的道理,S轉換便符合我們的需求,低頻時訊號變化慢擁有低的時域解析度和擁有高的頻域解析度,高頻時因為訊號變化很快則擁有高的時域解析度和低的頻域解析度。
R. G. Stockwell, L. Mansinha, and R. P. Lowe, "Localization of the complex spectrum: the S transform," IEEE Trans. Signal Processing, vol. 44, no. 4, pp. 998–1001, Apr. 1996.
Jian-Jiun Ding, Time frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2010.
Sitanshu Sekhar, Ganapati Panda and Nithin V George, "An Improved S-Transform for Time-Frequency Analysis," "IACC2009", pp. 315-319, March 2009.
^ The S-transform with windows of arbitrary and varying shape, C. Robert Pinnegar, Lalu Mansinha, GEOPHYSICS, VOL.68, NO.1 (JANUARY-FEBRUARY 2003); P.381–385






















![{\displaystyle \int _{-\infty }^{\infty }S_{x}(t,f)\,dt=\int _{-\infty }^{\infty }x(\tau )\left[\int _{-\infty }^{\infty }|f|\,e^{-\pi (t-\tau )^{2}f^{2}}\,dt\right]\,e^{-j2\pi f\tau }\,d\tau =X(f)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14e6b352156da8033cca125003140df358d3c297)
![{\displaystyle x(\tau )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }S_{x}(t,f)\,dt\right]\,e^{j2\pi f\tau }\,df}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2af5491d487dc8fae81d248ffb805c4846c41b8)

![{\displaystyle x_{filter}(\tau )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }S_{x}(t,f)\cdot U(t,f)\,dt\right]\,e^{j2\pi f\tau }\,df}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b60fa32f66dcd95e2178f3bef55e8581f62e9320)





![{\displaystyle X[m\Delta _{F}]={\frac {1}{N}}\,\sum _{k=0}^{N-1}x[k\Delta _{T}]\,e^{\frac {-j2\pi mk}{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/498f32de39c38e3e1c43aadcdaad4a555ff67941)
![{\displaystyle S_{x}(n\Delta _{T}\,,m\Delta _{F})=\sum _{p=0}^{N-1}X[(p+m)\,\Delta _{F}]\,e^{-\pi {\frac {p^{2}}{m^{2}}}}\,e^{\frac {j2pn}{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/219978e25a5bbd799c343a7b3be9786d3e9a3494)

![{\displaystyle X[p\Delta _{F}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36dc23f645fa9c4ac7fdd712619ce6ddb514620d)


![{\displaystyle X[p\Delta _{F}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbc38aa030d987c1378f08c0e4e3f9d32fa285fd)
![{\displaystyle X[(p+m)\Delta _{F}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff9be139c342d944a9e1caba1b5b46fe2750a17)
![{\displaystyle B[m,p]=X[(p+m)\Delta _{F}]\cdot e^{-\pi {\frac {p^{2}}{m^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee8d284c8a44c574c591f6556f95a08008277a54)











![{\displaystyle G_{x}(t,f)=\int _{-\infty }^{\infty }x(\tau )e^{\left[-\pi (t-\tau )^{2}f^{2}\right]}e^{\left(-j2\pi f\tau \right)}d\tau }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f249ce95c32b3b23438166c47f67b5b15fe0fbf)



![{\displaystyle w(t,\,f)=|f|\,\exp[-\pi t^{2}f^{2}]\exp[-j2\pi ft]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7047d506ef8d68712088aa3a74a3052f36b3a78d)


