跳转到内容

立方五角十二面體

编辑链接
本页使用了标题或全文手工转换
维基百科，自由的百科全书
立方五角十二面體
立方五角十二面體
類別凸多面體
名稱立方五角十二面體
切稜五角十二面体 （日語）
Würfel-Pentagondodekaeder （德語）
性質
面18
邊48
頂點32
歐拉特徵數F=18, E=48, V=32 （χ=2）
組成與佈局
面的種類6個矩形
12個不等邊六邊形
對稱性
對稱群Th, [4,3+], (3*2)[1]
特性
凸

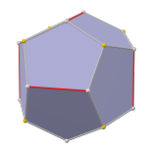
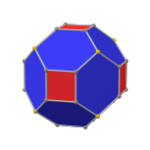
在幾何學中，立方五角十二面體（德文：Würfel-Pentagondodekaeder[2]）是一種由6個矩形和12個不等邊六邊形組成的十八面體，具有五角十二面體群對稱性。這種立體可以透過將立方體的6個面的每個面分割成3個矩形，並且相鄰面方向互相垂直的結構變形而來，其對應的球面鑲嵌結構通常用於傳統的排球上。[3][4]部分的礦物可以結晶成這種形狀，例如部分的黄铁矿。[5]

性質

[编辑]

立方五角十二面體共由18個面、48條邊和32個頂點組成，其具有五角十二面體群對稱性，或稱為Th群，這種對稱性被認為與傳統的排球相同[6]。在這個幾何結構的18個面中，有6個矩形和12個不等邊六邊形。在其48條邊中，有12條邊等長的較長邊和36條較短的等長邊。其32個頂點也可以分為兩種，一種為2個六邊形和一個矩形的公共頂點，這種頂點有24個，其餘6個為3個六邊形的公共頂點。

對稱性

[编辑]

立方五角十二面體具有五角十二面體群對稱性，或稱為Th群，這種對稱群具有與四面體群相同的旋轉對稱軸以及平行於立方體面的鏡射對稱面[5]，並且與A4 × Z2對稱性同構[6]，同時，球面化的排球也保持著這種對稱性，[7][8]且皆為24階對稱性。[9]

結構

[编辑]

立方五角十二面體可以透過將五角十二面體的6條長邊截去來構造[10]。其也可以透過將倒角立方體的正方形面拉長成矩形，並且使鄰近的矩形皆朝不同的方向拉長來構造，因此立方五角十二面體的拓樸結構與倒角立方體同構。[11]

使用

[编辑]

球面化後的立方五角十二面體其六邊形面可以視為球面矩形，因此整體形狀可以視為6組每組3個的矩形在球面上形成的球面鑲嵌[註 1]，這種立體結構通常用於排球及早期的足球[3][12]，然而現今的足球更常用的形狀是球面化的截角二十面體。在晶體學中，部分的黄铁矿會形成平面的立方五角十二面體形狀的結晶體[13][14]。

相關多面體

[编辑]

立方五角十二面體在晶體學中通常會被視為是立方晶體與五角十二面晶體的組合[15]，即密勒指數為{100}和{210}晶體結構的組合[16]。而在數學中立方五角十二面體可透過將五角十二面體截去其中6個稜來構造，因此在部分文獻中，立方五角十二面體又稱為截六稜五角十二面體（英語：Chamfered 6 pyritohedron[17]），在日語中，立方五角十二面體又稱為切棱五角十二面體（切稜五角十二面体）[18]。

立方五角十二面體與倒角立方體的拓樸結構等價。立方五角十二面體可以看做是從立方體漸進形變到倒角立方體的一個中間體。 [19]同時立方五角十二面體也可以視為特殊的切稜立方體，其可以透過切角小於45度且深度大於零的方式切去立方體的稜來構造[18]。

立方五角十二面體可以透過將立方體6個面的每個面分割成3個矩形，並且相鄰面方向互相垂直的結構變形而來，而將立方體面分割成不同數量的矩形可以形成不同的結果，例如每個面皆分割成2個矩形可以形成五角十二面體[20]。

分割數 1 2 3 4 5
圖像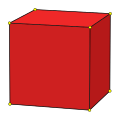
球面鑲嵌
幾何結構 立方體 五角十二面體 立方五角十二面體 一種球面鑲嵌[21] 一種十分罕見的礦石晶形，

曾於腓特烈港發現。[22]

參見

[编辑]

註釋

[编辑]
  1. ^ 一個多面體的球面鑲嵌或球面多面體是指將該多面體投影到球面上所形成的幾何結構。

參考文獻

[编辑]
  1. ^ Leonard R. MacGillivray, Jerry L. Atwood. Ehud Keinan, Israel Schechter , 编. Spherical Molecular Assemblies: A Class of Hosts for the Next Millennium. Weinheim, Germany: Wiley-VCH Verlag GmbH. 2000-12-20: 130–150 [2021-09-10]. ISBN 9783527612949. doi:10.1002/9783527612949.ch09. （原始内容存档于2021-09-10） （英语）. 
  2. ^ Modelle, Kristallform Würfel-Pentagondodekaeder [Krantz 379, 380]. Gesellschaft für Universitätssammlungen e.V. [2019-11-04]. （原始内容存档于2019-10-10）. 
  3. ^ 3.0 3.1 Paul Bourke, § Volley ball (Gaelic football, Water polo, Netball), Geometry of sports balls, Paul Bourke, January 2017 [2019-10-10], （原始内容存档于2018-07-27） 
  4. ^ Karimi, Alireza and Kudo, Susumu and Razaghi, Reza and Navidbakhsh, Mahdi. Measurement of the mechanical properties of the handball, volleyball, and basketball using DIC method: a combination of experimental, constitutive, and viscoelastic models. Sport Sciences for Health (Springer). 2015, 11 (3): 295––303. 
  5. ^ 5.0 5.1 Daniel Arovas. Crystal Math (PDF). 聖地牙哥加利福尼亞大學. 2018 [2019-11-04]. （原始内容 (PDF)存档于2019-10-10）. 
  6. ^ 6.0 6.1 Sattler, K.D. Handbook of Nanophysics: Clusters and Fullerenes. Handbook of Nanophysics. CRC Press. 2010: 28.4. ISBN 9781420075557. LCCN 2009047135. 
  7. ^ Stanislav Jendrol, František Kardoš, Symmetry of fulleroids (PDF), Sep, 2010 [2019-11-04], （原始内容 (PDF)存档于2019-10-10） 
  8. ^ Bromley, S.T. and Woodley, S.M. Computational Modelling of Nanoparticles. Frontiers of Nanoscience. Elsevier Science. 2018: p.195. ISBN 9780081022757. 
  9. ^ Michael Engel, Ann Arbor, Part 1: Point symmetry, Short‐course on symmetry and crystallography, Center for Assembly Science & Engineering, University of Michigan, June, 2011 
  10. ^ William E. Ford. Cube and pyritohedron. usf.edu. 1912 [2021-08-15]. （原始内容存档于2021-08-15）. 
  11. ^ §The Chamfered Cube and the Dodecahedron, Article 47: Geometry - Platonic Solids - Part 8 - The Cube. Cosmic Core. [2019-11-06]. （原始内容存档于2019-11-06）. 
  12. ^ Swart, David; et al, Soccer Ball Symmetry, Proceedings of Bridges 2015: Mathematics, Music, Art, Architecture, Culture (Tessellations Publishing), 2015: 151––158 
  13. ^ Matthes, Siegfried. Mineralogie: Eine Einführung in die spezielle Mineralogie, Petrologie und Lagerstättenkunde. Springer Berlin Heidelberg. 2013: p.43. ISBN 9783662087695. 
  14. ^ Baur, Ludwig. Kurzes Lehrbuch der Mineralogie und Geologie. Aischines Verlag. 2015: p.62. ISBN 9783738792621. 
  15. ^ Crystal shapes. The Australian Museum. [2019-10-10]. （原始内容存档于2019-03-31）. 
  16. ^ Susanne Herting-Agthe. Pyrite, striated cubes. mineralogische-sammlungen.de. 2009 [2021-08-15]. （原始内容存档于2022-05-11）. 
  17. ^ Watchduck. Convex polyhedra, a python program to generate Convex polyhedra, polyhedron_properties.py. GitHub. 
  18. ^ 18.0 18.1 多面体木工. 特定非営利活動法人 科学協力学際センター. 2006/8/1. 
  19. ^ chamfered cube. bendwavy.org. [2019-11-04]. （原始内容存档于2021-09-30）. 
  20. ^ Koca, Nazife O and Al-Mukhaini, Aida Y and Koca, Mehmet and Al-Qanobi, Amal J. Symmetry of the pyritohedron and lattices. Sultan Qaboos University Journal for Science [SQUJS]. 2016, 21 (2): 139––149. 
  21. ^ Hyde, Stephen T. Contemporary Geometry For The Built Design?. Architectural Theory Review (Taylor & Francis). 2010, 15 (2): 110––124. 
  22. ^ Donald Peck, Alfred Ostrander. Crystallography: The Isometric System. 2019-10-20 [2019-11-06]. （原始内容存档于2019-11-06）. 
检索自“https://zh.wikipedia.org/w/index.php?title=立方五角十二面體&oldid=75153188”