粉紅雜訊

粉紅噪聲或1/ƒ噪音（有時也稱作閃爍雜訊）是一個具有功率譜密度（能量或功率每赫茲）與頻率成反比特徵頻譜的信號或過程。在粉紅噪聲中，每個倍頻程中都有一個等量的噪聲功率。粉紅噪聲的名稱源於這種功率譜下的可見光視覺顏色為粉色。

在科學文獻中，術語1/ƒ 噪聲通常寬泛地指任何一種帶有如下所示功率譜密度的噪聲：

$S(f)\propto 1/f^{\alpha }$

其中ƒ為頻率，且0 < α < 2，α一般趨近於1。形如1/ƒ^α的噪聲廣泛地存在於大自然之中，並且它被運用到許多領域當中。α 值趨近於1的噪聲與區間內其它α值噪聲之間的區別符合一個更基本的區別。前者（狹義上）一般來自於准平衡凝聚態系統，下文將會展開討論。後者（廣義上）一般符合一系列非均衡驅動動態系統。

儘管術語閃變噪聲僅用來描述直流電子設備中出現的噪聲更為合適，但每當提到1/ƒ噪聲人們還是稱其為閃變噪聲。1968年，本華·曼德博與John W. Van Ness提出了一個「分數噪聲」的概念（有時也叫做分形噪聲），以強調譜函數的指數可取一個非整數值，並使之與分數布朗運動聯繫起來，但這個詞很少被用到。

描述

粉紅噪聲的近似功率譜。功率密度以10 dB每十倍頻程衰減。

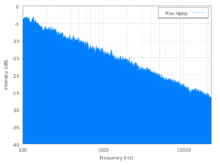
粉紅噪聲在所有倍頻程（或對數坐標）內都有相同能量。在有限頻寬內，1/ƒ噪聲以3 dB每倍頻程衰減，因此在高頻段就不會有1/ƒ噪聲出現。（而白噪聲在每赫茲上都有相同能量。）

粉紅噪聲（左）和白噪聲（右）在FFT頻譜圖上，縱軸為由下向上線性增加的頻率軸。（在音頻或類似的頻譜分析軟件中，粉紅噪聲為平滑曲線而不是斜率下降的曲線，白噪聲表現為斜率上升。）

人類的聽覺系統，其處理頻率的原理大致為由Bark scale給出的對數形式，即對於不同頻率的敏感度並不相同。處在2–4-kHz倍頻程的信號聽上去最大，而其他頻段的響度感覺則急劇下降，這取決於與高敏感度頻域的距離和聲級。儘管如此，人類依然能輕易地分辨出白噪聲與粉紅噪聲。

圖形均衡器將信號分為不同的對數帶寬並以八度顯示能量。音頻工程師將粉紅噪聲輸入系統以測試其在給定功率譜下是否能輸出平坦響應。無法得到平坦響應的系統可以通過圖形均衡器的均衡化從而得到一個鏡像。因為粉紅噪聲在自然界物理系統中發生，所以它被廣泛應用在音頻產品當中。粉紅噪聲可以被處理、濾波或生成期望的聲音效果。粉紅噪聲的商用產品是粉紅噪聲發生器。

從實際應用來看，生成一個真正意味的粉紅噪聲是不可能的，因為假如存在真正的粉紅噪聲，其功率將會是無窮大的。這是說，粉紅噪聲在從ƒ₁到ƒ₂的任意頻率區間內的能量都正比於log(ƒ₂/ƒ₁)，那麼根據粉紅噪聲的定義，如果ƒ₂為無窮大，能量也將會變得無窮大。同樣地，當ƒ₁ = 0時，粉紅噪聲的能量是無窮大的。

因此事實上，粉紅噪聲只能表現為有限頻率範圍內的噪聲。定義其頻響區間為ƒ₁為下限頻率、ƒ₂為其上限頻率。

噪聲的一個屬性，峰值因數即峰值比上平均功率，對於測試如放大器和揚聲器等設備的能力來說是很重要的一個特性。不同峰值因數的粉紅噪聲可用來模擬不同等級動態範圍壓縮的音樂信號。一個給定的峰值因數對於功率放大器或揚聲器的耐久性或發熱測試來說也很重要。因為信號的功率是關於峰值因數的直接函數。一些商用數字式粉紅噪聲發生器可以定製峰值係數，因為公式自身的特性可以確保信號不觸發某一特定電平。

維度廣義化

粉紅噪聲的譜函數相關於1/f只限於一維度信號。而對於二維度信號，例如圖像，譜函數則是f²的倒數。一般的，在n維度系統中，譜函數則是fⁿ的倒數。對於更高維度的信號來說，每個倍頻程帶中都有等量噪聲功率的特性仍然成立。因此二維信號的頻譜也是二維的，而其倍頻程的面積則是之前的四倍。

粉紅噪聲現象

1/ƒ噪聲發生在很多物理、生物乃至經濟系統當中。一些研究者稱它為無所不在。在物理系統中，它往往被應用在氣象數據分析、天體輸出的電磁輻射、和大部分的電子設備當中（即閃變噪聲）。在生物系統當中，它被應用在心律分析、神經系統活動、DNA序列統計分析當中。在金融系統中，它常與「長期記憶效應」相聯繫。並且1/ƒ噪聲也可作為許多自然圖片（來自於自然環境的圖片）統計結構的表現形式。 最近，1/ƒ噪聲也被成功地應用於心理學的精神狀態建模當中。

Richard F. Voss 和 J. Clarke聲稱幾乎全部的音樂旋律，將每一段連續的音符繪製於一個橫軸為音高的圖中，將會趨於一個粉紅噪聲頻譜。 與這種研究方法相似的是，康奈爾大學的科研人員James E. Cutting，通過對1935至2005年間發行的150部熱門電影的研究發現，鏡頭時長形成一個1/f的統計學分布圖樣。

雖然通過自組織臨界性已經可以在沙盤中生成1/f噪聲，但仍沒有一個簡單的數學模型能夠生成粉紅噪聲。粉紅噪聲通常對白噪聲進行濾波生成。

關於1/ƒ噪聲本體已有很多理論。部分是通用理論，而其他理論則僅局限於特定材料，比如半導體。1/ƒ噪聲的通用理論研究為目前的學術界興趣所在。

電子設備

主條目：閃變噪聲

本領域內的先驅者是科研人員Aldert van der Ziel。

在電子設備中，白噪聲在某些截止頻率處表現得比粉紅噪聲（或閃變噪聲）要更強。目前無法探知粉紅噪聲的下限頻率，即使將測量設備的測試對象頻率降到10⁻⁶ Hz附近（這往往需要幾周時間）仍然會有粉紅噪聲的現象出現。

有些模擬合成器會包含一個粉紅噪聲源（儘管白噪聲源更加普遍），二者在後續的處理當中均可作為一個有用標準音頻聲源，或作為一個控制其他合成器的隨機控制電壓。

電子設備中的1/f噪聲源主要來自其中凝聚態材料部件的慢波動屬性。在大多情況下，這種波動源是已知的。不同的波動形式來自於金屬缺陷，半導體材料陷阱作用中的波動占有率，磁性材料中的波動域結構等。 對於類1/f頻譜公式的解釋通常比較多，這取決於波動過程的動力學活化能統計分布。因為大部分噪聲實驗設備的頻響範圍（如1 Hz–1 kHz）一般要低於微觀的「試圖逃逸」頻率（如10¹⁴ Hz），所以阿倫尼烏斯方程中的指數因子對於公式的權重很大。這些部分活化能擴散範圍相對較小從而得到特徵率的擴散範圍更大。對於一個最簡單的電子玩具，其動力學活化能的平坦分布形成一個類1/f頻譜，因為${\frac {\mathrm {d} \ln f}{\mathrm {d} f}}={\frac {1}{f}}$。

內部連結

• 白噪聲
• 噪聲的顏色
• 峰值係數
• 統計學

參考文獻

• Bak, P. and Tang, C. and Wiesenfeld, K. Self-Organized Criticality: An Explanation of 1/ƒ Noise. Physical Review Letters. 1987, 59 (4): 381–384. Bibcode:1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381. 
• Dutta, P. and Horn, P. M. Low-frequency fluctuations in solids: 1/ƒ noise. Reviews of Modern Physics. 1981, 53 (3): 497–516. Bibcode:1981RvMP...53..497D. doi:10.1103/RevModPhys.53.497. 
• Field, D. J. Relations Between the Statistics of Natural Images and the Response Profiles of Cortical Cells (PDF). Journal of the Optical Society of America A. 1987, 4 (12): 2379–2394 [2012-03-24]. Bibcode:1987JOSAA...4.2379F. PMID 3430225. doi:10.1364/JOSAA.4.002379. （原始內容存檔 (PDF)於2021-04-13）. 
• Gisiger, T. Scale invariance in biology: coincidence or footprint of a universal mechanism?. Biological Reviews. 2001, 76 (2): 161–209. doi:10.1017/S1464793101005607. 
• Johnson, J. B. The Schottky effect in low frequency circuits. Physical Review. 1925, 26: 71–85. Bibcode:1925PhRv...26...71J. doi:10.1103/PhysRev.26.71. 

• Kogan, Shulim. Electronic Noise and Fluctuations in Solids. [Cambridge University Press]. 1996. ISBN 0-521-46034-4. 

• Press, W. H. Flicker noises in astronomy and elsewhere (PDF). Comments on Astrophysics. 1978, 7: 103–119 [2012-03-24]. Bibcode:1978ComAp...7..103P. （原始內容存檔 (PDF)於2021-02-13）. 
• Schottky, W. Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern. Annalen der Physik. 1918, 362 (23): 541–567. Bibcode:1918AnP...362..541S. doi:10.1002/andp.19183622304. 
• Schottky, W. Zur Berechnung und Beurteilung des Schroteffektes. Annalen der Physik. 1922, 373 (10): 157–176. Bibcode:1922AnP...373..157S. doi:10.1002/andp.19223731007. 
• Keshner, M. S. 1/ƒ noise. Proceedings of the IEEE. 1982, 70 (3): 212–218. doi:10.1109/PROC.1982.12282. 
• Li, W. A bibliography on 1/ƒ noise. 1996–present [2012-03-24]. （原始內容存檔於2004-02-08）. 
• Mandelbrot, B. B. and Van Ness, J. W. Fractional Brownian motions, fractional noises and applications. SIAM Review. 1968, 10 (4): 422–437. Bibcode:1968SIAMR..10..422M. doi:10.1137/1010093. 
• A. Chorti and M. Brookes (2007), "Resolving near-carrier spectral infinities due to 1/ƒ phase noise in oscillators", ICASSP 2007, Vol. 3, 15–20 April 2007, Pages:III–1005 — III–1008, DOI 10.1109/ICASSP.2007.366852

外部連結

• Powernoise: Matlab software for generating 1/ƒ noise, or more generally, 1/ƒ^α noise （頁面存檔備份，存於網際網路檔案館）
• A Bibliography on 1/ƒ Noise
• 1/f noise at Scholarpedia （頁面存檔備份，存於網際網路檔案館）