坐標下降法
外觀
坐標下降法(英語:coordinate descent)是一種非梯度優化算法。算法在每次迭代中,在當前點處沿一個坐標方向進行一維搜索以求得一個函數的局部極小值。在整個過程中循環使用不同的坐標方向。對於不可拆分的函數而言,算法可能無法在較小的迭代步數中求得最優解。為了加速收斂,可以採用一個適當的坐標系,例如通過主成分分析獲得一個坐標間儘可能不相互關聯的新坐標系(參考自適應坐標下降法)。
算法描述
[編輯]坐標下降法基於的思想是多變量函數可以通過每次沿一個方向優化來獲取最小值。與通過梯度獲取最速下降的方向不同,在坐標下降法中,優化方向從算法一開始就予以固定。例如,可以選擇線性空間的一組基作為搜索方向。 在算法中,循環最小化各個坐標方向上的目標函數值。亦即,如果已給定,那麼,的第個維度為
因而,從一個初始的猜測值以求得函數的局部最優值,可以迭代獲得的序列。
通過在每一次迭代中採用一維搜索,可以很自然地獲得不等式
可以知道,這一序列與最速下降具有類似的收斂性質。如果在某次迭代中,函數得不到優化,說明一個駐點已經達到。
這一過程可以用下圖表示。
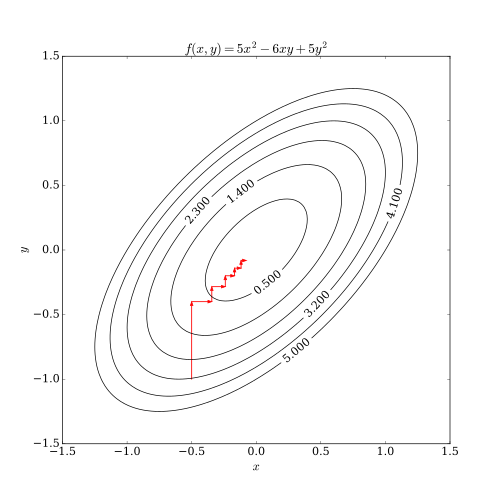
例子
[編輯]對於非平滑函數,坐標下降法可能會遇到問題。下圖展示了當函數等高線非平滑時,算法可能在非駐點中斷執行。
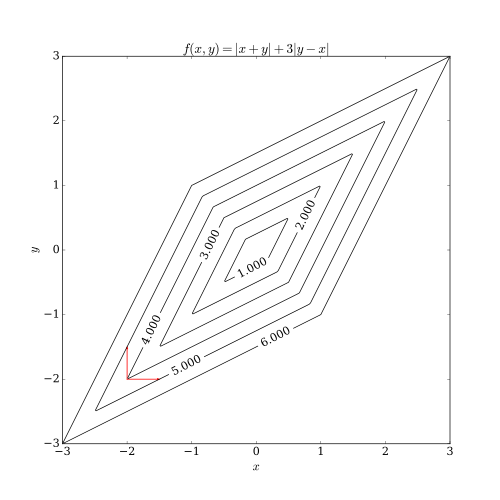
應用
[編輯]坐標下降法在機器學習中有應用,例如訓練線性支持向量機[1](可見LIBLINEAR)以及非負矩陣分解[2]。
參見
[編輯]參考
[編輯]- ^ Cho-Jui Hsieh, Kai-Wei Chang, Chih-Jen Lin, S. Sathiya Keerthi, S. Sundararajan. A dual coordinate descent method for large-scale linear SVM. ACM: 408–415. 2008-07-05 [2018-04-02]. ISBN 9781605582054. doi:10.1145/1390156.1390208.
- ^ Cho-Jui Hsieh, Inderjit S. Dhillon. Fast coordinate descent methods with variable selection for non-negative matrix factorization. ACM: 1064–1072. 2011-08-21 [2018-04-02]. ISBN 9781450308137. doi:10.1145/2020408.2020577.
- Bezdek, J. C.; Hathaway, R. J.; Howard, R. E.; Wilson, C. A.; Windham, M. P., Local convergence analysis of a grouped variable version of coordinate descent, Journal of Optimization theory and applications 54 (3) (Kluwer Academic/Plenum Publishers), 1987, 54 (3): 471–477, doi:10.1007/BF00940196
- Bertsekas, Dimitri P. (1999). Nonlinear Programming, Second Edition Athena Scientific, Belmont, Massachusetts. ISBN 1-886529-00-0.
- Canutescu, AA; Dunbrack, RL, Cyclic coordinate descent: A robotics algorithm for protein loop closure., Protein science 12 (5), 2003, 12 (5): 963–72, PMID 12717019.
- Luo, Zhiquan; Tseng, P., On the convergence of the coordinate descent method for convex differentiable minimization, Journal of Optimization theory and applications 72 (1) (Kluwer Academic/Plenum Publishers), 1992, 72 (1): 7–35, doi:10.1007/BF00939948.
- Wu, TongTong; Lange, Kenneth, Coordinate descent algorithms for Lasso penalized regression, The Annals of Applied Statistics 2 (1) (Institute of Mathematical Statistics), 2008, 2 (1): 224–244, doi:10.1214/07-AOAS147.
- Richtarik, Peter; Takac, Martin, Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function, Mathematical Programming (Springer), April 2011, doi:10.1007/s10107-012-0614-z.
- Richtarik, Peter; Takac, Martin, Parallel coordinate descent methods for big data optimization, arXiv:1212.0873, December 2012.










